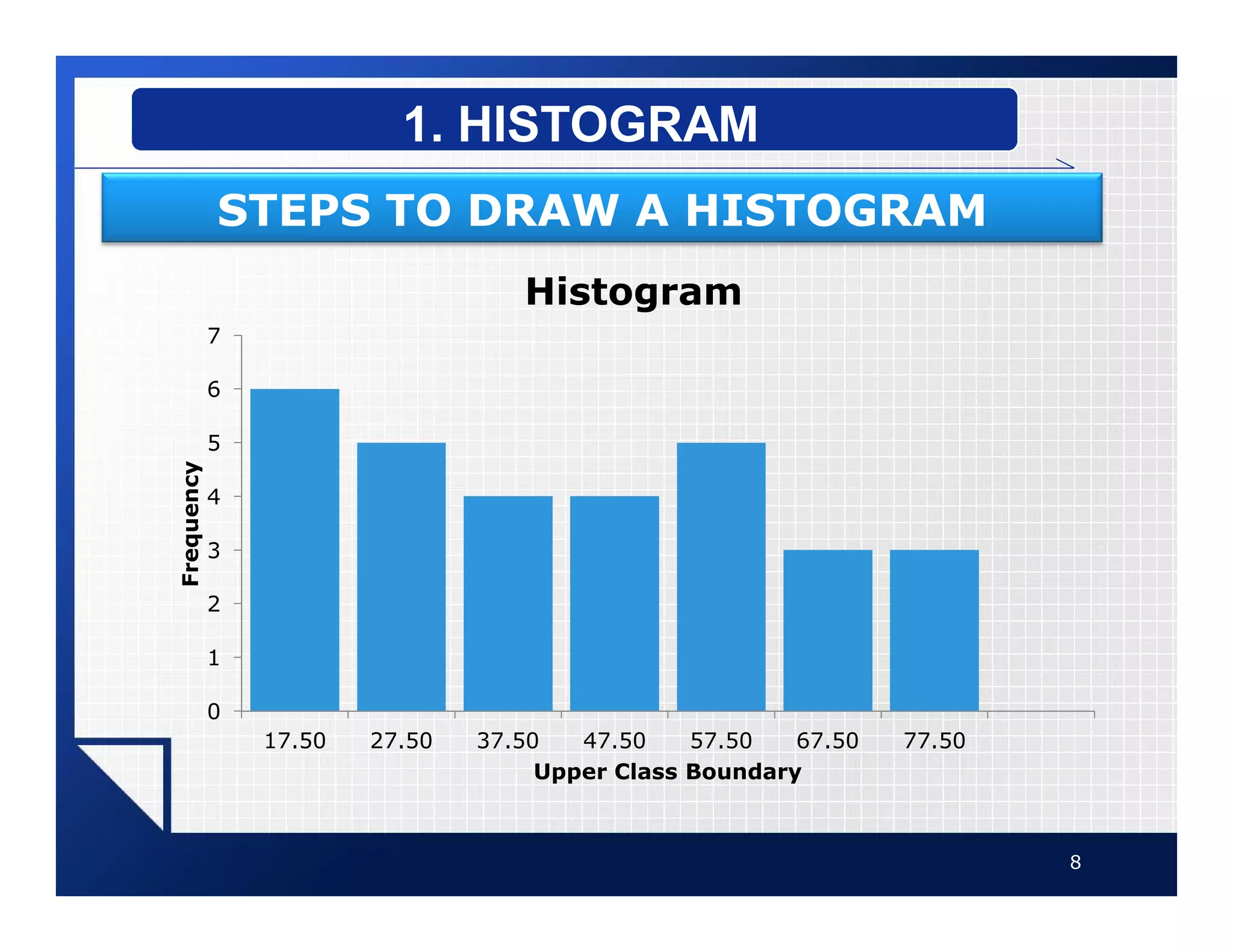
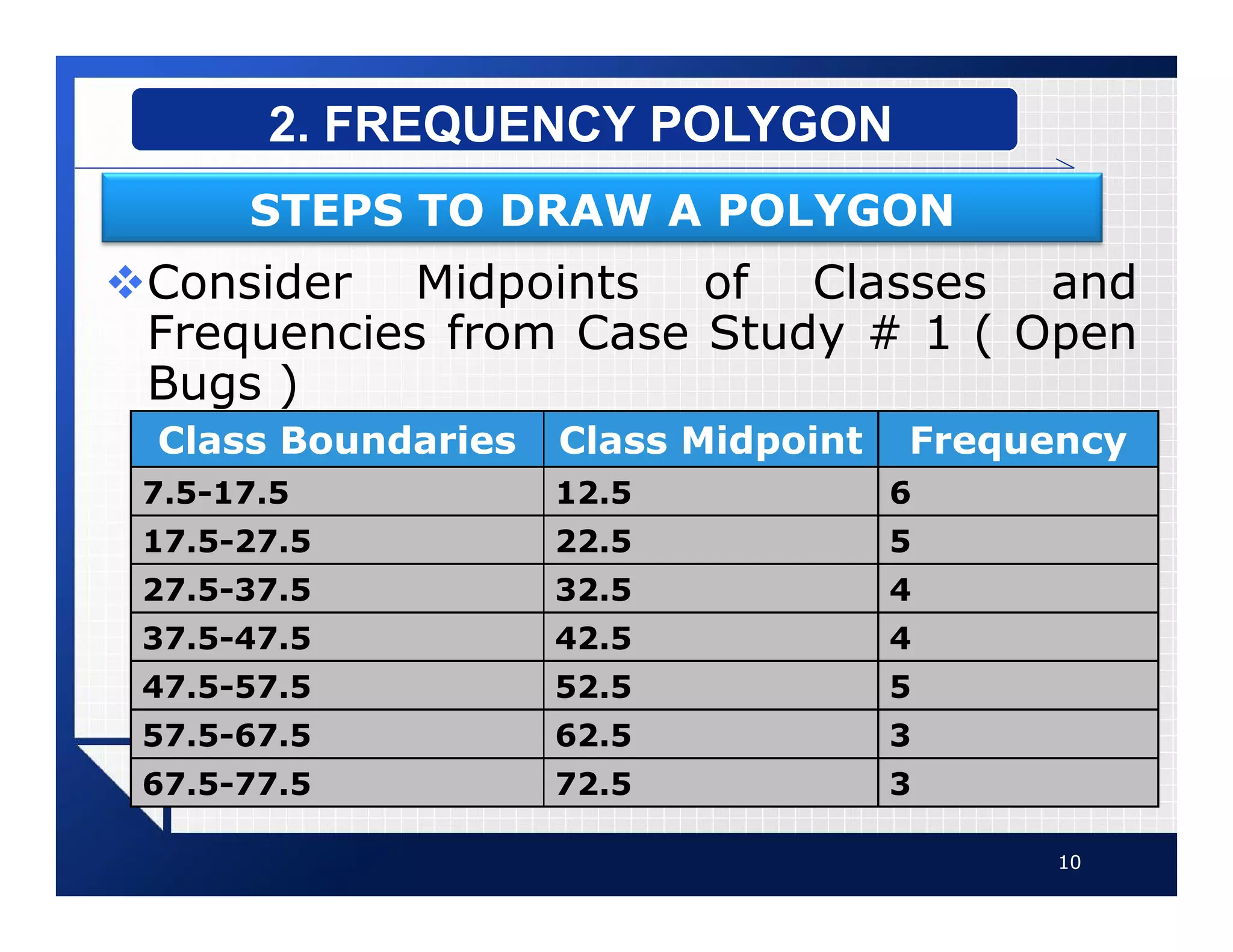
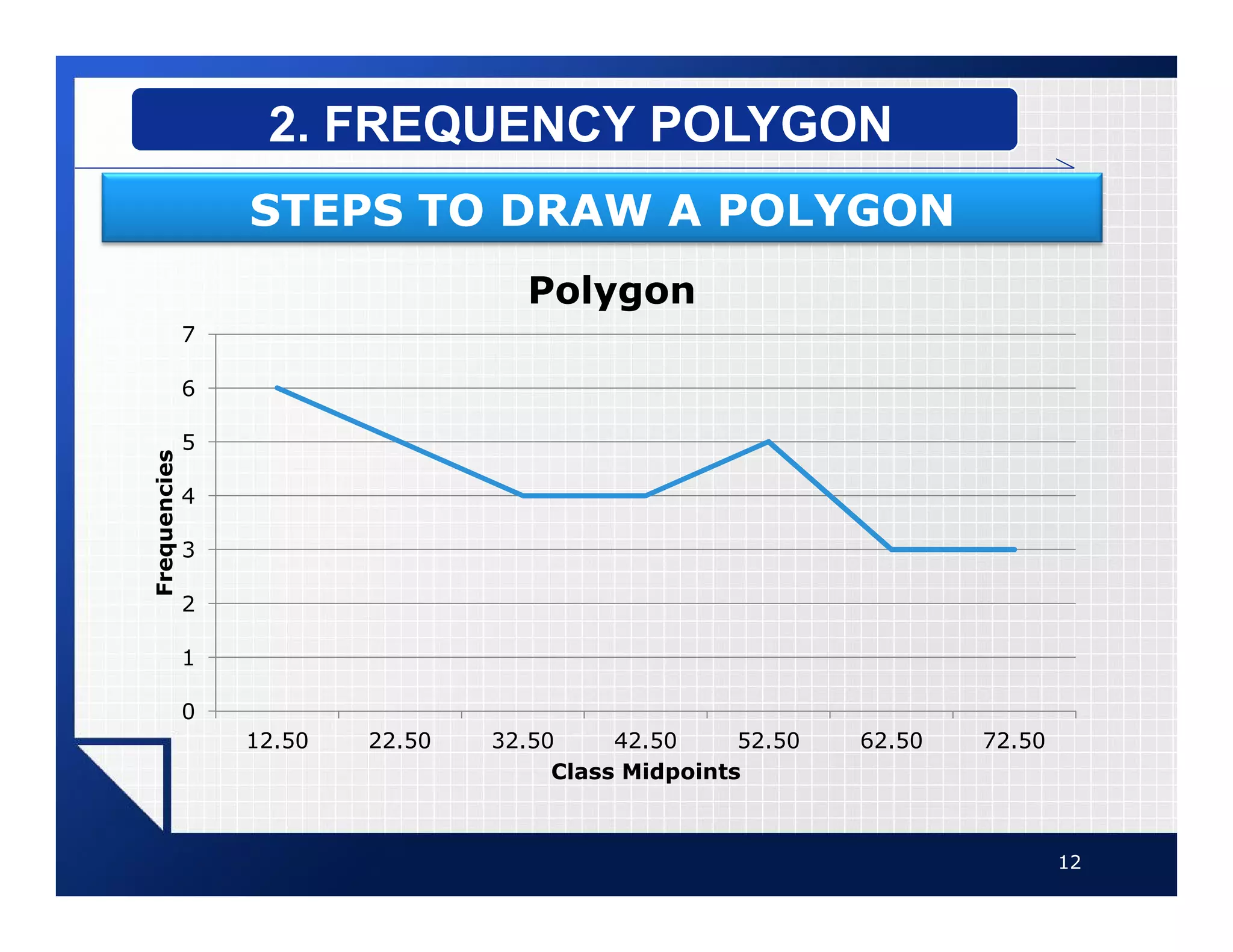
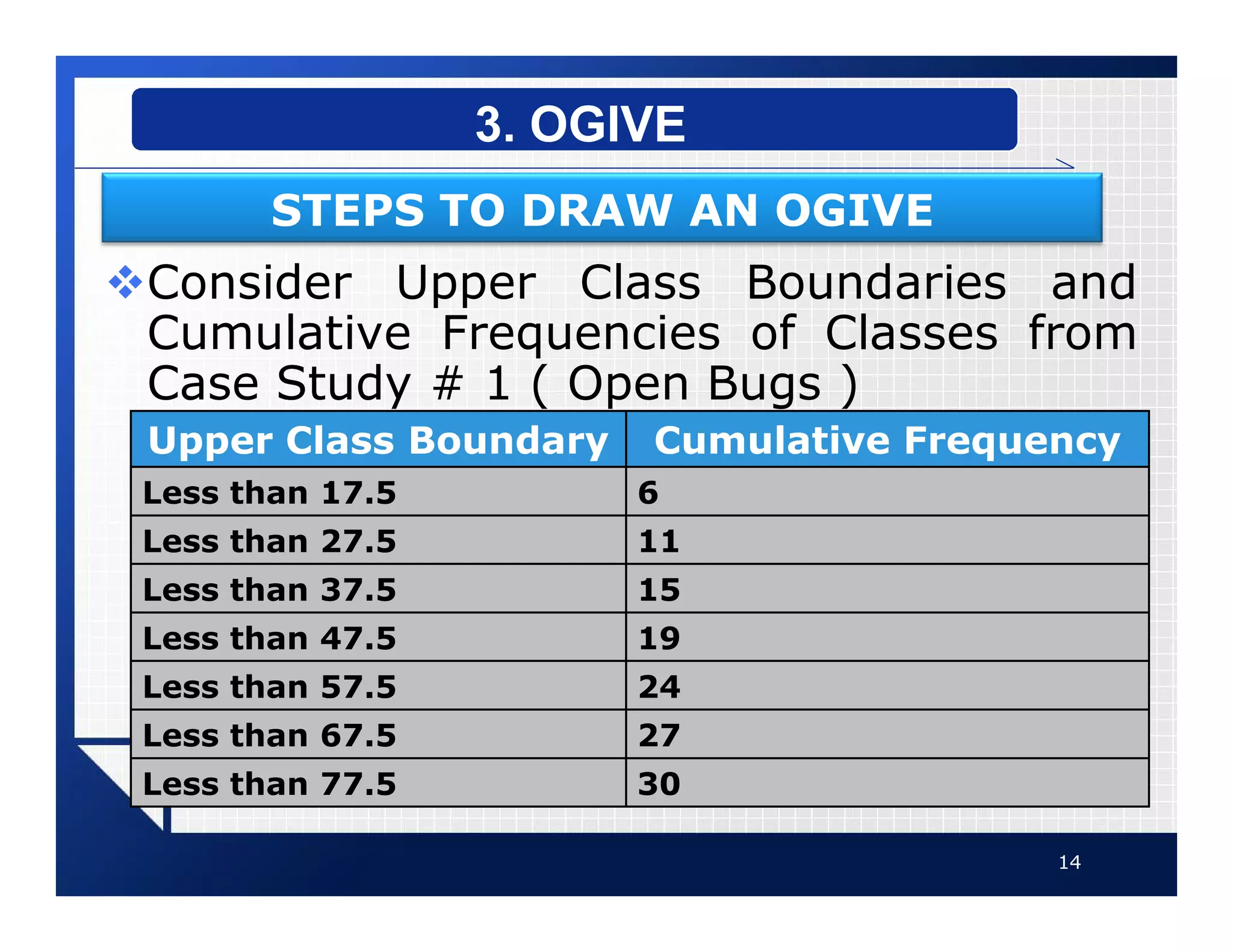
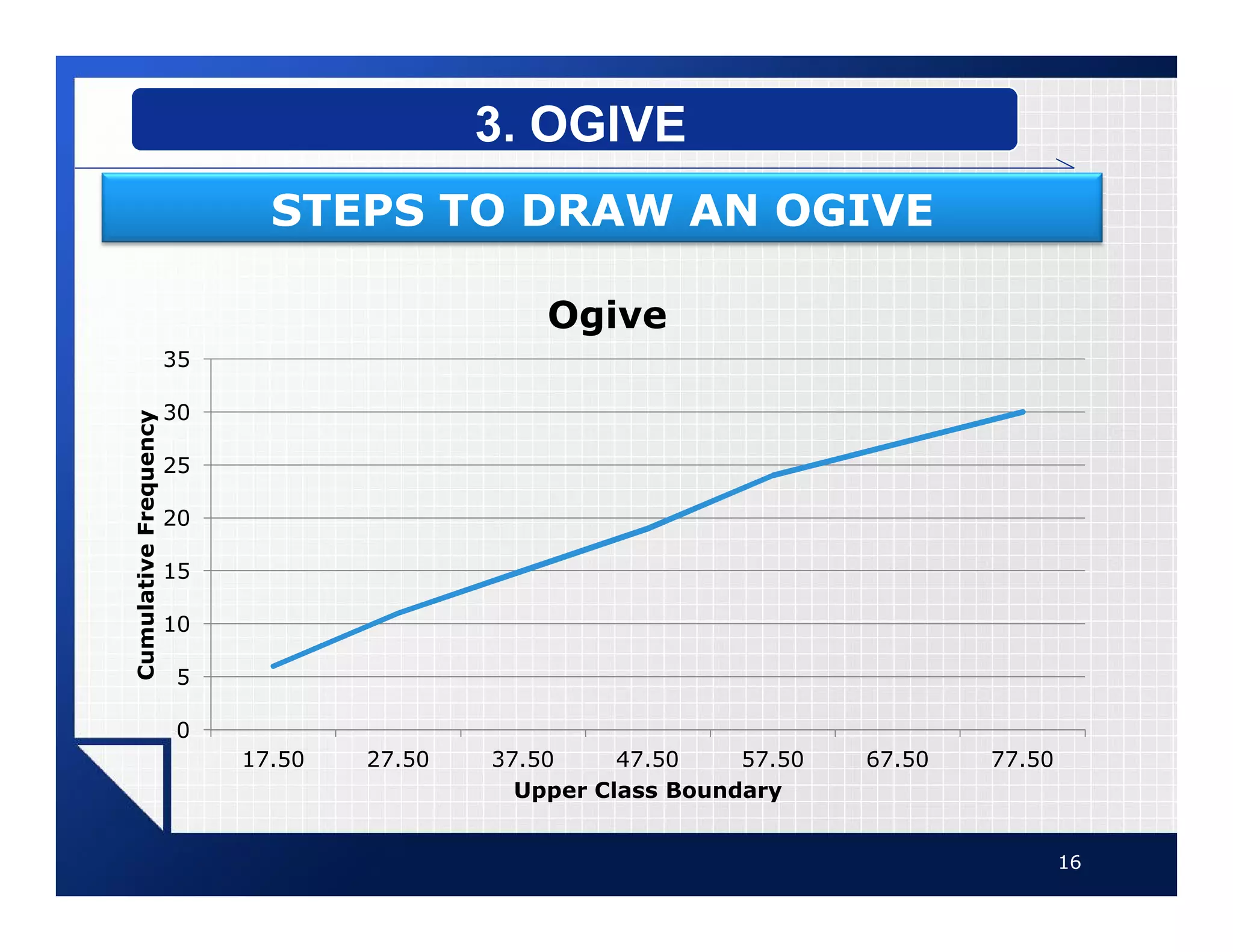
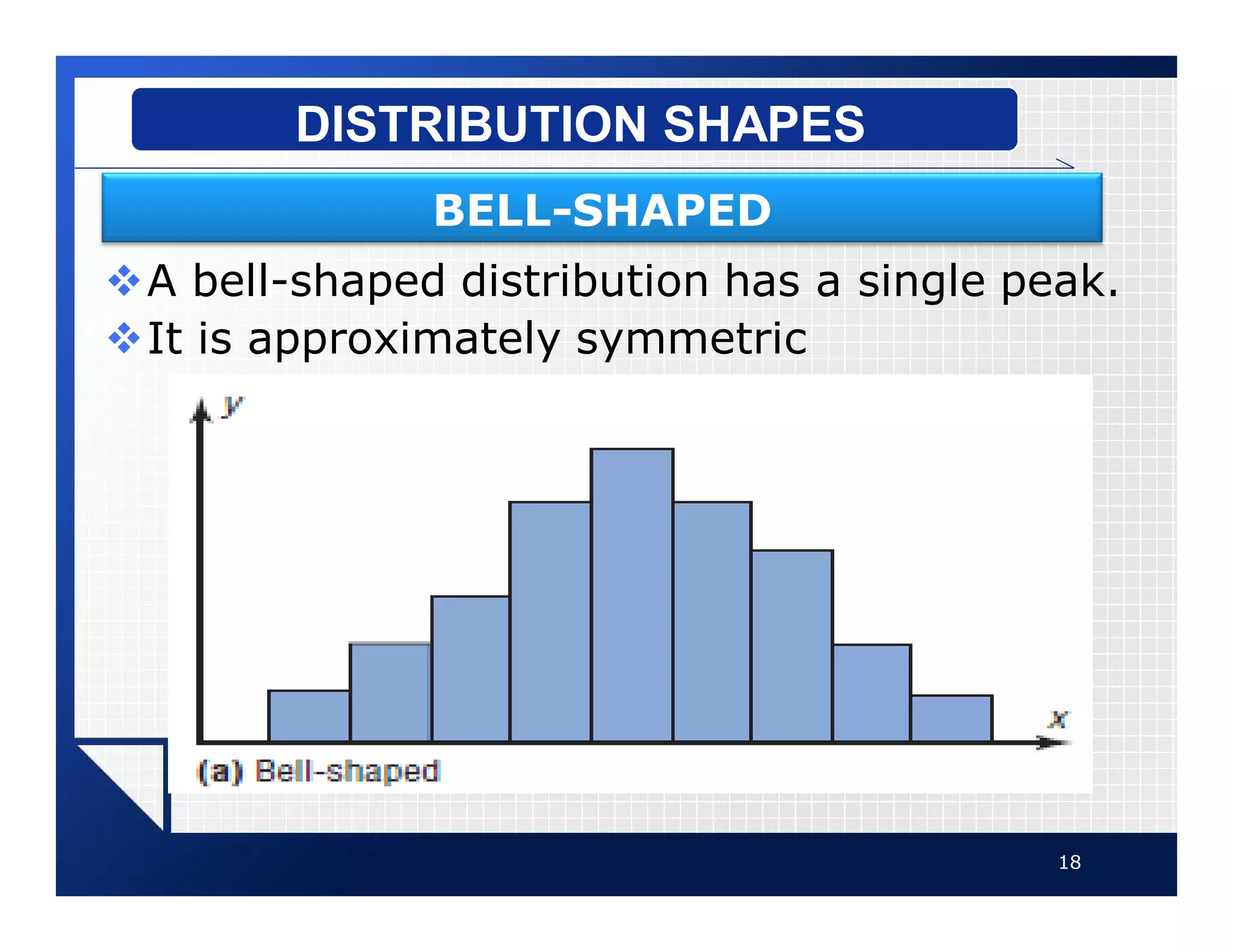
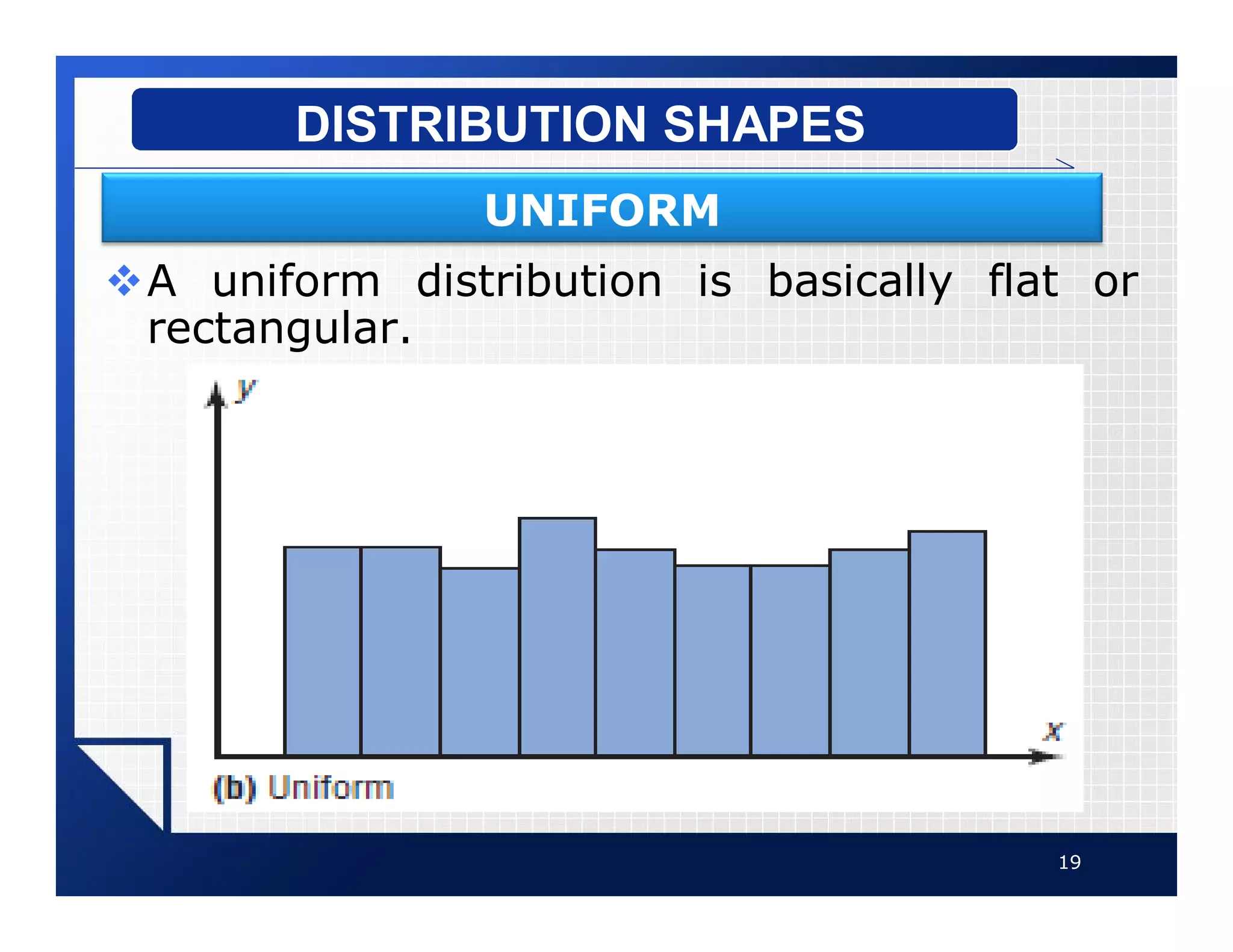
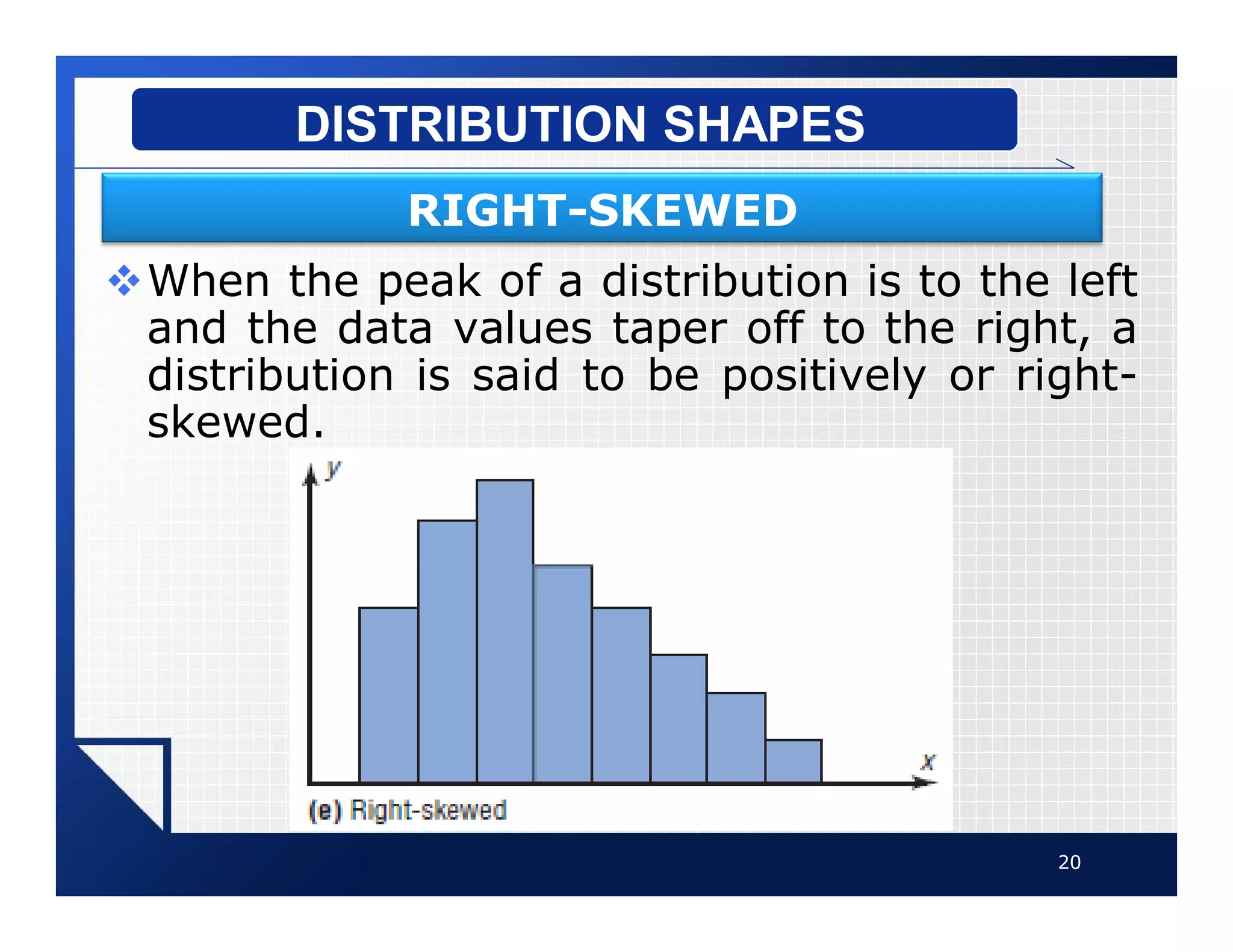
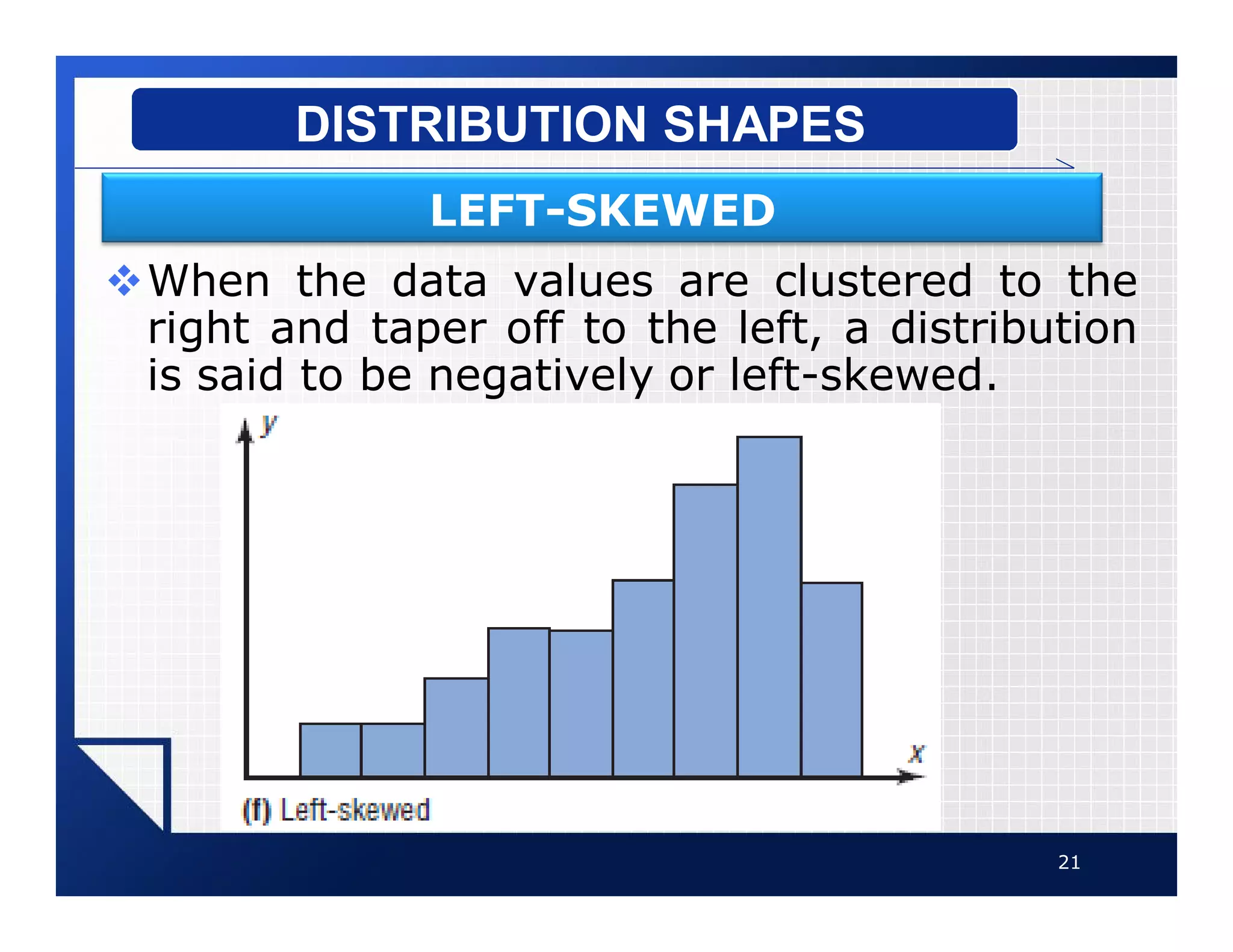
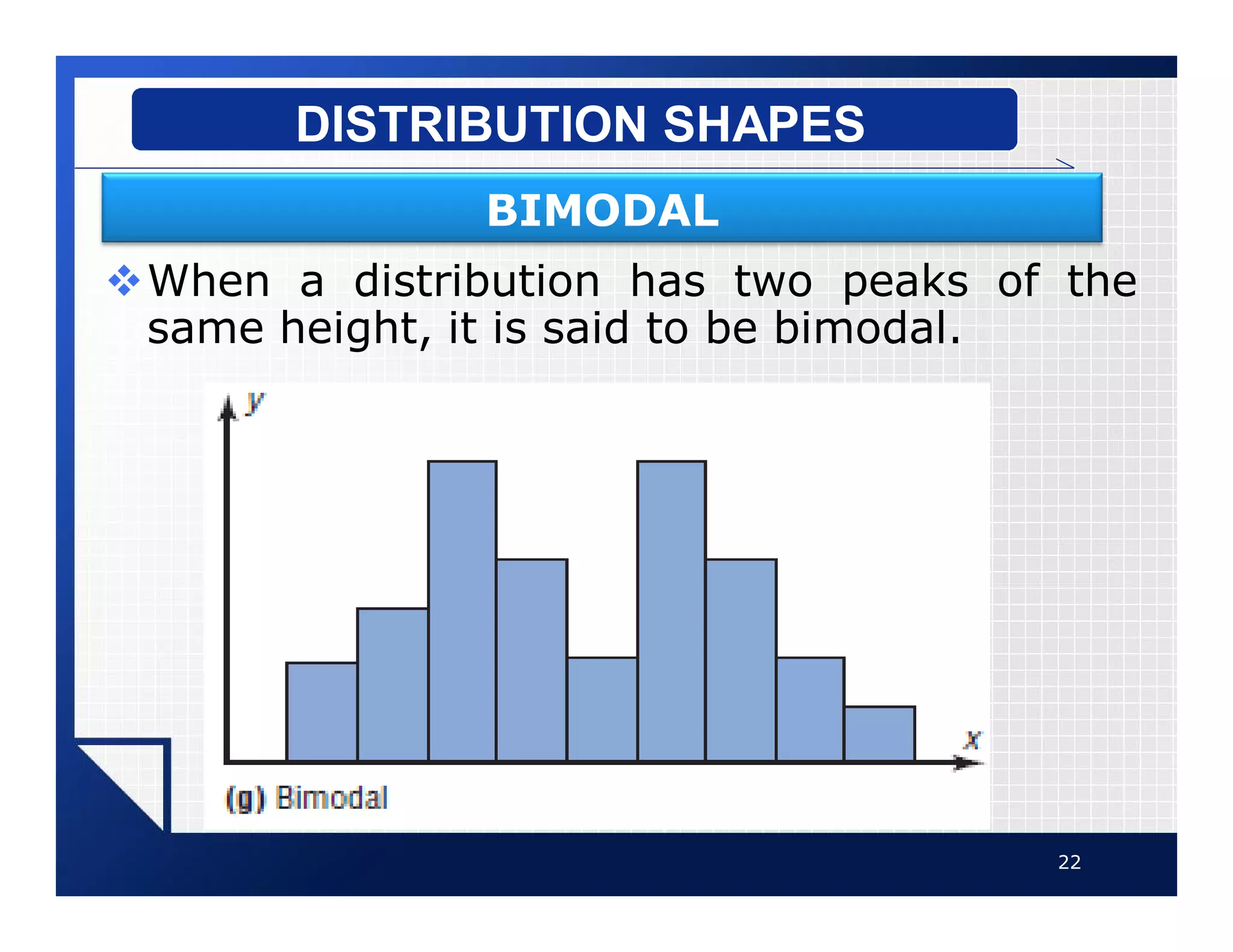
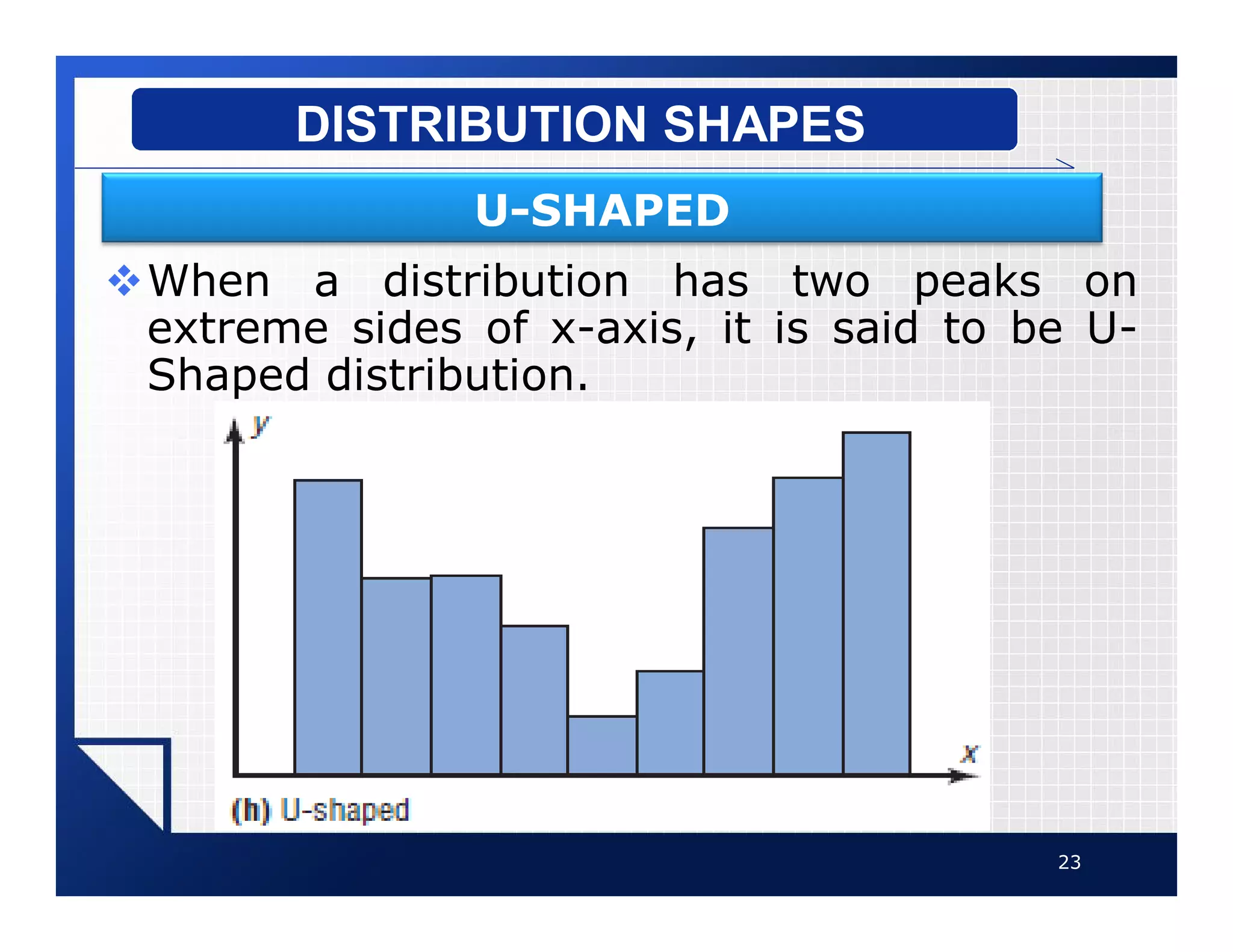
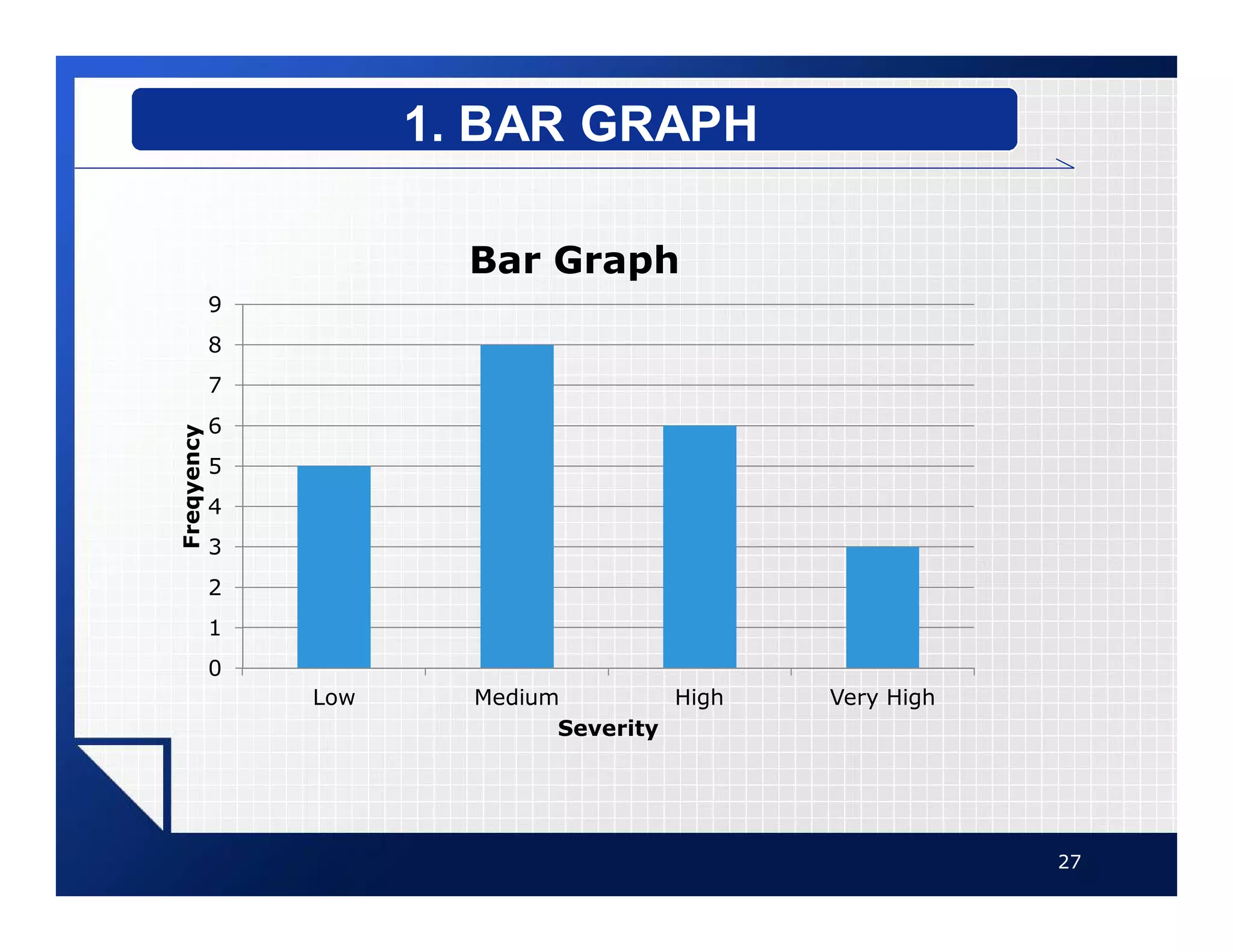
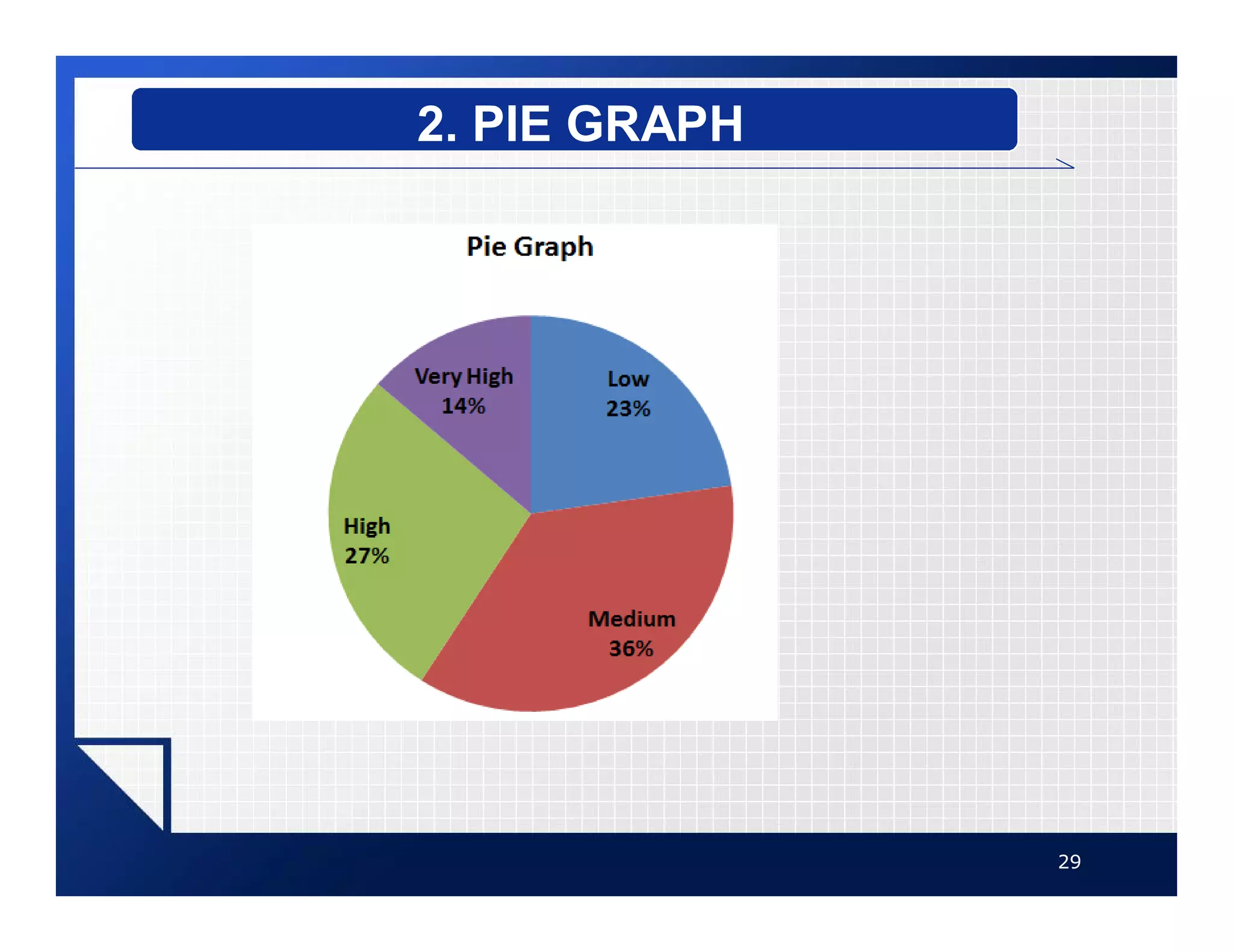
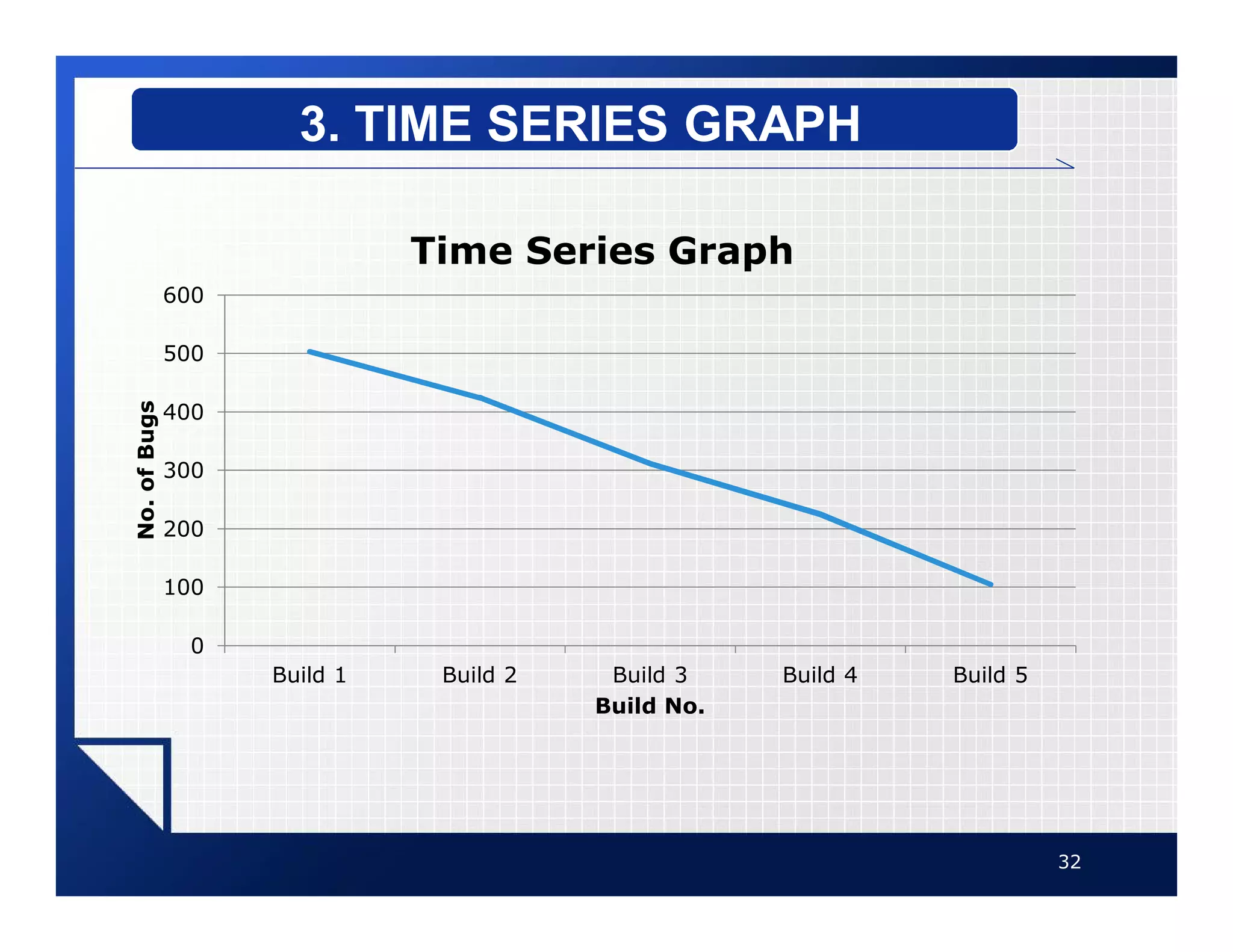
The document discusses different types of graphs that can be used to present data visually. It describes histograms, frequency polygons, cumulative frequency graphs (ogives), and how to construct each type of graph. Additional graph types covered include bar graphs, pie charts, and time series graphs. Common distribution shapes like bell-shaped, uniform, and skewed distributions are also outlined. The document provides examples and step-by-step instructions for drawing each graph using sample data sets.

1. Presentation of Data
1

2. 2
GRAPHS
1

3. vGraphs are used to present the
data in pictorial form.
vIt is easier for most people to
comprehend the meaning of
data presented graphically than
data presented numerically in
tables or frequency distributions.
vGraphs are used to discuss an
issue, reinforce a critical point,
or summarize a data set.
3
GRAPHS

4. vGraphs can also be used to
discover a trend or pattern in a
situation over a period of time.
vFollowing three are most
common types of graphs:
§ 1. Histogram
§ 2. Frequency Polygon
§ 3. Cumulative Frequency Graphs
(Ogive)
4
GRAPHS

5. vThe histogram is a graph that
displays the data by using
contiguous vertical bars of
various heights to represent the
frequencies of the classes.
5
1. HISTOGRAM

6. v Consider Class Boundaries and
Frequencies from Case Study # 1 ( Open
Bugs )
6
1. HISTOGRAM
STEPS TO DRAW A HISTOGRAM
Class Boundaries Frequency
7.5-17.5 6
17.5-27.5 5
27.5-37.5 4
37.5-47.5 4
47.5-57.5 5
57.5-67.5 3
67.5-77.5 3

7. vStep 1: Draw and label the x and y
axes.
vStep 2: Represent the frequency on
the y axis and the class boundaries
on the x axis.
vStep 3: Using the frequencies as
the heights, draw vertical bars for
each class.
7
1. HISTOGRAM
STEPS TO DRAW A HISTOGRAM

8. 8
1. HISTOGRAM
STEPS TO DRAW A HISTOGRAM
0
1
2
3
4
5
6
7
17.50 27.50 37.50 47.50 57.50 67.50 77.50
Frequency
Upper Class Boundary
Histogram

9. vThe frequency polygon is a
graph that displays the data by
using lines that connect points
plotted for the frequencies at the
midpoints of the classes.
vThe frequencies are represented
by the heights of the points.
9
2. FREQUENCY POLYGON

10. vConsider Midpoints of Classes and
Frequencies from Case Study # 1 ( Open
Bugs )
10
2. FREQUENCY POLYGON
STEPS TO DRAW A POLYGON
Class Boundaries Class Midpoint Frequency
7.5-17.5 12.5 6
17.5-27.5 22.5 5
27.5-37.5 32.5 4
37.5-47.5 42.5 4
47.5-57.5 52.5 5
57.5-67.5 62.5 3
67.5-77.5 72.5 3

11. vStep 1: Draw and label the x and y
axes.
vStep 2: Using the midpoints for the
x values and the frequencies as the
y values, plot the points.
vStep 3: Connect adjacent points
with line segments.
11
2. FREQUENCY POLYGON
STEPS TO DRAW A POLYGON

12. 12
2. FREQUENCY POLYGON
STEPS TO DRAW A POLYGON
0
1
2
3
4
5
6
7
12.50 22.50 32.50 42.50 52.50 62.50 72.50
Frequencies
Class Midpoints
Polygon

13. vThe ogive is a graph that
represents the cumulative
frequencies for the classes in a
frequency distribution.
vThe ogive or Cumulative
frequency graphs are used to
visually represent how many
values are below a certain upper
class boundary.
13
3. OGIVE

14. vConsider Upper Class Boundaries and
Cumulative Frequencies of Classes from
Case Study # 1 ( Open Bugs )
14
3. OGIVE
STEPS TO DRAW AN OGIVE
Upper Class Boundary Cumulative Frequency
Less than 17.5 6
Less than 27.5 11
Less than 37.5 15
Less than 47.5 19
Less than 57.5 24
Less than 67.5 27
Less than 77.5 30

15. vStep 1: Draw the x and y axes. Label
the x axis with the upper class
boundaries, and y axis with cumulative
frequencies.
vStep 2: Using the Upper Class
Boundaries for the x values and
Cumulative Frequencies as the y
values, plot the points.
vStep 3: Connect adjacent points
with line segments.
15
3. OGIVE
STEPS TO DRAW AN OGIVE

16. 16
3. OGIVE
STEPS TO DRAW AN OGIVE
0
5
10
15
20
25
30
35
17.50 27.50 37.50 47.50 57.50 67.50 77.50
Cumulative
Frequency
Upper Class Boundary
Ogive

17. vHistogram or Polygon are used
to analyze a distribution.
vFollowing are some common
distribution shapes:
§ Bell-Shaped
§ Uniform
§ Right-Skewed
§ Left-Skewed
§ Bimodal
§ U-shaped
17
DISTRIBUTION SHAPES

18. vA bell-shaped distribution has a single peak.
vIt is approximately symmetric
18
DISTRIBUTION SHAPES
BELL-SHAPED

19. vA uniform distribution is basically flat or
rectangular.
19
DISTRIBUTION SHAPES
UNIFORM

20. vWhen the peak of a distribution is to the left
and the data values taper off to the right, a
distribution is said to be positively or right-
skewed.
20
DISTRIBUTION SHAPES
RIGHT-SKEWED

21. vWhen the data values are clustered to the
right and taper off to the left, a distribution
is said to be negatively or left-skewed.
21
DISTRIBUTION SHAPES
LEFT-SKEWED

22. vWhen a distribution has two peaks of the
same height, it is said to be bimodal.
22
DISTRIBUTION SHAPES
BIMODAL

23. vWhen a distribution has two peaks on
extreme sides of x-axis, it is said to be U-
Shaped distribution.
23
DISTRIBUTION SHAPES
U-SHAPED

24. vSome other famous types of
graphs are as follows:
§ Bar Graph
§ Pie Graph
§ Time Series Graph
24
OTHER TYPES OF GRAPHS

25. vA bar graph represents the data
by using vertical or horizontal
bars whose heights or lengths
represent the frequencies of the
data.
25
1. BAR GRAPH

26. vConsider Severities and Frequencies from
Case Study # 2 ( Severity of Issues )
26
1. BAR GRAPH
Severity Frequency
Low 5
Medium 8
High 6
Very High 3

27. 27
1. BAR GRAPH
0
1
2
3
4
5
6
7
8
9
Low Medium High Very High
Freqyency
Severity
Bar Graph

28. vA pie graph is a circle that is
divided into sections according
to the percentage of frequencies
in each category of the
distribution.
28
2. PIE GRAPH

29. 29
2. PIE GRAPH

30. vA time series graph represents
data that occur over a specific
period of time.
30
3. TIME SERIES GRAPH

31. v In five different builds of ‘Message
Portal’, the number of bugs identified by
Quality Control Department are enlisted
below:
31
3. TIME SERIES GRAPH
Build No. No. of Bugs
Build 1 503
Build 2 424
Build 3 311
Build 4 225
Build 5 105

32. 32
3. TIME SERIES GRAPH
0
100
200
300
400
500
600
Build 1 Build 2 Build 3 Build 4 Build 5
No.
of
Bugs
Build No.
Time Series Graph