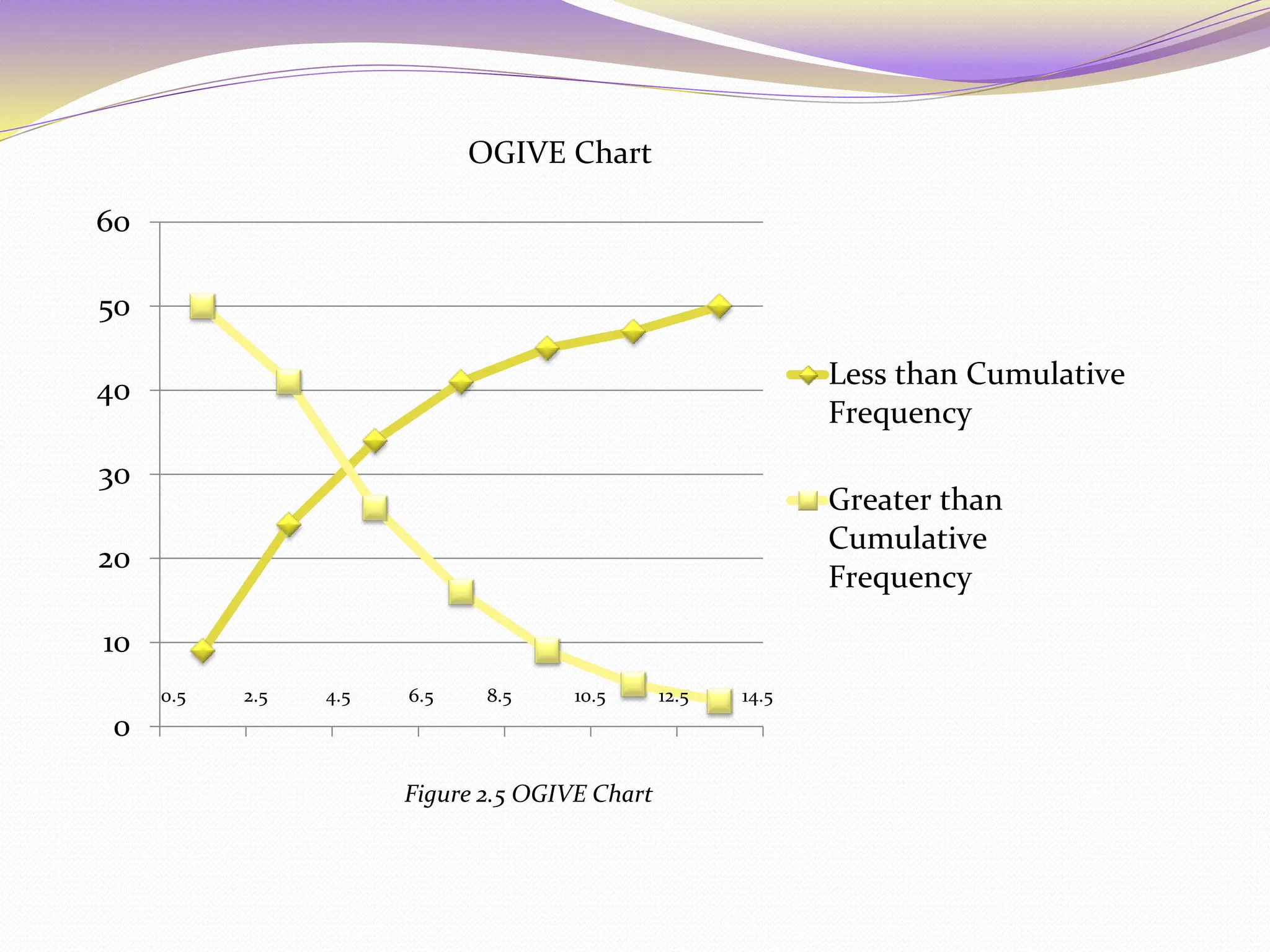
The document discusses frequency distribution in statistics, differentiating between ungrouped and grouped data, and outlines methods for creating frequency distribution tables and graphs. It describes five types of graphs: bar graphs, histograms, frequency polygons, pie charts, and ogive charts, including their construction and application. Additionally, it provides an example of a frequency distribution for family sizes among 50 families.

2. INTRODUCTION
In Statistics, we’ve studied about the Frequency
Distribution based on the given data. These data were
classified as grouped and ungrouped. Based on the data
given, we can determine how the table should be. For
making a Frequency Distribution Table for ungrouped
data is way too easy, while for grouped data, is quite
complicated.
The Frequency Distribution table is not only the
way to express or to file the data. We also use graphs to not
just illustrate the data given but also to be able us to
understand the data through in visual way. There are 5
different graphs: Bar Graph, Histogram, Frequency
Polygon, Pie Chart and the OGIVE Chart.

3. TABLE OF
CONTENTS
Title…………………………….…….Slide1
Introduction……………............…..Slide2
Table of Contents...………………..Slide3
Frequency Distribution…………...Slide 4
Bar Graph……………………….…..Slide 5-6
Histogram…………………………...Slide 7-8
Frequency Polygon…………….….Slide 9-10
Pie Chart…………………………….Slide 11-12
OGIVE Chart………………………..Slide 13-14
Generalization……………………...Slide 15
Credits……………………………….Slide 16

4. Is a table w/ the data arranged into different classes and number
of cases which fall into each class.
This table shows the Frequency Distribution for grouped data:
Frequency Distribution of the Number of Members of Each Family
Among 50 Families
No. of Members Tally Frequency (f) Class
Mark
Upper
Boundary
Lower
Boundary
1-2 IIIII-IIIII 9 1.5 2.5 0.5
3-4 IIIII-IIIII-IIIII 15 3.5 4.5 2.5
5-6 IIIII-IIIII 10 5.5 6.5 4.5
7-8 IIIII-II 7 7.5 8.5 6.5
9-10 IIII 4 9.5 10.5 8.5
11-12 II 2 11.5 12.5 10.5
13-14 III 3 13.5 14.5 12.5
N = 50 59.5 45.5

5. Is used to show relative sizes of data. Bars drawn proportional to the
data may be horizontal or vertical.
In constructing Bar Graphs, the following pointers are suggested:
1) Write the appropriate title for the graph indicating important important information.
2) Label both axes. For double or multiple bar graphs, use legend to identify bars.
The zero point should be clearly indicated.
3) Bars must be proportional to the quantities they are representing. The width of the
bars must be equal.
4) There must be uniform space between bars.
5) If necessary, highlight sources and footnotes.

6. 0
2
4
6
8
10
12
14
16
1 to 2 3 to 4 5 to 6 7 to 8 9 to 10 11 to 12 13 to 14
Bar Graph of Frequency Distribution of the No. of
Members of each Family Among 50 Families
Frequency Distribution
of the No. of Members of
each Family Among 50
Students
Figure 2.1 Bar Graph

7. It is a graph that is like the bar graph but
only differ in the bars which is joined together and
instead of using class intervals it uses the class
boundaries (LB – UB).
It consists of adjacent rectangles whose
width is the distance from the lower to the upper
class boundary and the height is the corresponding
frequency.

8. 0
2
4
6
8
10
12
14
16
Histogram of the Frequency Distribution of the
No. of Members of Each Family Among 50
Families
0.5 2.5 4.5 6.5 8.5 10.5 12.5 14.5
Figure 2.2 Histogram

9. It shows the relationship between two or more sets of
continuous data. For instance, it may show the relationship
between a population and time, or liquid capacity and distance.
In Constructing Frequency Polygon, the following Pointers are suggested:
1) State clearly the title of the graph indicating important information about the data.
2) Label both axes. For multiple Frequency polygon, a legend will facilitate understanding
of the information the graph wants to convey. The zero point should be clearly
indicated.
3) Connect plotted points from left to right.
4) Sources and footnotes should be provided, if necessary.
5) For multiple Frequency Polygons, one line should be distinguished from the other. This
can be done through the use of color or line forms.

10. 0
2
4
6
8
10
12
14
16
1 to 2 3 to 4 5 to 6 7 to 8 9 to 10 11 to 12 13 to 14
Frequency Polygon of Frequency Distribution of the
No. of Members of each Family Among 50 Families
Frequency Polygon of
Frequency
Distribution of the
No. of Members of
each Family Among
50 Families
Figure 2.3 Frequency Polygon

11. Is best used to compare parts to a whole.
The size of each sector of the circle is proportional
to the size of the category that it represents
To make a Circle Graph, the following pointers are suggested:
1) Organize the data on the table by providing column to the fractional parts
or percent each quantity is of the whole and the number of degrees
representing each fractional part.
2) On a circle, construct successive central angles using the number of
degrees representing each part.
3) Label each part with the appropriate title for the graph.

12. 18%
30%
20%
14%
8%
6% 4%
Pie Chart of the Frequency Distribution of the No. of
Members of each Family Among 50 Families
1 to 2
3 to 4
5 to 6
7 to 8
9 to 10
11 to 12
13 to 14
Figure 2.4 Pie Chart

13. Is a Frequency polygon where the cumulative frequency of
each class is plotted against the corresponding class boundary.
For the same data, the less than ogive and the greater than
ogive are graphed in one grid. Take note of the importance of the
intersection of the ogives.

14. 0
10
20
30
40
50
60
Less than Cumulative
Frequency
Greater than
Cumulative
Frequency
0.5 2.5 4.5 6.5 8.5 10.5 12.5 14.5
OGIVE Chart
Figure 2.5 OGIVE Chart

15. GENERALIZATIO
N
There are 4 Graphs to show the Frequency Distribution of
data. It is: Bar Graph, Histogram, Frequency Polygon and the
Pie Chart.
OGIVE Chart is used to illustrate the Less than cumulative
Frequency and the Greater than cumulative Frequency.

16. JOHN ROME R. ARANAS
Creator
SOURCES AND RESOURCES
Myself
New Century Mathematics by Phoenix
Publishing
Statistics: Rudiments and Analysis of Data
by ICS Publishing
Math Notebook
Ms. Charmaigne Marie Mahamis
Google
Wikipedia