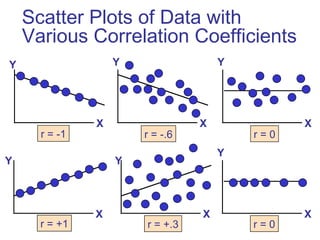
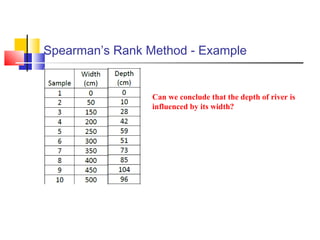
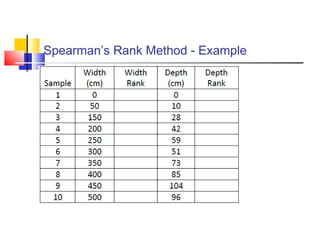
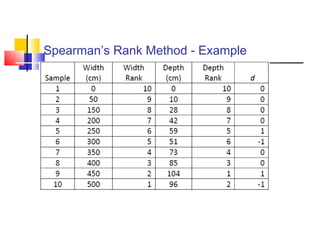
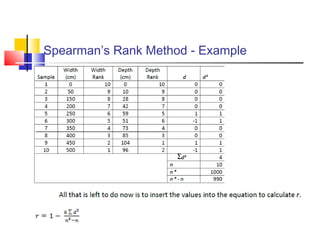
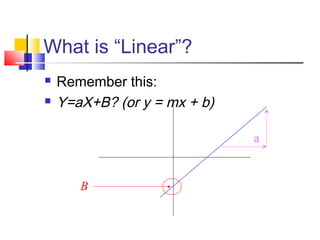
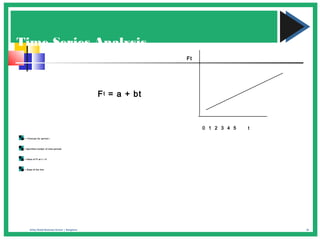
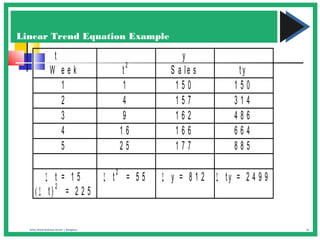
The document discusses various forecasting techniques including covariance, correlation coefficients, scatter plots, and linear regression. It defines covariance and correlation, and how they measure the strength and direction of relationships between variables. Linear regression finds the linear trend line that best fits the data using the method of least squares to calculate the slope (a) and y-intercept (b) values. Time series analysis can also use linear regression to model a linear trend over time and make forecasts by extending the trend line into the future.

1. Forecasting Techniques

2. Recall: Covariance
1
))((
),(cov 1
−
−−
=
∑=
n
YyXx
yx
n
i
ii

3. cov(X,Y) > 0 X and Y are positively correlated
cov(X,Y) < 0 X and Y are inversely correlated
cov(X,Y) = 0 X and Y are independent
Interpreting Covariance

4. Correlation coefficient
 Pearson’s Correlation Coefficient is standardized covariance (unitless):
yx
yxariance
r
varvar
),(cov
=

5. Correlation
 Measures the relative strength of the linear
relationship between two variables
 Unit-less
 Ranges between –1 and 1–1 and 1
 The closer to –1, the stronger the negative linear
relationship
 The closer to 1, the stronger the positive linear
relationship
 The closer to 0, the weaker any positive linear
relationship

6. Scatter Plots of Data with
Various Correlation Coefficients
Y
X
Y
X
Y
X
Y
X
Y
X
r = -1 r = -.6 r = 0
r = +.3r = +1
Y
X
r = 0

7. Calculating by hand…
1
)(
1
)(
1
))((
varvar
),(cov
ˆ
1
2
1
2
1
−
−
−
−
−
−−
==
∑∑
∑
==
=
n
yy
n
xx
n
yyxx
yx
yxariance
r
n
i
i
n
i
i
n
i
ii

8. Spearman’s Rank Method

9. Spearman’s Rank Method - Example
Can we conclude that the depth of river is
influenced by its width?

10. Spearman’s Rank Method - Example

11. Spearman’s Rank Method - Example

12. Spearman’s Rank Method - Example

13. Coefficient of Determination or R-
squared
 The percentage of variation in the
dependent variable can be attributed to
the variation in the independent
variable.
 It is simply the square of the correlation
coefficient!

14. Linear regression
In correlation, the two variables are treated as equals. In regression, one
variable is considered independent (=predictor) variable (X) and the other the
dependent (=outcome) variable Y.

15. What is “Linear”?
 Remember this:
 Y=aX+B? (or y = mx + b)
B
a

16. Finding ‘a’ & ‘b’ through the
method of LEASTLEAST
SQUARESSQUARES
So, you firs find out ‘a’ and then use the mean
values to get ‘b’.

17. Example

18. Example

19. Find the equation here!
Ad Spend Sales Revenue
2 60
5 100
4 90
6 90
3 80
Y = Dependent variable (in this case Sales)

20. 20Amity Global Business School | Bangalore
Time Series Analysis
Ft = Forecast for period t
t = Specified number of time periods
a = Value of Ft at t = 0
b = Slope of the line
Ft = a + bt
0 1 2 3 4 5 t
Ft

21. 21Amity Global Business School | Bangalore
Calculating a and b
b =
n (ty) - t y
n t
2
- ( t)
2
a =
y - b t
n
∑∑∑
∑∑
∑∑
Same as the Least Squares Method, just that in this case, t is the independent variable.

22. 22Amity Global Business School | Bangalore
Linear Trend Equation Example
t y
W e e k t
2
S a le s ty
1 1 1 5 0 1 5 0
2 4 1 5 7 3 1 4
3 9 1 6 2 4 8 6
4 1 6 1 6 6 6 6 4
5 2 5 1 7 7 8 8 5
Σ t = 1 5 Σ t
2
= 5 5 Σ y = 8 1 2 Σ ty = 2 4 9 9
( Σ t)
2
= 2 2 5

23. 23Amity Global Business School | Bangalore
Linear Trend Calculation
y = 143.5 + 6.3t
a =
812 - 6.3(15)
5
=
b =
5 (2499) - 15(812)
5(55) - 225
=
12495 - 12180
275 - 225
= 6.3
143.5

24. Thank you!Thank you!