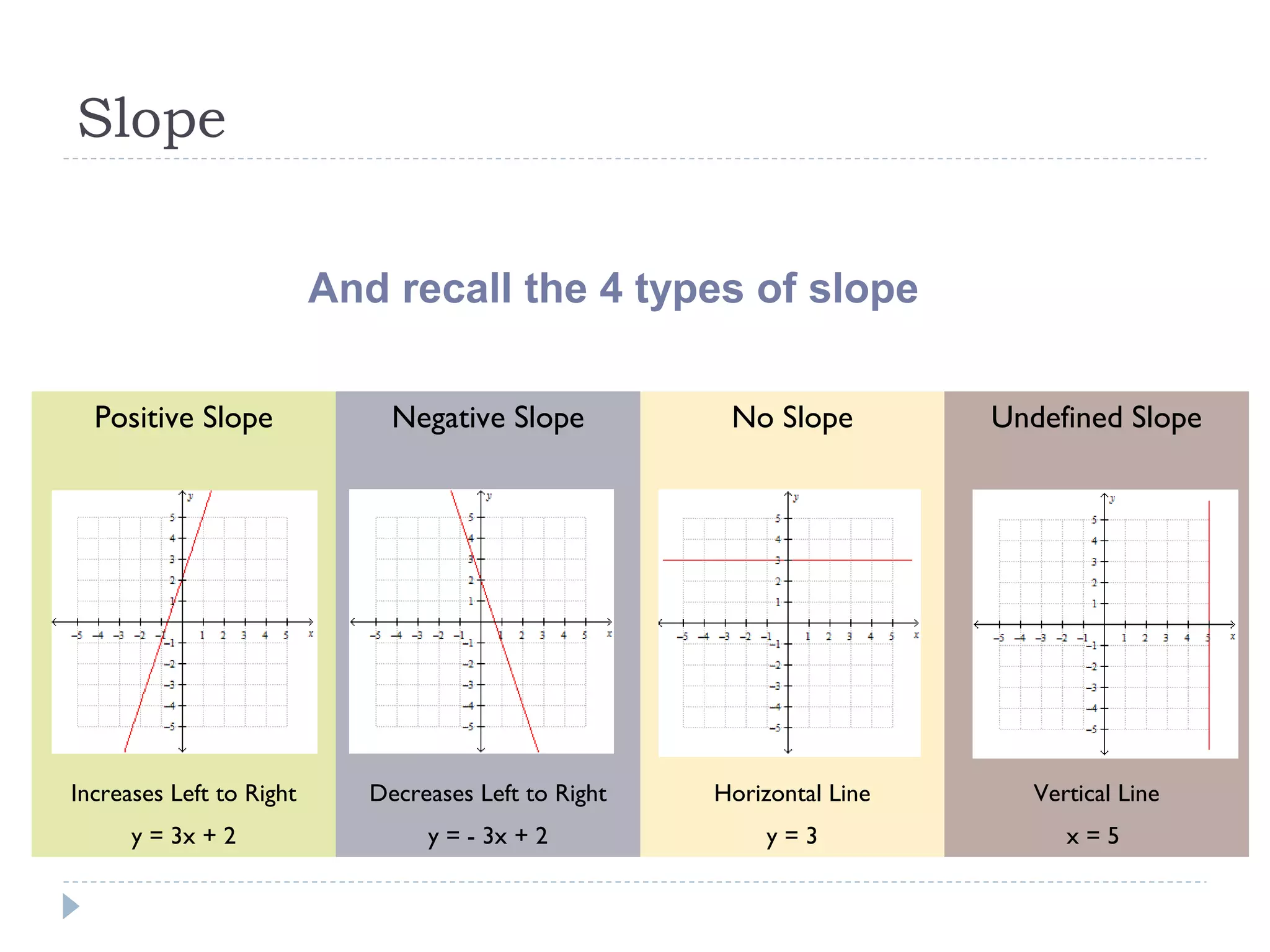
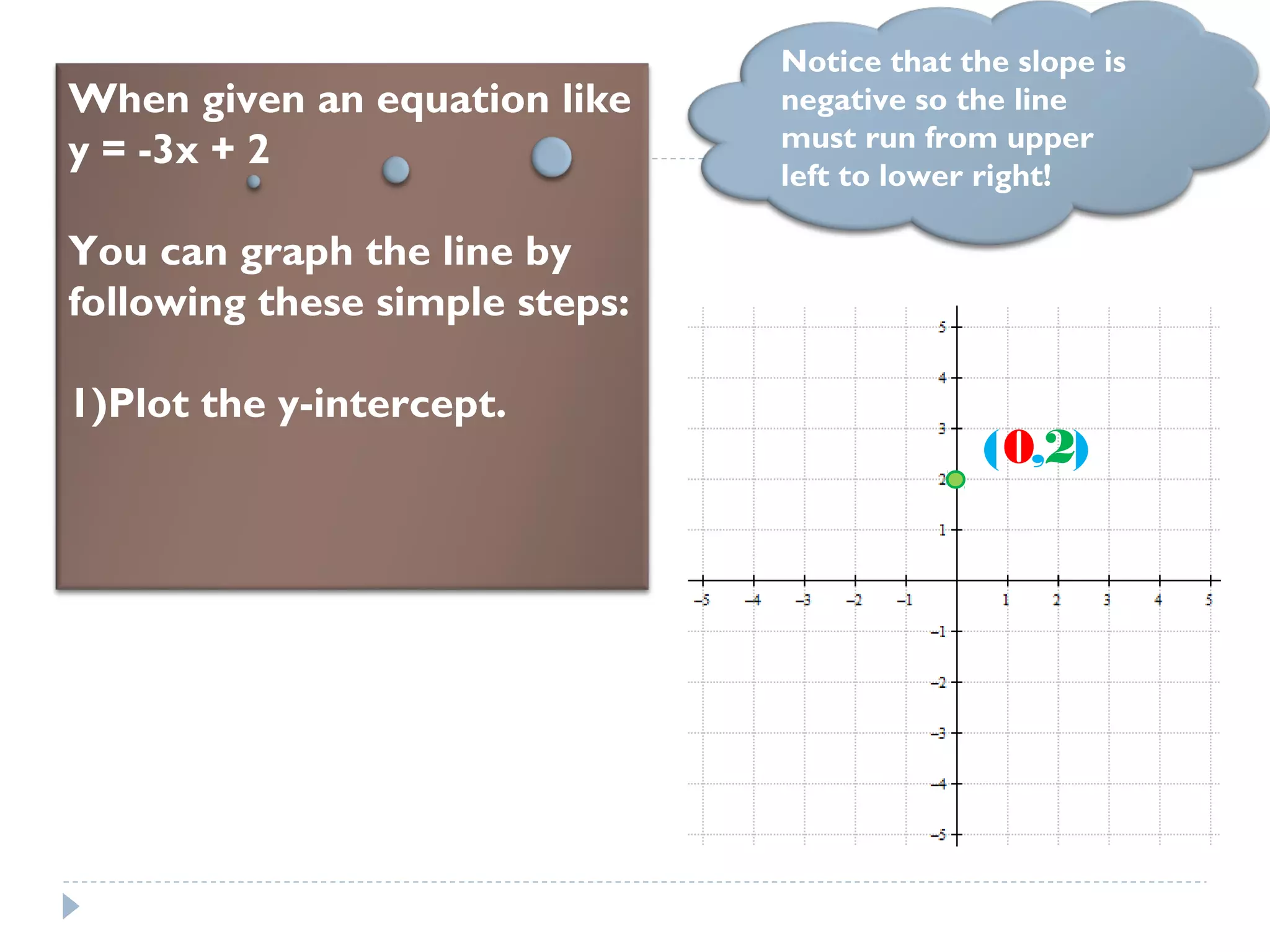
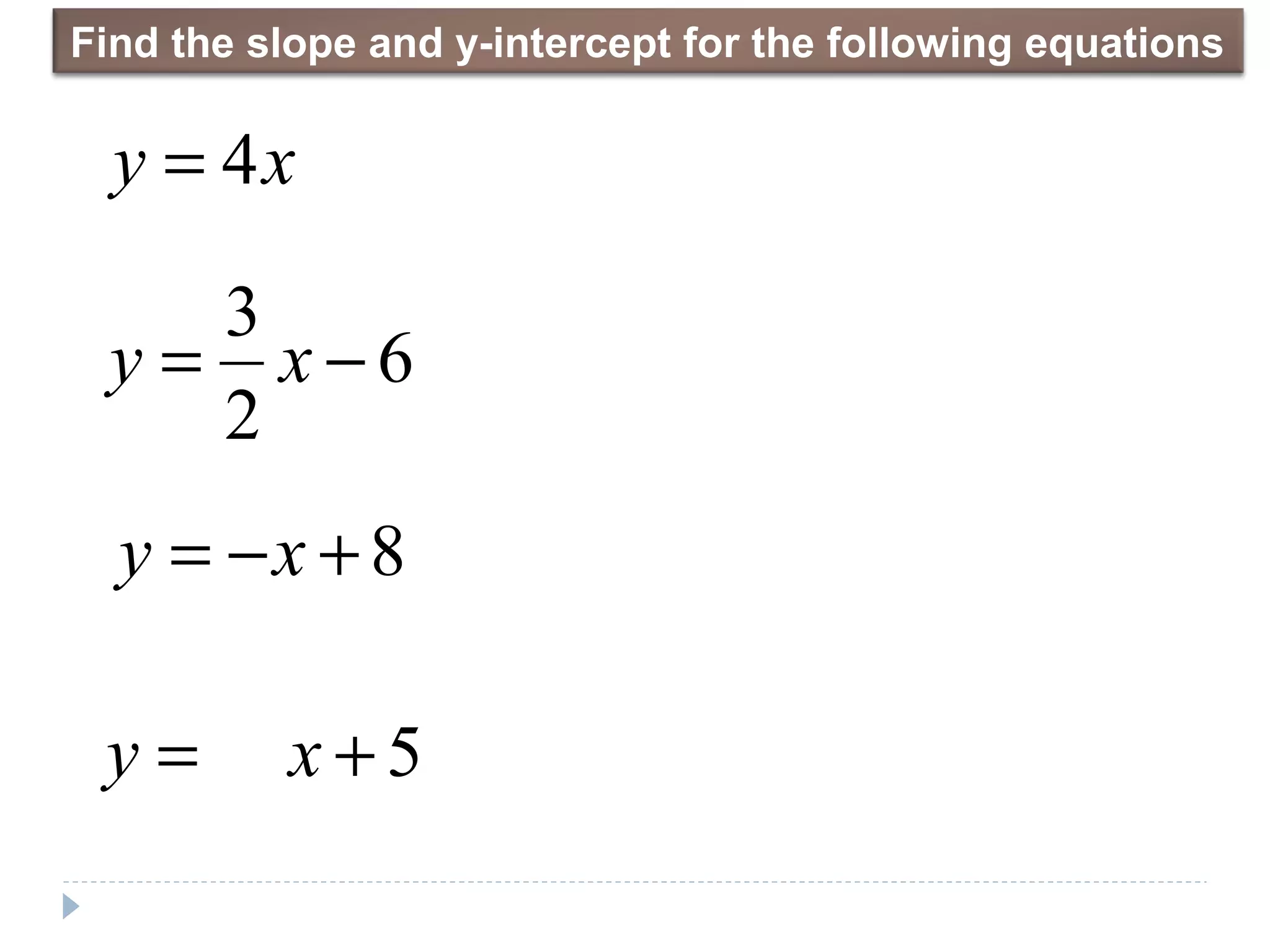Slope-intercept form is represented by the equation y=mx+b, where m is the slope and b is the y-intercept. There are three methods to find the slope: rise over run, change in y over change in x, and point-slope formula. The slope tells the rate of change, while the y-intercept is the initial value when x=0. To graph a line in slope-intercept form, you plot the y-intercept and then use the slope to trace successive points on the line by calculating the rise over run at each interval of x. Word problems can be modeled using this form by identifying the independent and dependent variables and finding their relationship through calculating slope from ordered pairs of known values.

1. Slope-Intercept Form
y=mx + b

2. Slope
Recall the three methods we can use to find slope.
bmxy
xx
yy
m
run
rise
m
+=
−
−
=
=
12
12

3. Slope
And recall the 4 types of slope
Positive Slope Negative Slope No Slope Undefined Slope
Increases Left to Right Decreases Left to Right Horizontal Line Vertical Line
y = 3x + 2 y = - 3x + 2 y = 3 x = 5

4. Slope
There are 3 methods we can
use to find slope!
Each one works best
for certain situations.
bmxy
xx
yy
m
run
rise
m
+=
−
−
=
=
12
12
Remember this guy?

5. This is Slope Intercept Form.
We can use this equation to
find the slope of a line and the
y-intercept.
bmxy +=
Remember this guy?

6. The slope is a constant but it
is always affected by something.
The slope tells you the rate of change over each interval or
time or an occurrence.
initial
…a yearevery
each …a month
per
…a day

7. The y-intercept is a constant.
This means that it is the starting point in a word problem, or a
value that does not change and is not affected by anything
happening within the word problem.
initial originalstarting
where x = 0 (flat) fee
one time cost of one item

8. You Try!

9. xy 4=
6
2
3
−= xy
8+−= xy
5+= xy
Find the slope and y-intercept for the following equations

10. xy 4=
6
2
3
−= xy
8+−= xy
5+= xy
0int,4 =−= ym
6int,
2
3
−=−= ym
8int,1 =−−= ym
5int,1 =−= ym
How did you do?

11. Graphing

12. When given an equation like
y = -3x + 2
You can graph the line by
following these simple steps:

13. When given an equation like
y = -3x + 2
You can graph the line by
following these simple steps:
1)Plot the y-intercept.
(0,2)

14. When given an equation like
y = -3x + 2
You can graph the line by
following these simple steps:
1)Plot the y-intercept.
Notice that the slope is
negative so the line
must run from upper
left to lower right!
(0,2)

15. (1,-1)
When given an equation like
y = -3x + 2
You can graph the line by
following these simple steps:
1)Plot the y-intercept.
2)Use the slope to trace
(rise / run) to the next point
on the line. -3 is
actually - 3
/1
Notice that the slope is
negative so the line
must run from upper
left to lower right!
(0,2)

16. When given an equation like
y = -3x + 2
You can graph the line by
following these simple steps:
1)Plot the y-intercept.
2)Use the slope to trace
(rise / run) to the next point
on the line. 3 is
actually 3
/1
3)Connect the points with a
line.
(1,-1)
(0,2)
Notice that the slope is
negative so the line
must run from upper
left to lower right!

17. Review Problems
Given: The slope of a line is -2 and the y-intercept is 3.
Write the equation of the line in slope-intercept form.
The information provided is enough for you to write the
equation. m = -2, b = 3 and slope-intercept form is
y = mx + b.
32 +−= xy

18. Write the equation of the line in slope-intercept form
that passes through the points: (2,-3) and (-12,-8).
To write an equation in slope-intercept form we need the
slope.
1.Use the ordered pairs to find the slope.
14
5
14
5
212
38
212
)3(8
=
−
−
=
−−
+−
=
−−
−−−
=m

20. Write the equation of the line in slope-intercept form
that passes through the point (9,-2) and is
a)Parallel to y = -4x+7
b)Perpendicular to y = -4x+7
Parallel Perpendicular
1. Slope of the parallel is -4
2. m = -4 and (9,-2)
1. Slope of the perpendicular is ¼ .
2. m = ¼ and (9,-2)
b
b
b
bmxy
=
+−=−
+−=−
+=
34
362
)9)(4(2
( )( ) ( ) ( )( )
b
b
b
b
b
b
bmxy
=−
=−
+=−
+





=−
+





=−
+





=−
+=
4
17
417
498
4
4
9
424
4
9
2
)9(
4
1
2
344 +−= xy
4
17
4
1
−= xy

21. Celia is out picking strawberries. She had 26 strawberries in her bucket
after she had been picking for 17 minutes. She is now finished after
spending 85 minutes picking. She has 138 strawberries.
Write an equation to model the number of strawberries, n, Celia picked per
minute, t.
1. Independent
and Dependent
Variables
2. After you
write the
ordered pairs,
find m.
3. Use the values to find the
equation.
(Let’s practice with point-slope
formula this time)
The number
picked depends
on the time
spent picking.
Number is
dependent on
time, so the
ordered pairs will
look like:
(t, n)
(17, 26) and
(85, 138)
17
28
68
112
8517
13826
=
−
−
=
−
−
=
m
m
m
( )
2
17
28
28
17
28
26
17
17
28
26
)1(1
−=
−=−
−=−
−=−
xy
xy
xy
xxmyy
So, what does this mean?
(let’s “interpret” a look on the next slide)

22. 2
17
28
−= xy
We determined that the number of
strawberries she had depended on the amount
of time she had been picking.
The slope, 28/17, is the change in “y” or
dependent value, which is n in this case over the
change in “x” or the independent value, which
is t in this case.
So we can say that
1. Independent
and Dependent
Variables
The number
picked depends
on the time
spent picking.
Number is
dependent on
time, so the
ordered pairs will
look like:
(t, n)
minutesinchange
esstrawberriof#inchange
17
28
=

23.  Interpret slope : for every 17 minutes she picked 28
strawberries.
 Or, if we find the unit rate by dividing, we get 1.647,
which means for every 1 minute she picked about
1.647 strawberries.
 Interpret y-intercept : she began with -2
strawberries. This is not realistic!