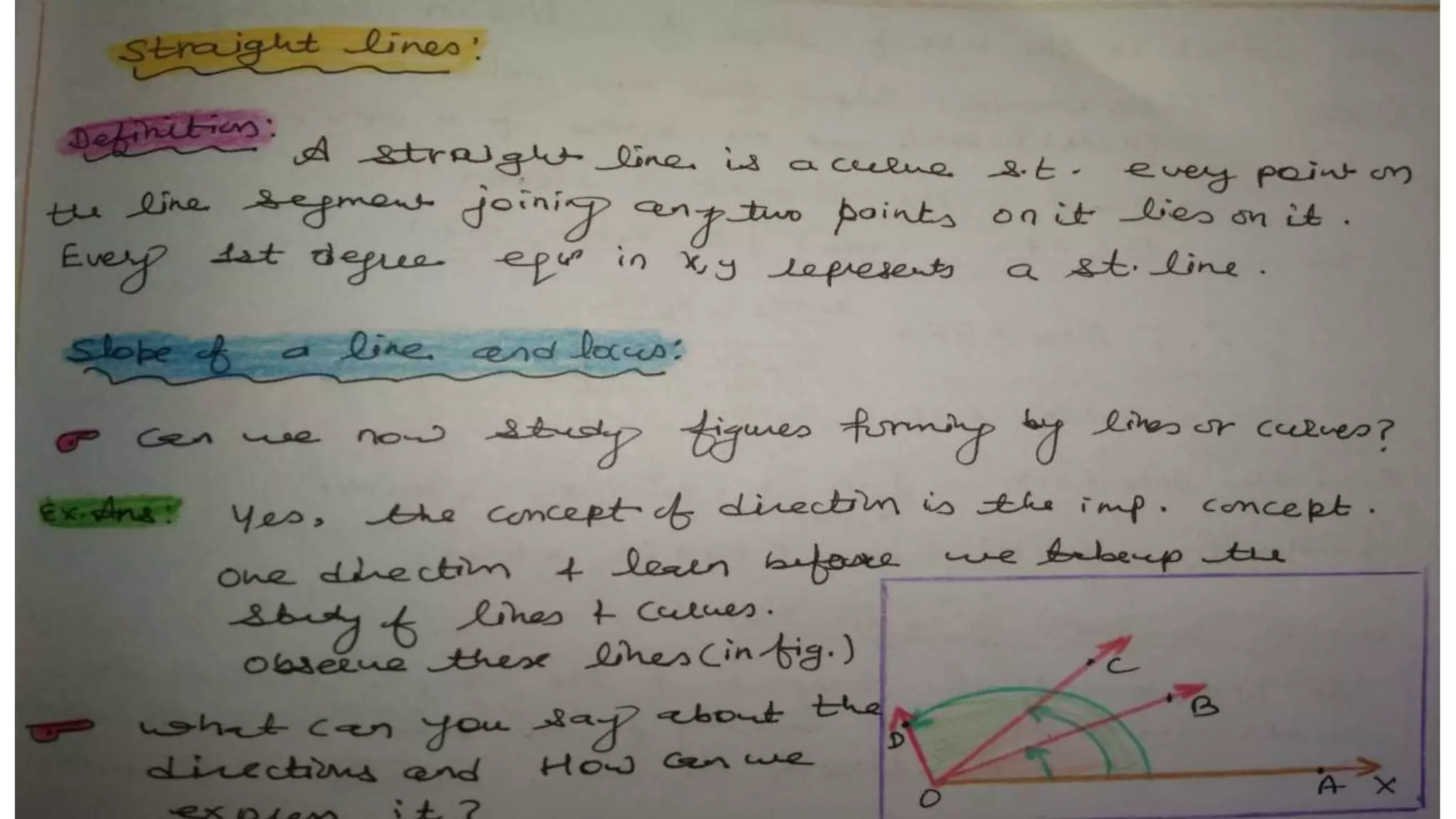
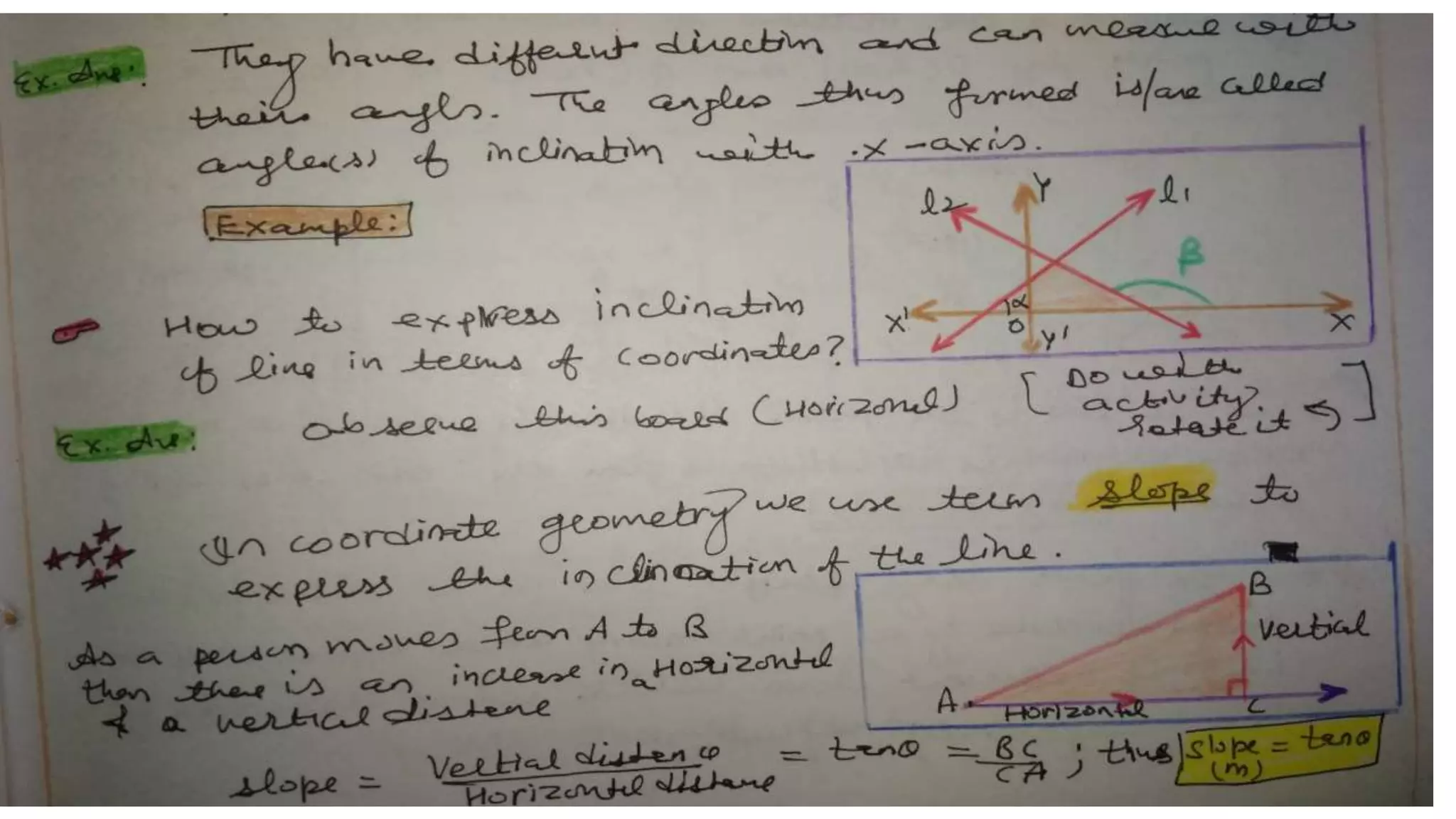
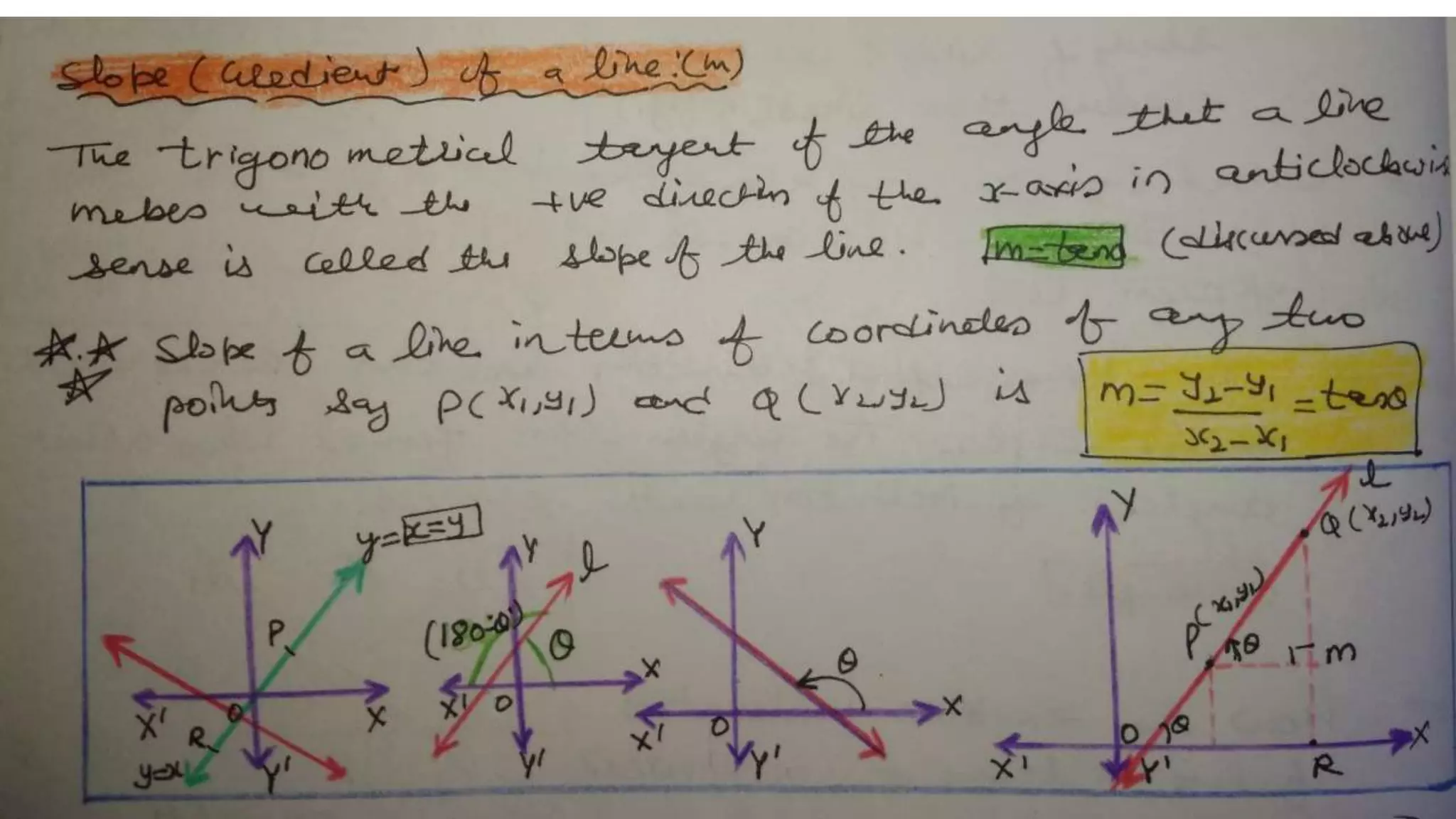
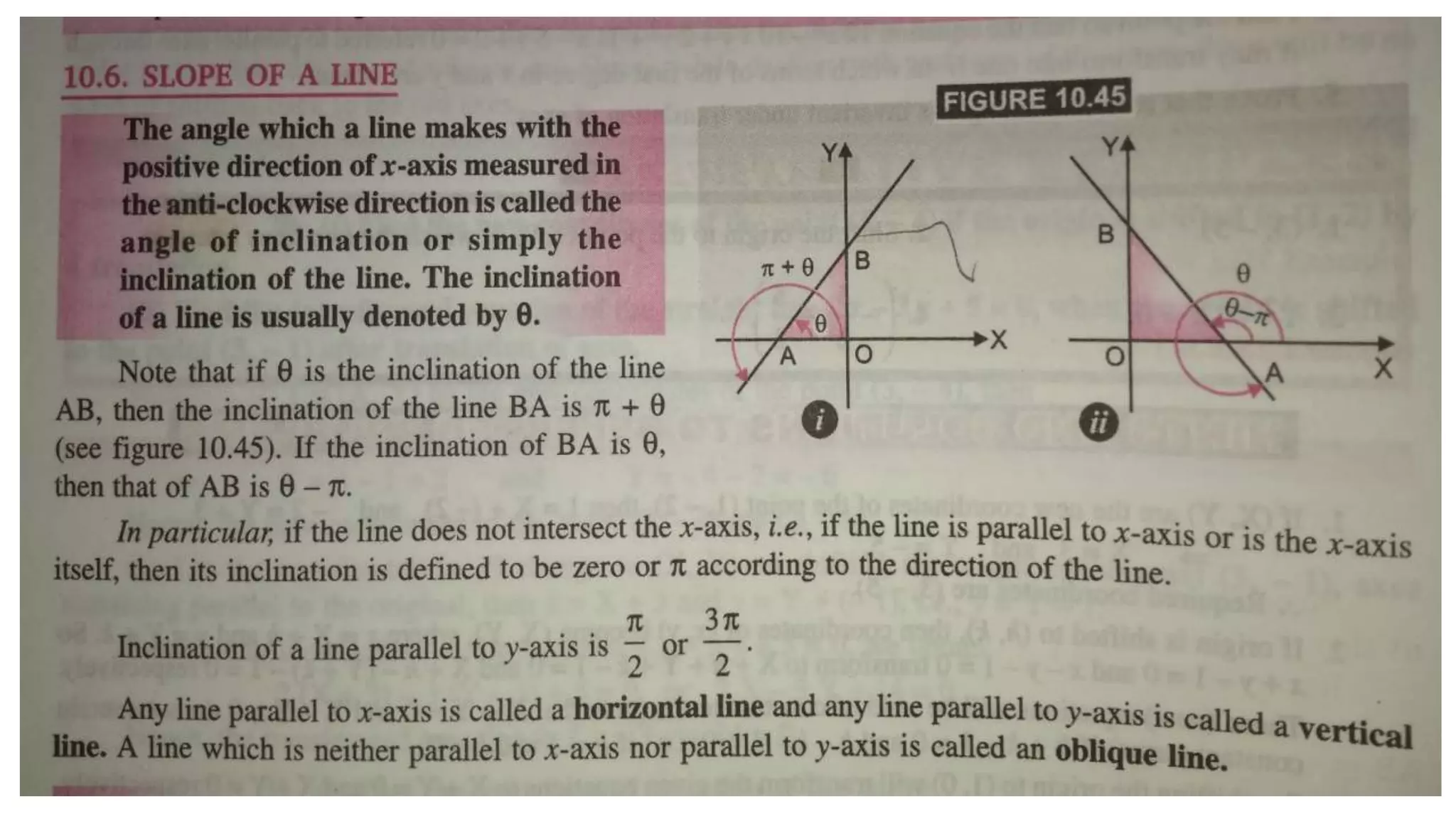
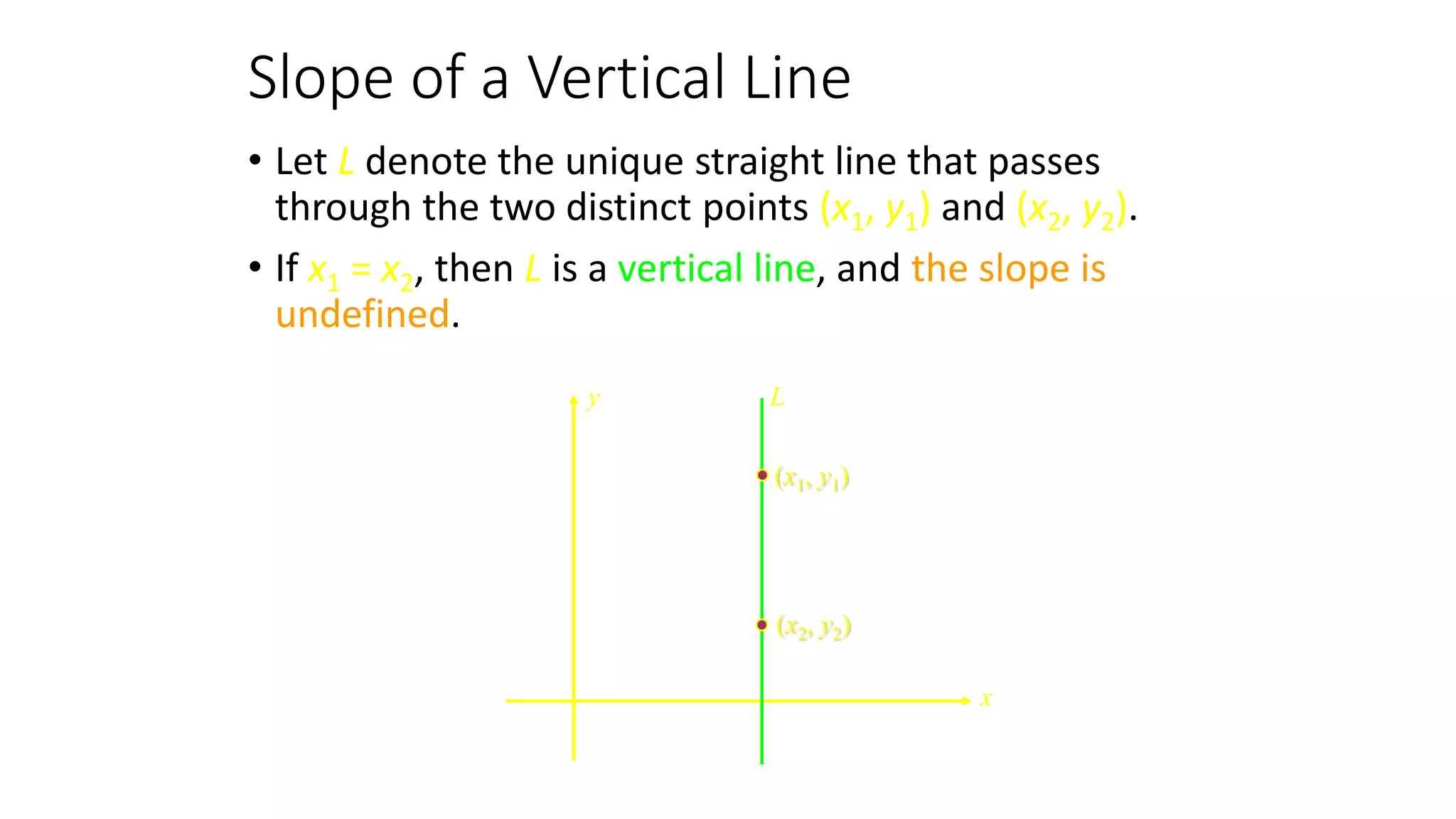
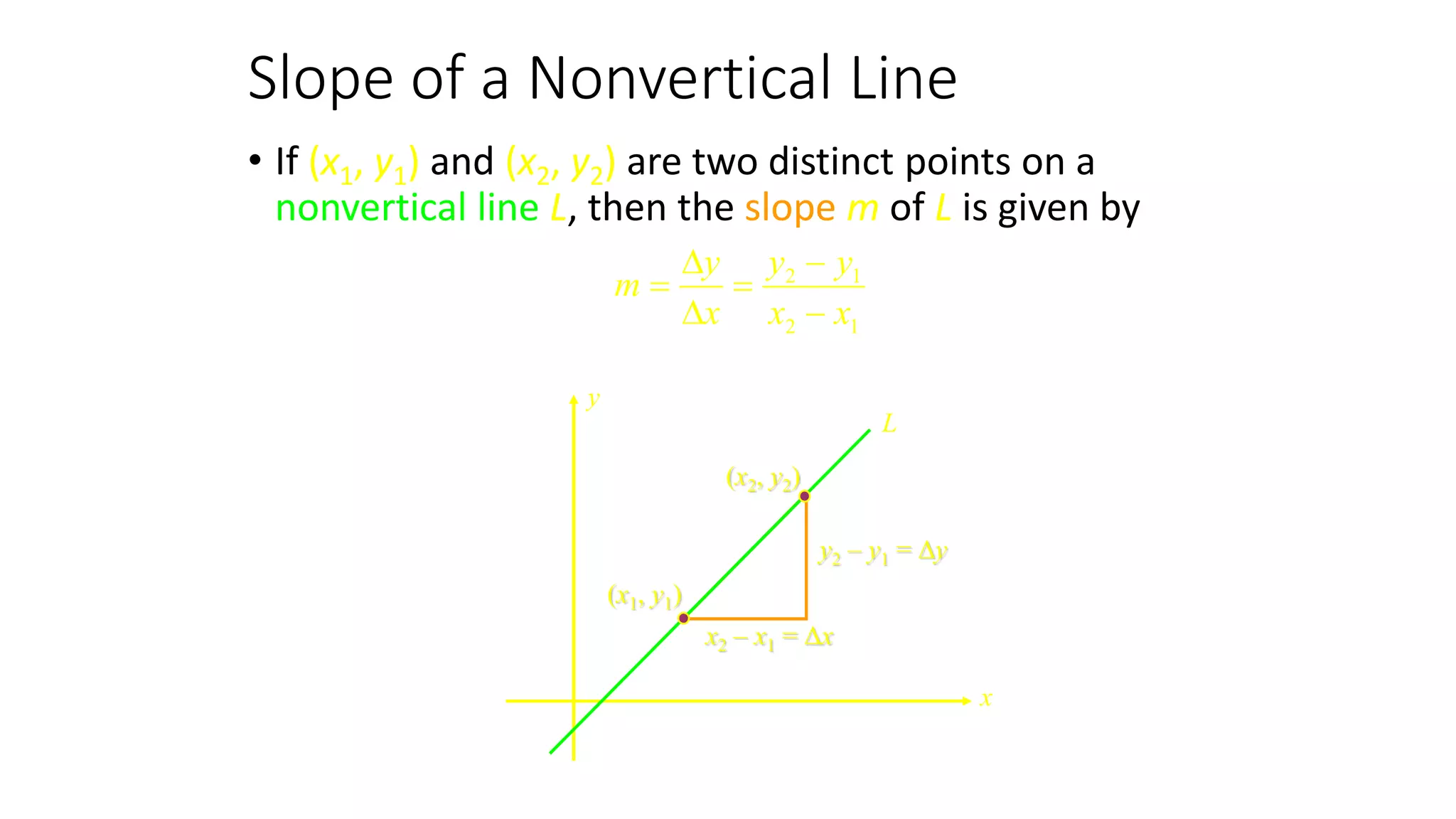
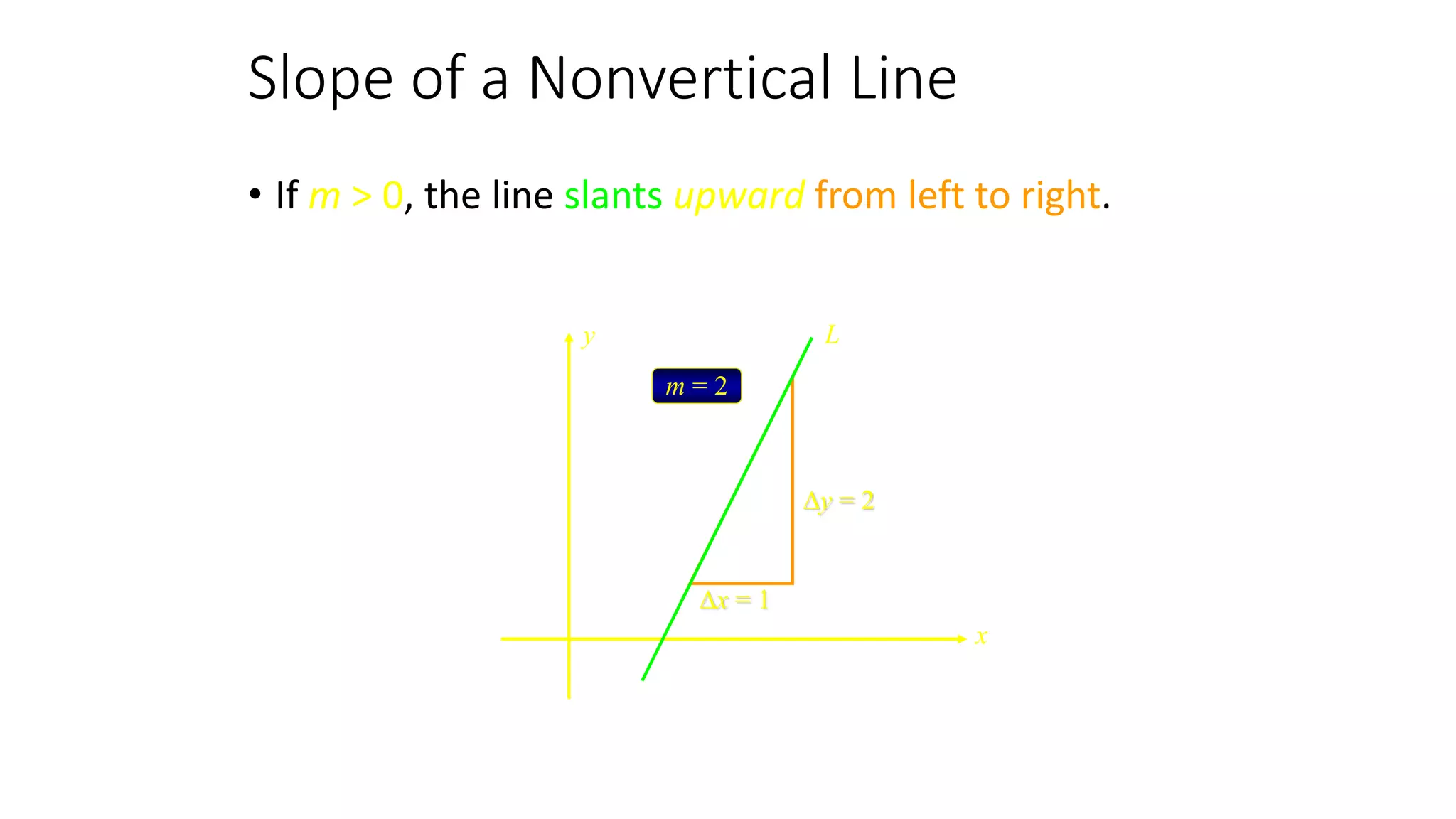
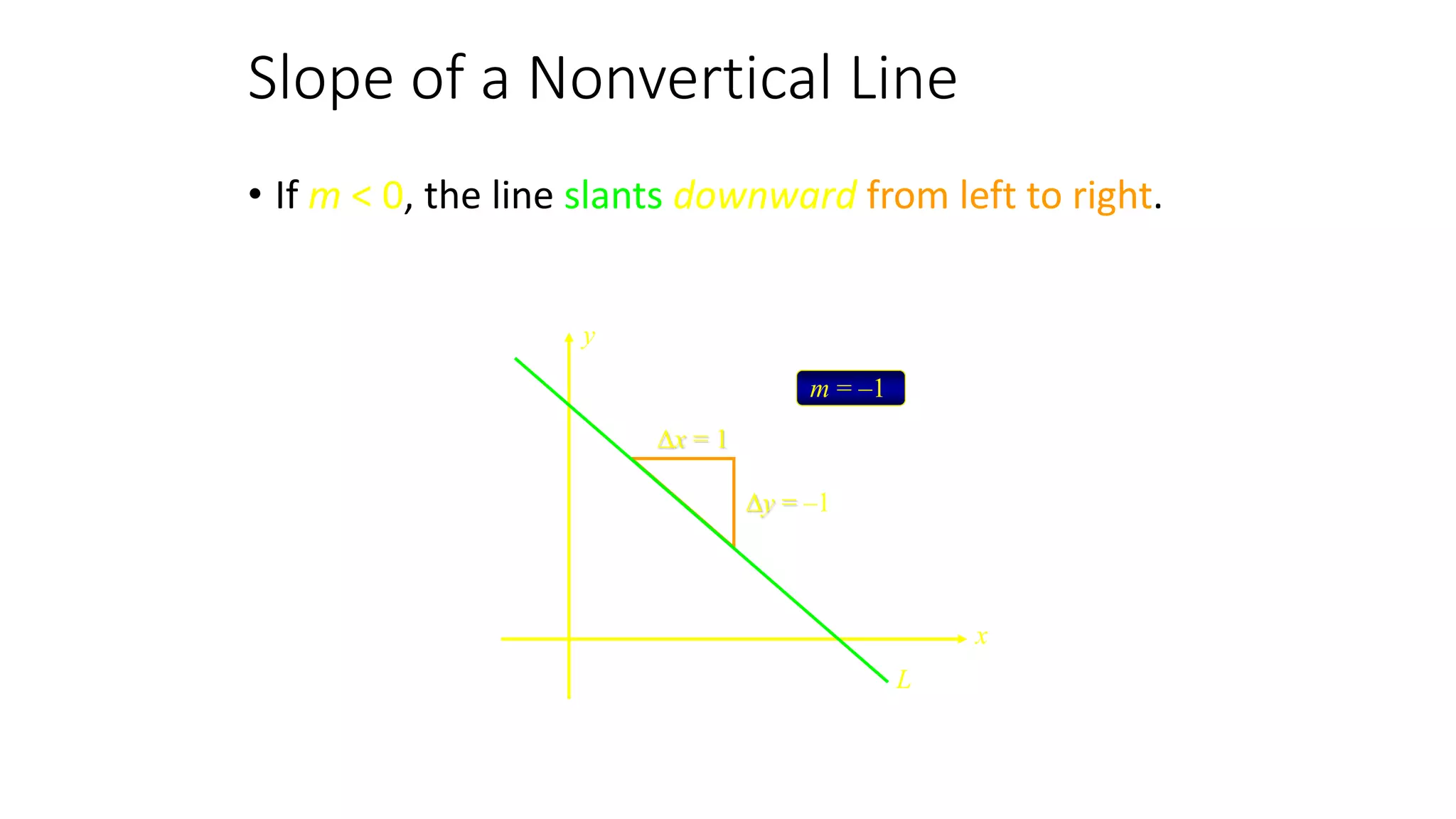
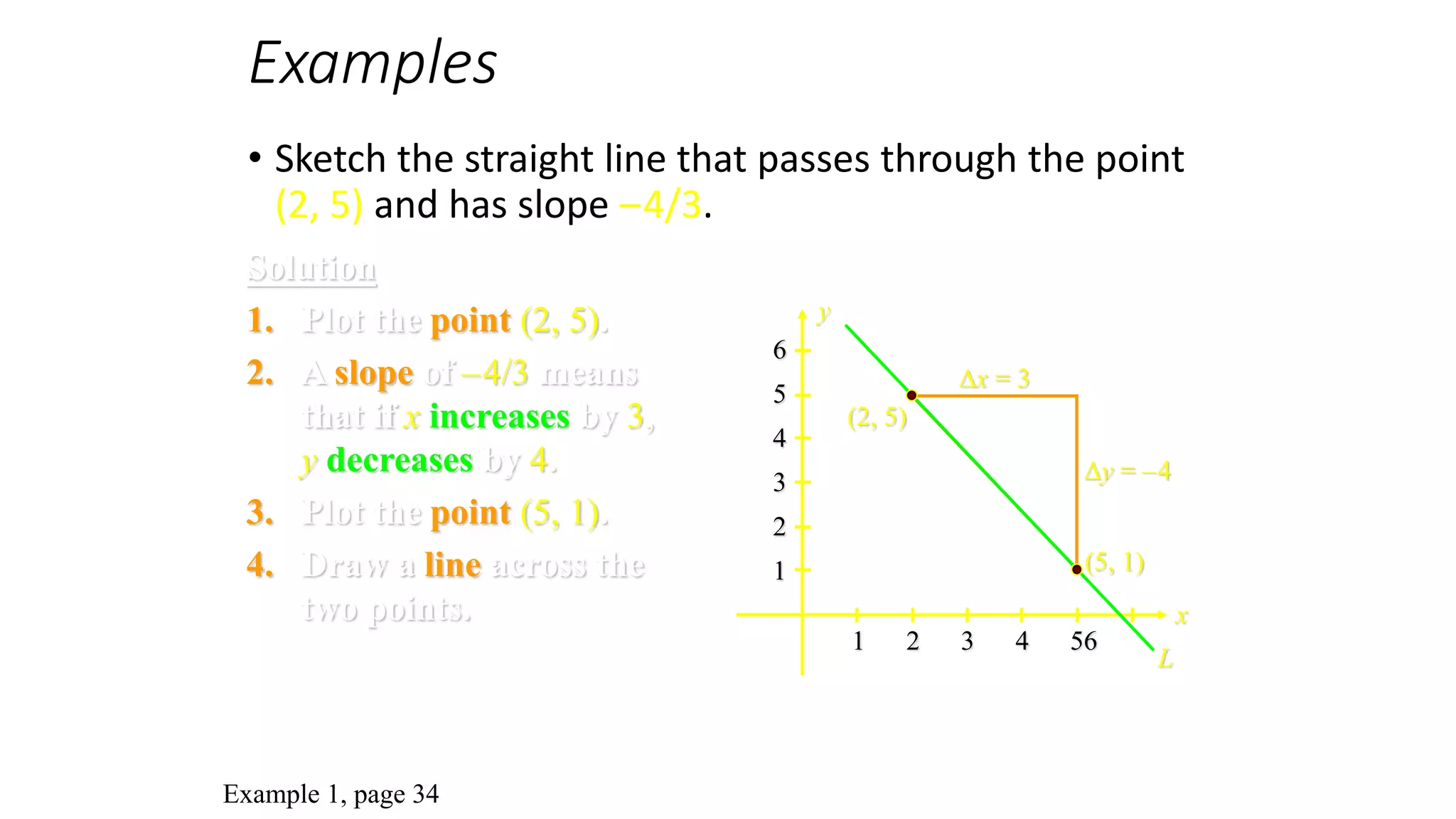
This document discusses slope and how to calculate it. It defines slope as the ratio of the rise over the run between two points on a line. A vertical line has an undefined slope since the run is zero. For a non-vertical line, the slope is calculated as the change in y-values divided by the change in x-values between two points. The slope indicates whether the line rises or falls from left to right. An example demonstrates how to sketch a line given its slope and a point.

9. Slope of a Vertical Line
• Let L denote the unique straight line that passes
through the two distinct points (x1, y1) and (x2, y2).
• If x1 = x2, then L is a vertical line, and the slope is
undefined.
(x1, y1)
(x2, y2)
y
x
L

10. Slope of a Nonvertical Line
• If (x1, y1) and (x2, y2) are two distinct points on a
nonvertical line L, then the slope m of L is given by
(x1, y1)
(x2, y2)
y
x
2 1
2 1
y y y
m
x x x
 
 
 
L
y2 – y1 = y
x2 – x1 = x

11. Slope of a Nonvertical Line
• If m > 0, the line slants upward from left to right.
y
x
L
y = 2
x = 1
m = 2

12. m = –1
Slope of a Nonvertical Line
• If m < 0, the line slants downward from left to right.
y
x
L
y = –1
x = 1

13. Examples
• Sketch the straight line that passes through the point
(2, 5) and has slope –4/3.
Solution
1. Plot the point (2, 5).
2. A slope of –4/3 means
that if x increases by 3,
y decreases by 4.
3. Plot the point (5, 1).
4. Draw a line across the
two points.
1 2 3 4 56
(2, 5)
y
x
L
y = –4
x = 3
6
5
4
3
2
1 (5, 1)
Example 1, page 34