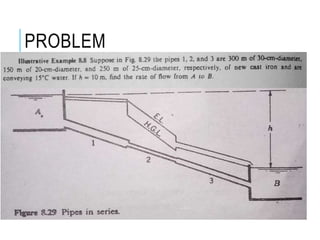
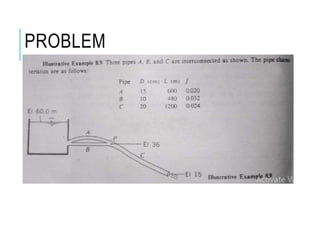
This document summarizes a lecture on pipe roughness and branching pipes. It discusses how pipe roughness affects friction factor and flow. As roughness increases, a pipe will transition from smooth to rough flow. The Moody chart graphs this relationship and is a standard tool for determining friction factor. The document also provides examples of calculating flow rates through pipes using friction factor and discusses how branching pipes affects flow.

1. FLUID MECHANICS-II
LEC #5: PIPE ROUGHNESS
AND BRANCHING PIPES
Dr. M.
Mubashir
Qureshi

2. PIPE ROUGHNESS
•There is no such thing in reality as a mathematically smooth surface.
•If the pipe will behave as though it is hydraulically
smooth, while
•if the pipe will behave as wholly rough.
•If the pipe will behave in a transitional mode

et 6

3. PIPE ROUGHNESS
• The friction is dependent not only upon the size and shape of the projections,
but also upon their distribution or spacing.
• Nikuradse, Experiment
• Absolute roughness, e.
• f = (NR, e/D). The term (e/D is known as the relative roughness)
This equation applies to any pipe as long i.e. flow is known as smooth flow.
The equation has been found to be reliable for smooth pipes for all values of NR
over 4,000.

et 6

4. PIPE ROUGHNESS
• Blasius has shown that for Reynolds numbers between 3,000 and 100,000 the
friction factor for a very smooth pipe may be expressed approximately as;
• He also found that over this range of Reynolds numbers the
velocity profile in a smooth pipe is closely approximated by the
expression
where y = r0 - r, the distance from the pipe wall.
• This equation is commonly referred to as the seventh-root law for turbulent-
velocity distribution.
• Though it is not absolutely accurate, it is useful because it is easy to work with
mathematically. At Reynolds numbers above 100,000 a somewhat smaller
exponent must be used to give good results.

5. PIPE ROUGHNESS
• At high Reynolds numbers becomes smaller. If , it has been found
that the pipe behaves as a wholly rough pipe; i.e., its friction factor is
independent of the Reynolds number.
• For such a case Von Karman found that the friction factor could be expressed as
• For , neither smooth flow nor wholly rough flow,
Colebrook found that;
t

6. THE MOODY CHART
 In 1939 to cover the transitionally rough range, Colebrook
combined the smooth wall and fully rough relations into a clever
interpolation formula:.
 This is the accepted design formula for turbulent friction. It was
plotted in 1944 by Moody into what is now called the Moody chart for
pipe friction.

7. THE MOODY CHART

8. RECOMMENDED ROUGHNESS
VALUES FOR COMMERCIAL
DUCTS

9. THE MOODY CHART
Moody chart is probably the most famous and useful figure in fluid
mechanics. Some of its properties are;
 It is accurate to 15 percent for design calculations over the full range shown in Fig.
 It can be used for circular and noncircular pipe flows and for open-channel flows.
 The data can even be adapted as an approximation to boundary layer flows
 The shaded area in the Moody chart indicates the range where transition from laminar
to turbulent flow occurs.
 There are no reliable friction factors in this range, 2000 < Red, < 4000.
 Notice that the roughness curves are nearly horizontal in the fully rough regime to the
right of the dashed line.

10. PROBLEM
Example 8.4:Water at 20°C flows in a 50-cm-diameter welded-steel pipe. If the
energy gradient is 0.006, determine the flow rate. Find also the nominal thickness of
the viscous sublayer.

11. PROBLEM

12. PROBLEM
Example 8.6:In figure 8.23, suppose that pipeline of preceding example is now fitted
with a nozzle at the end (8.23b) which discharges a jet 6.5cm dia and with a loss
coefficient of 0.11. Find flow rate.

13. PROBLEM
P
4.5-
m
3-
m
Power=15K
W

14. PROBLEM

15. PROBLEM

16. BRANCHING PIPES

17. ASSIGNMENT 1
Problem 1
Problem 2
Problem 3 Two pipes one square and one circular have same
cross-sectional area. Which has the larger hydraulic radius and by
what percentage?

18. ASSIGNMENT 1
Problem 4
Problem 5
Problem 6

19. ASSIGNMENT 1
Problem 7
Problem 8
Problem 9

20. ASSIGNMENT 1
Problem 10
Problem 11
Problem 12

21. ASSIGNMENT 1
Problem 13
Problem 14
Problem 15

22. ASSIGNMENT 1
Problem 16
Problem 17
Problem 18

23. ASSIGNMENT 1
Problem 19 (use MS Excel to solve)
Problem 20
Problem 21