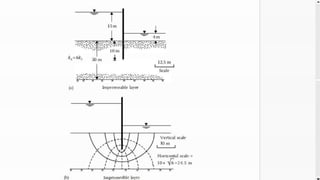
This document discusses constructing flow nets to analyze seepage in anisotropic soils where permeability varies in horizontal and vertical directions. It provides the procedure for plotting flow nets in anisotropic soils by transforming the horizontal scale based on the ratio of horizontal to vertical permeability. The steps include: 1) adopting vertical and transformed horizontal scales, 2) plotting the cross-section using these scales, 3) drawing the flow net in the transformed plane, and 4) replotting the flow net in the natural scale. An example problem applies these steps to construct the flow net for a sheet pile structure with a given permeability ratio and calculates the equivalent permeability.

1. FLOW NETS I N A N I S O T R O P I C MATERIAL
In developing the procedure described for plotting flow nets, we
assumed that the permeable layer is isotropic, that is, krona =k,ate = k.
Let us now consider the case of constructing flow nets for seepage through
soils that show anisotropy with respect to permeability. For two-dimensional
flow problems, we refer to Equation
where
k , = k , o n t a l
k , = k e a t
This equation can be rewritten as
previously
:
(Ref. BM Das)

2. l
i
Let x'=/k./Ik,x, then
[x' is the transformed coordinate]

3. Substituting
which governs the
flow in isotropic soils and should represent two sets of orthogonal lines
in the x'z plane. The steps for construction of a flow net in an anisotropic
medium are as follows:
1. T
o plot the section of the hydraulic structure, adopt a vertical scale.
2. Determine /k./k, = lk a l % o a t ­
3. Adopt a horizontal scale such that
4. With the scales adopted in steps 1 and 3, plot the cross section of the
structure.
5. Draw the flow net for the transformed section plotted in step 4 in the
the expression of x' , we get
Above equation is same as Laplace eqn.
x dimension will be modified to x'.

4. I I C I H I A I H I I I d I ( O I I C IOI SCCpd4C L I 1 I O U 4 I I 1 O L I U p I K S U 1 I S ,
6. Calculate the rate of seepage as
Example
A dam section is shown in Figure 7.9a. The coefficients of permeability
of the permeable layer in the vertical and horizontal directions are
2 x 1 0 - a n d 4 10- mm/s, respectively. Draw a flow net and calculate
the seepage loss of the dam in m/(day·m).
Solution
From the given data
where, sqrt.(kx . kz) is the equvt permeability ke. Studemt is asked to derive it.
The above equation is same in form as derived for Isotropic Soil, except K is replaced by Ke.

5. . h] m e · l Advanced Soit Mechanics; Fifth Edition Nitro P
r
o - 6 X
File Convert Review Page Layout Forms Share Erase Protect Help login
U m
m
h T ./ a [! (
5
~ 5
A
c
[@Rotate·
3 ·l
I, tat Er beete
zoom
Select T
y
p
e Qui«Sign Request PD
F Combine T
o T
o Highlight nsert
[ 6t
r
a
ct
F
i
n
d A
d
d Customize
T
e
t Signature word D
e
l Note Tools
Tools Create Convert R
evi
ew P
a
g
e layout Document Favorite Tools
D
x
G
I cover •
£
I H
a
it T
i
l
e
I mute Page
l copyright Page
l Dedication
I contents
I Preface
[ Acknowledgments
I Author
a [] 1. soil aggregate, plasticity,
and classification
[ Advanced_Soit_Mechanics_Fifth_Edi.. X
k,
and h
2x10mm/s 1.728 m/day
•
•
k, =4x10mm/s = 3.456 m/day
10 m. For drawing the flow net,
8 [ 2 stresses and strains:
Horizontal
Elastic equilibrium
ffi [] 3 . stresses and
displacements I
n a soil mass:
Two-dimensional problems
8 []4. stresses and
displacements i
n a soil mass:
Three-dimensional problems
8 [ 5 pore w
a
t
e
r Pressure d
u
e
t
o undrained loading
ffi ] 6
. Permeability
a In7. seepage
a le. consolidation
8 [9. shear strength o
f soils
gen
a [ 1o. E
l
a
s
t
i
c settlement o
f
0 shallow foundations
z e [ 1 . consolidation settlement
I ◄ ◄ 298 03
2
1 O
F 7
3
5
► I o 0
II P Search
0 0 g a g ­ + 213%
­
dimension is reduced by Sqrt.2

6. I0 m
Permeable
layer 12.5 m
(a) Impermeable layer
10 m
-
'
1.
0 :
f
'
f
'
,
,
'
,
'
,
' ' '
f
'
1.
0
' '
'
f
' '
f
'
'
I 05
'
'
' '
$
' '
'
' ' ' ' ' ' '
'
Horizontal scale = 12.5 V-17.68 m
(
b
) Vertical scale = 12.5 m
fi
g
u
r
e 7.9 Construction of flow net under a dam: (a) section of the dam; (b) flow net.

7. On the basis of this, the damsection is replotted, and the tlow net drawn
as in Egure 79h. The rate of seepage is given by q = Jk,k,h(NIN).
From Figure7.9b, N
, = 8 and N
, = 2.5 (the lowermost flow channel has
a width-to-length ratio of 0.5). So
q =4(1.728)63.456)010)02.5/8) = 7.637 m'/(day ·m)
Example 7.4
A single row of sheet pile structure is shown in Figure 7.10a. Draw a
flow net for the transformed section. Replot this flow net in the natu­
ral scale also. The relationship between the permeabilities is given as
k, = 6k_.
Solution
For the transformed section
· e
k,
Horizontal dimension actual dimension
actual horizontal dimension.

8. •
1 5 m
4 m
+
2
0 m
(
a
) Impermeable l
a
y
e
r
(
b
)
==a
- -
Vertical scale
,
­ IO m
,
-
, ,
'
'
,
'
+
' ' '
f
f
'
'
Horizontal scale =
'
'
' ' 1 o » 6=24.5 m
f
f
' ' '
f
'
f
' '
Impermeable layer

9. '
'
---
---
--
-----
--- ---
.
----
-
-
,
­
10 m
(
c
) Scale
Fi
g
u
r
e 740 Flow net construction in anisotropic soil: (a) sheet pile structure; (
b
) flow
net in transformed scale; (
c
) flow net in natural scale.
Ke = sqrt. (Kx.Kz) .... prove it.
In previous slide obtain h, z and hp at points A, B and C
HT: