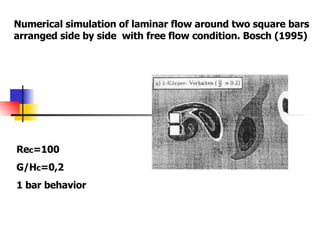
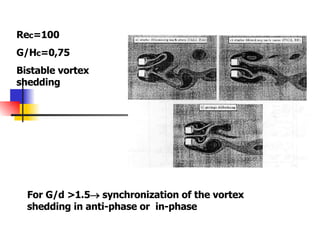
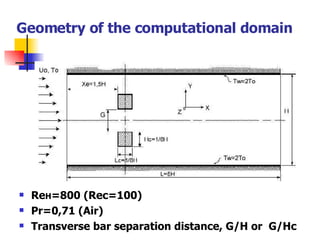
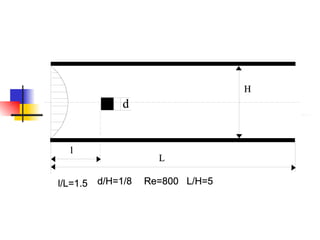
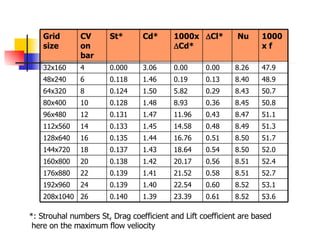
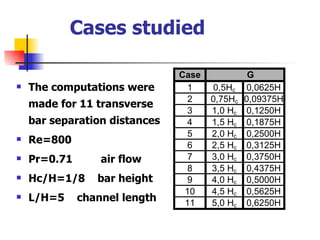
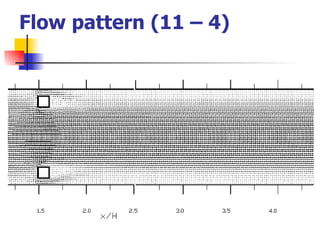
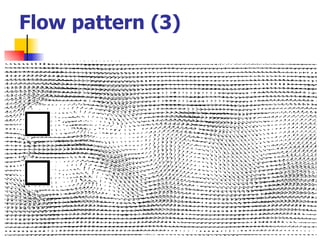
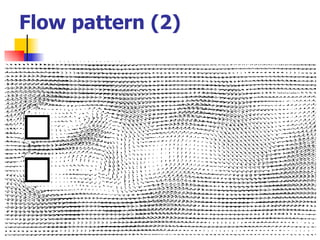
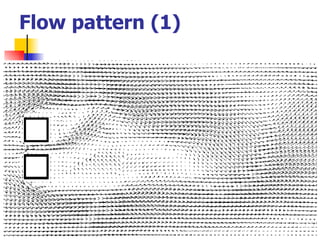
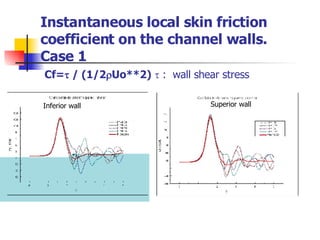
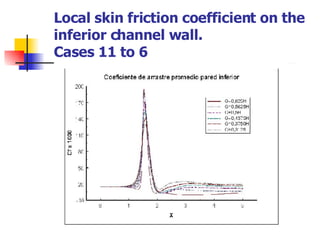
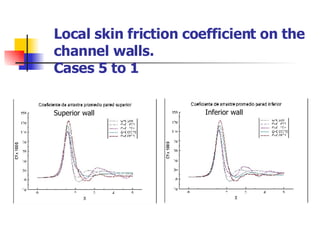
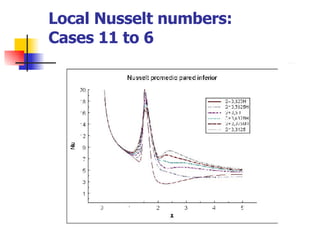
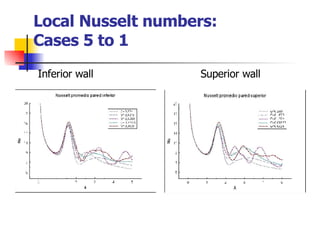
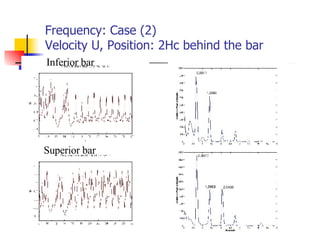
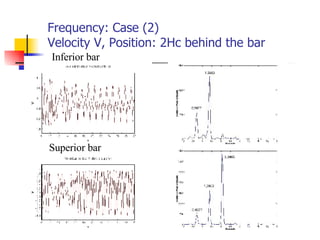
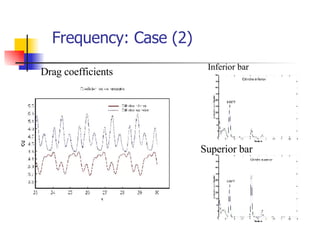
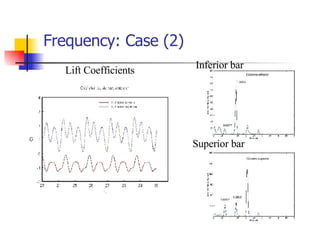
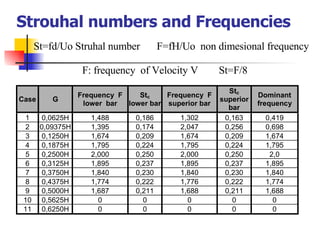
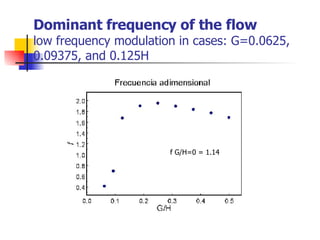
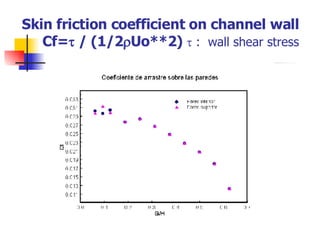
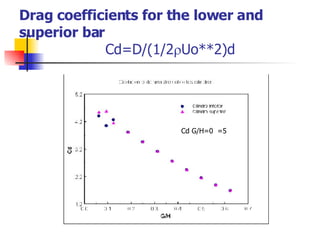
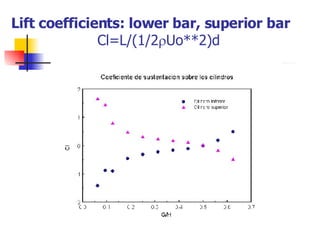
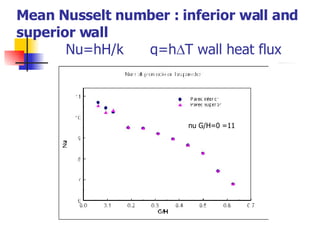
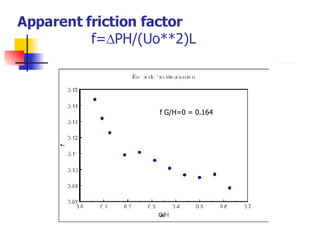
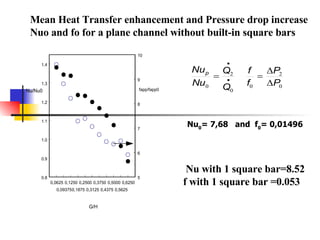
Professor Alvaro Valencia from the University of Chile studied laminar unsteady flow and heat transfer in a confined channel with square bars arranged side by side through numerical simulation. The study categorized flow patterns into three regimes based on the bar separation distance and examined the effects on pressure drop, heat transfer, and vortex shedding frequency. Results showed that local and overall heat transfer on channel walls increased significantly due to unsteady vortex shedding induced by the bars.

1. Laminar unsteady flow and heat transfer in confined channel flow past square bars arranged side by side Professor Alvaro Valencia Universidad de Chile Department of Mechanical Engineering

3. Turbulent flow near a wall, Re=22000, experimental results, Bosch ( 1995) Numerical results, k-  turbulence model

4. Anti-phase and in-phase vortex shedding around cylinders Re=200 G/d=2.4 Williamson, (1985)

6. Numerical simulation of laminar flow around two square bars arranged side by side with free flow condition. Bosch (1995) Re c =100 G/H c =0,2 1 bar behavior

7. Re c =100 G/H c =0,75 Bistable vortex shedding For G/d >1.5  synchronization of the vortex shedding in anti-phase or in-phase

15. *: Strouhal numbers St, Drag coefficient and Lift coefficient are based here on the maximum flow veliocity 53.6 8.52 0.61 23.39 1.39 0.140 26 208x1040 53.1 8.52 0.60 22.54 1.40 0.139 24 192x960 52.7 8.51 0.58 21.52 1.41 0.139 22 176x880 52.4 8.51 0.56 20.17 1.42 0.138 20 160x800 52.0 8.50 0.54 18.64 1.43 0.137 18 144x720 51.7 8.50 0.51 16.76 1.44 0.135 16 128x640 51.3 8.49 0.48 14.58 1.45 0.133 14 112x560 51.1 8.47 0.43 11.96 1.47 0.131 12 96x480 50.8 8.45 0.36 8.93 1.48 0.128 10 80x400 50.7 8.43 0.29 5.82 1.50 0.124 8 64x320 48.9 8.40 0.13 0.19 1.46 0.118 6 48x240 47.9 8.26 0.00 0.00 3.06 0.000 4 32x160 1000x f Nu  Cl* 1000x  Cd* Cd* St* CV on bar Grid size

16. Grid size

17. Grid size

18. Grid size

21. Flow pattern (11 – 4)

22. Flow pattern (3)

23. Flow pattern (2)

24. Flow pattern (1)

25. Instantaneous temperature field Case 1

26. Instantaneous local skin friction coefficient on the channel walls. Case 1 Cf=  / (1/2  Uo**2)  : wall shear stress Inferior wall Superior wall

27. Local skin friction coefficient on the inferior channel wall. Cases 11 to 6

28. Local skin friction coefficient on the channel walls. Cases 5 to 1 Superior wall Inferior wall

29. Local Nusselt numbers: Cases 11 to 6

30. Local Nusselt numbers: Cases 5 to 1 Inferior wall Superior wall

31. Frequency: Case (2) Velocity U, Position: 2Hc behind the bar Inferior bar Superior bar

32. Frequency: Case (2) Velocity V, Position: 2Hc behind the bar Inferior bar Superior bar

33. Frequency: Case (2) Drag coefficients Inferior bar Superior bar

34. Frequency: Case (2) Lift Coefficients Inferior bar Superior bar

35. Strouhal numbers and Frequencies St=fd/Uo Struhal number F=fH/Uo non dimesional frequency F: frequency of Velocity V St=F/8

36. Dominant frequency of the flow low frequency modulation in cases: G=0.0625, 0.09375, and 0.125H f G/H=0 = 1.14

37. Skin friction coefficient on channel wall Cf=  / (1/2  Uo**2)  : wall shear stress

38. Drag coefficients for the lower and superior bar Cd=D/(1/2  Uo**2)d Cd G/H=0 =5

39. Lift coefficients: lower bar, superior bar Cl=L/(1/2  Uo**2)d

40. Mean Nusselt number : inferior wall and superior wall Nu=hH/k q=h  T wall heat flux nu G/H=0 =11

41. Apparent friction factor f=  PH/(Uo**2)L f G/H=0 = 0.164

42. Mean Heat Transfer enhancement and Pressure drop increase Nuo and fo for a plane channel without built-in square bars Nu 0 = 7,68 and f 0 = 0,01496 Nu with 1 square bar=8.52 f with 1 square bar =0.053

46. References [1] H. Suzuki, Y. Inoue, T. Nishimura, K. Fukutani, k. Suzuki, Unsteady flow in a channel obstructed by a square rod (crisscross motion of vortex). International Journal of Heat and Fluid Flow 14 (1993) 2-9. [2] A. K. Saha, K. Muralidhar, G. Biswas, Transition and chaos in two-dimensional flow past a square cylinder, Journal of Engineering Mechanics, 126, (2000), 523-532. [3] M. Breuer, J. Bernsdorf, T. Zeiser, F. Durst, Accurate computations of the laminar flow past a square cylinder based on two different methods: lattice-Boltzmann and finite-volume, International Journal of Heat and Fluid Flow, 21, (2000), 186-196. [4] J. L Rosales, A. Ortega, J.A.C. Humphrey, A numerical simulation of the convective heat transfer in confined channel flow past square cylinders: comparison of inline and offset tandem pairs, International Journal of Heat and Mass Transfer, 44, (2001), 587-603. [5] K. Tatsutani, R. Devarakonda, J.A.C. Humphrey, Unsteady flow and heat transfer for cylinder pairs in a channel, International Journal of Heat and Mass Transfer, 36, (1993), 3311-3328. [6] A. Valencia, Numerical study of self-sustained oscillatory flows and heat transfer in channels with a tandem of transverse vortex generators, Heat and Mass Transfer, 33, (1998), 465-470. [7] D. Sumner, S.J. Price, M.P. Païdoussis, Flow-pattern identification for two staggered circular cylinders in cross-flow, Journal of Fluid Mechanics, 411, (2000), 263-303. [8] C.H.K. Williamson, Evolution of a single wake behind a pair of bluff bodies, Journal of Fluid Mechanics, 159, (1985), 1-18. [9] J.J. Miau, H.B. Wang, J.H. Chou, Flopping phenomenon of flow behind two plates placed side-by-side normal to the flow direction, Fluid Dynamics Research, 17, (1996), 311-328. [10] M. Hayashi, A. Sakurai, Wake interference of a row of normal flat plates arranged side by side in a uniform flow, Journal of Fluid Mechanics, 164, (1986), 1-25. [11] S.C. Luo, L.L. Li, D.A. Shah, Aerodynamic stability of the downstream of two tandem square-section cylinders, Journal of Wind Engineering and Industrial Aerodynamics, 79, (1999), 79-103. [12] G. Bosch, Experimentelle und theoretische Untersuchung der instationären Strömung um zylindrische Strukturen, Ph.D. Dissertation, Universität Fridericiana zu Karlsruhe, Germany, (1995). [13] S. Patankar, Numerical heat transfer and fluid flow, Hemisphere Publishing Co., New York, (1980). [14] J.P. van Doormaal, G.D. Raithby, Enhancements of the SIMPLE method for predicting incompressible fluid flows. Numerical Heat Transfer, 7, (1984), 147-163.