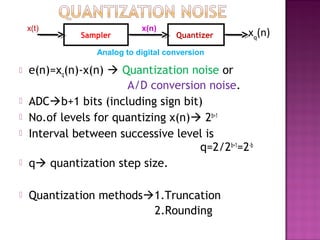
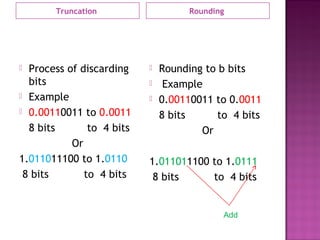
1. DSP algorithms are realized using special or general purpose digital hardware where numbers are stored using a finite number of bits. Quantization errors are introduced during truncation or rounding of coefficients and numbers. 2. There are three main types of quantization errors: input quantization error from A/D conversion, product quantization error from multiplier outputs being rounded to a finite number of bits, and coefficient quantization error that deviates the frequency response from the desired response. 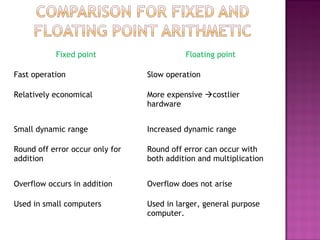3. Fixed point and floating point representations are used to represent numbers in digital computers, with fixed point using a fixed binary point and floating point having a variable binary point to increase dynamic range at the cost of more complex hardware.

1. Prepared by
V.Thamizharasan
Assistant professor
Department of ECE
Erode Sengunthar Engineering College

2.  DSP algorithms realized special/general
purpose digital hardware.
 Numbers stored in finite length register.
 Coefficients and numbers are quantized by
truncation or rounding
 Errors are created due truncation or rounding

3.  1. Input quantization error.
conversion of continuous time input signal into
digital value  error.
It arises due to representation of the input signal
by a fixed No. of digits in A/D conversion.
2. Product Quantization Error.
It arises at the output of multiplier.
Multiplier need Two numbers have a ‘b’ bits
result of multiplication 2b bits.
B bit register is used in processor.
Multiplier output must be rounded or truncated to
b bits  it produces error.

4. 3.Coefficient quantization error
Fitter coefficients compared to infinite precision theory.
Frequency response is deviated from desired response.
If the poles of the desired filter close to unit circle
Deviated response filter may be poles lies just
outside of unit circle
Leading instability.

5. Number
=3*101
+0*100
+2*10-1
+8*10-2
+5*10-3
Binary number system r=2 0 to 1
Where r  radix
Decimal number system r=10 0 to 9
=1*22
+1*21
+0*20
+0*2-1
+1*2-2
+

6. Convert the decimal number to binary form.

7. Three forms that are used in digital computers
1.Fixed point representation
2.Floating point representation
3.Block floating point representation
Fixed point representation
Position of the binary point is fixed.
01.1100
Integer part
Fractional part

8. 1. sign-magnitude form
Most significant bit(MSB)
Set to 1 set to 0
Negative sign Positive sign
-1.75=11.1100 +1.75=01.1100
(1.75)10
(1)101
0.75100.75*2=1.501
0.50*2=1.001
0*0 =0.000
0*0 =0.000

9.  +ve number  Represented same as that
sign Magnitude form.
(+0.875)10(0.111000)2
0.875100.875*2=1.751
0.75*2=1.501
0.50*2=1.001
0*0 =0.000
0*0 =0.000
0*0 =0.000
(-0.875)10
0.875100.111000
1.000111 complement of each bit
(-0.875)10=(1.000111)2

10.  +ve number  Represented as same sign
Magnitude form.
(+0.875)10(0.111000)2
0.875100.875*2=1.751
0.75*2=1.501
0.50*2=1.001
0*0 =0.000
0*0 =0.000
0*0 =0.000
(-0.875)10
0.875100.111000
1.000111 complement of each bit
1add one
(-0.875)10=(1.000111)2

11. Addition of two fixed
point numbers
Causes overflow
(0.5)10+(0.125)10
(0.5)10 0.100
(0.125)10 0.001
0.101
Sign bit
(0.101)2 (0.625)10
(0.5)10+(0.625)10
(0.5)10 0.100
(0.625)10 0.101
1.001
Sign bit
(1.001)2 (-0.125)10
To add (0.5)10+(0.125)10
Assume total no. of bits =b+1=3+1=4 ( including sign bit)
Sum cant be represented by b
bits overflow occur

12.  0.5 0.100
-0.25 1.110
10.010
Neglect carry bit
0.0100.25
*****************************
0.25 0.010
-0.5 1.100
1.110
Carry not generated
1.1101.110
0.001
1
0.0100.25 -0.25
0.25 0.010
1.1011’s
complement
1add 1
-0.251.110 2’s complement
*****************************
0.5 0.100
1.011 1’s
complement
1 add 1
-0.5 1.100 2’s complement
Subtract a).0.25 from 0.5 & b).0.5 from 0.25
Include - sign

13.  Sign and magnitude
components  separated
 b bit multiplied with
Another b bit .
 Product 2b bits.
 B bitsbi+bf
 product b=2bi+2bf
 Overflow can never occur.
 (11)2*(11)2=(1001)2
 (0.1001)2*(0.0011)2
4-bits 4 bits
=(0.00011011)2
8 bits

14.  +ve number  F=2C
.M
 M Mantissa 0.5 to 1 C Exponent
Decimal
Number
Floating point
representations
4.5 23
*0.5625 2011
*0.1001
1.5 21
*0.75 2001
*0.1100
6.5 ? ?
0.625 ? ?
Floating point multiplication
F1=2C1
*M1 F2=2C2
*M2
Product=F1*F2=F3=(M1*M2)2C1+C2
M1*M2Range 0.25 to 1

15. (1.5)10*(1.25)10
(1.5)10 21
*0.75 =2001
*0.1100
(1.25)1021
*0.625 = 2001
*0.1010
(1.5)10*(1.25)10=(2001
*0.1100)( 2001
*0.1010)
=2010
(0.110*0.1010)
=2010
*0.01111

16. Fixed point Floating point
Fast operation Slow operation
Relatively economical More expensive costlier
hardware
Small dynamic range Increased dynamic range
Round off error occur only for
addition
Round off error can occur with
both addition and multiplication
Overflow occurs in addition Overflow does not arise
Used in small computers Used in larger, general purpose
computer.

17.  Set of signals  divided into blocks
 Each block same exponent
 With in each block  uses fixed point arithmetic
 Only one exponent per block
 Saving the memory
 Mostly suitable for FFT flow graphs & in digital
audio applications.

18.  e(n)=xq(n)-x(n)  Quantization noise or
A/D conversion noise.
 ADCb+1 bits (including sign bit)
 No.of levels for quantizing x(n) 2b+1
 Interval between successive level is
q=2/2b+1
=2-b
 q quantization step size.
 Quantization methods1.Truncation
2.Rounding
Sampler Quantizer
x(t) x(n)
xq
(n)
Analog to digital conversion

19. Truncation Rounding
 Process of discarding
bits
 Example
 0.00110011 to 0.0011
8 bits to 4 bits
Or
1.011011100 to 1.0110
8 bits to 4 bits
 Rounding to b bits
 Example
 0.00110011 to 0.0011
8 bits to 4 bits
Or
1.011011100 to 1.0111
8 bits to 4 bits
Add

20. Type of
Quantization
Type of
arithmetic
Fixed point
number
Floating point number
Rounding Sign-
magnitude,
1’s
complement ,
2’s
complement
Truncati
on
2’s
complement
Sign-
magnitude,
1’s
complement ,