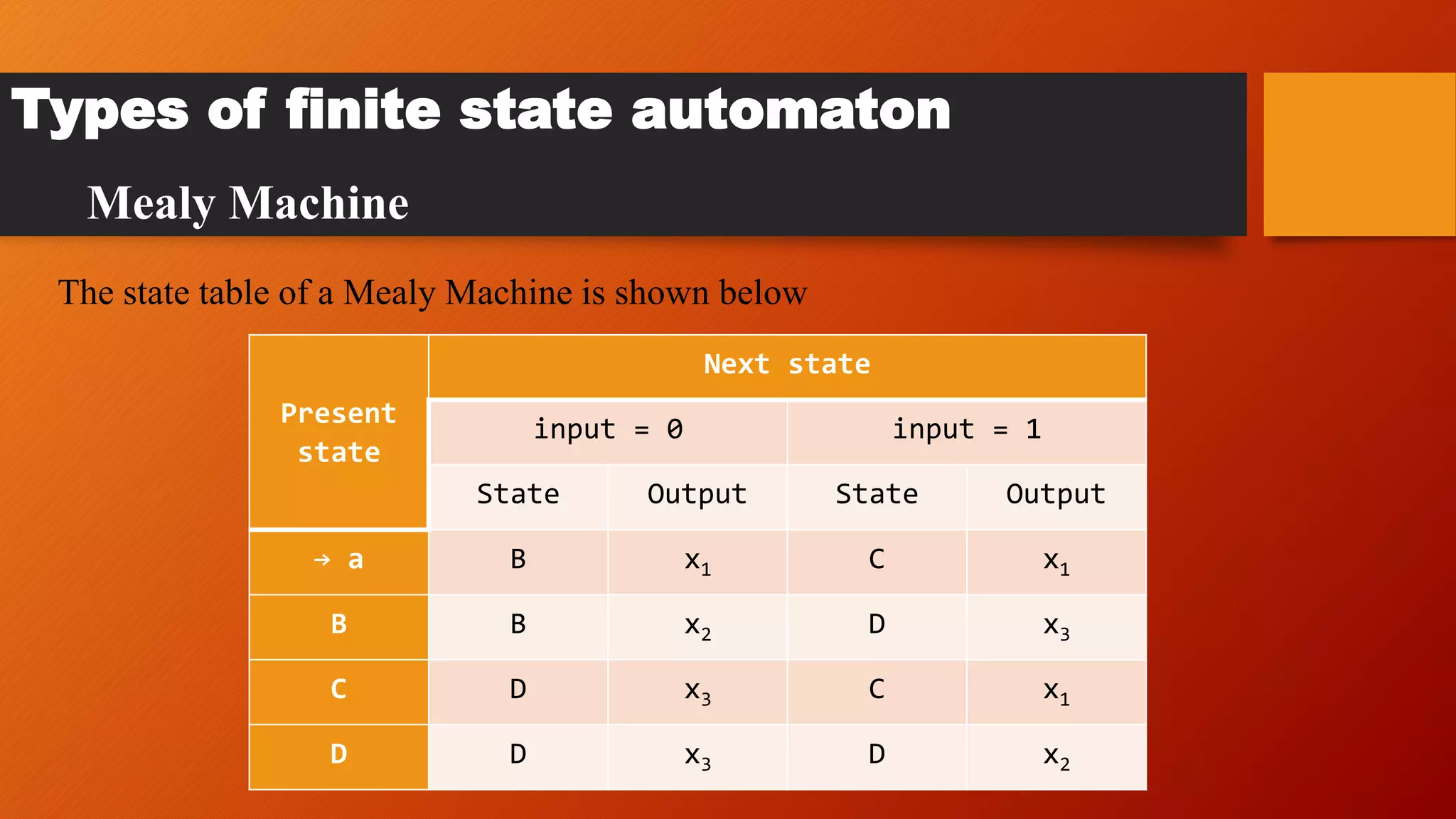
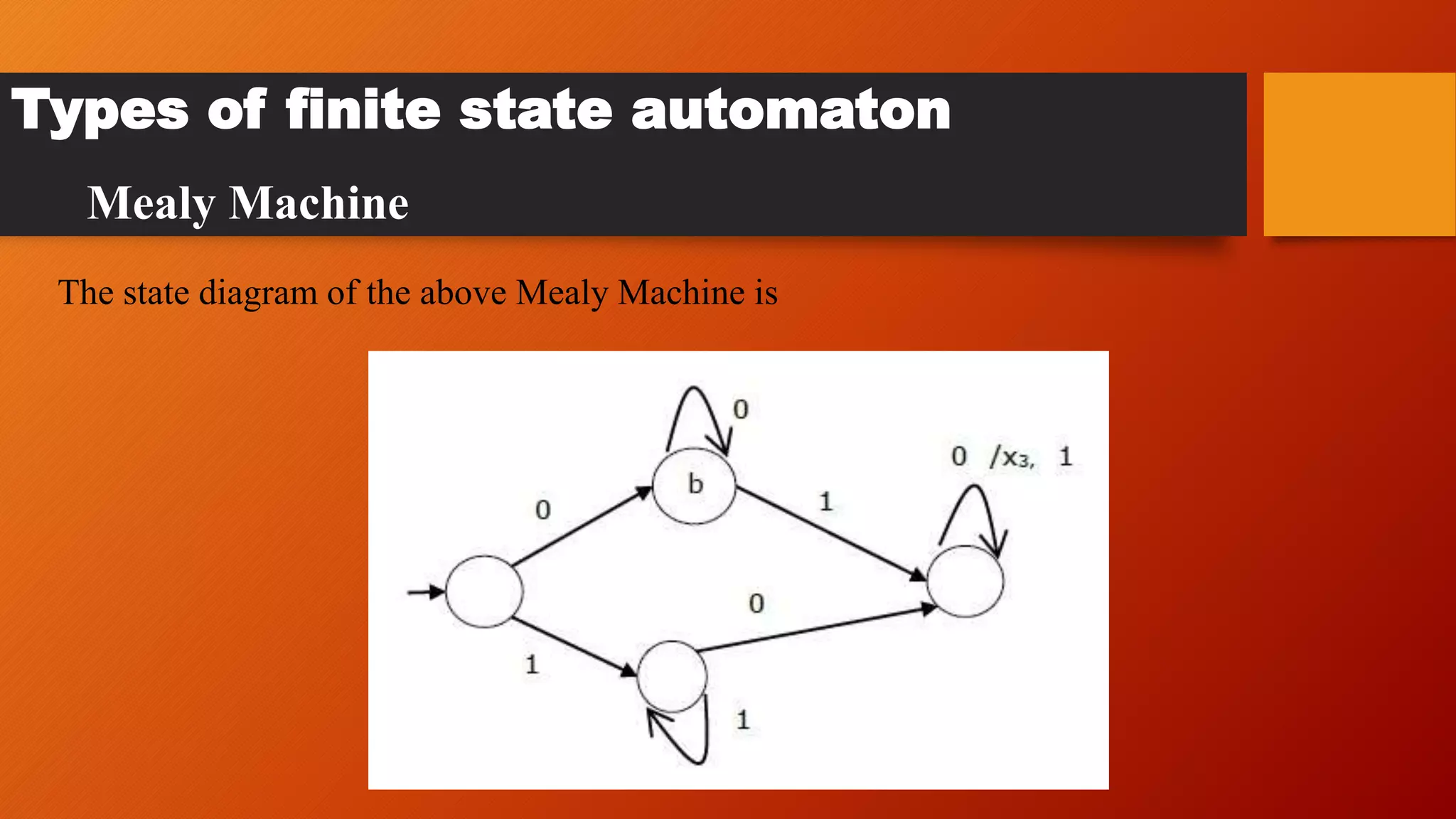
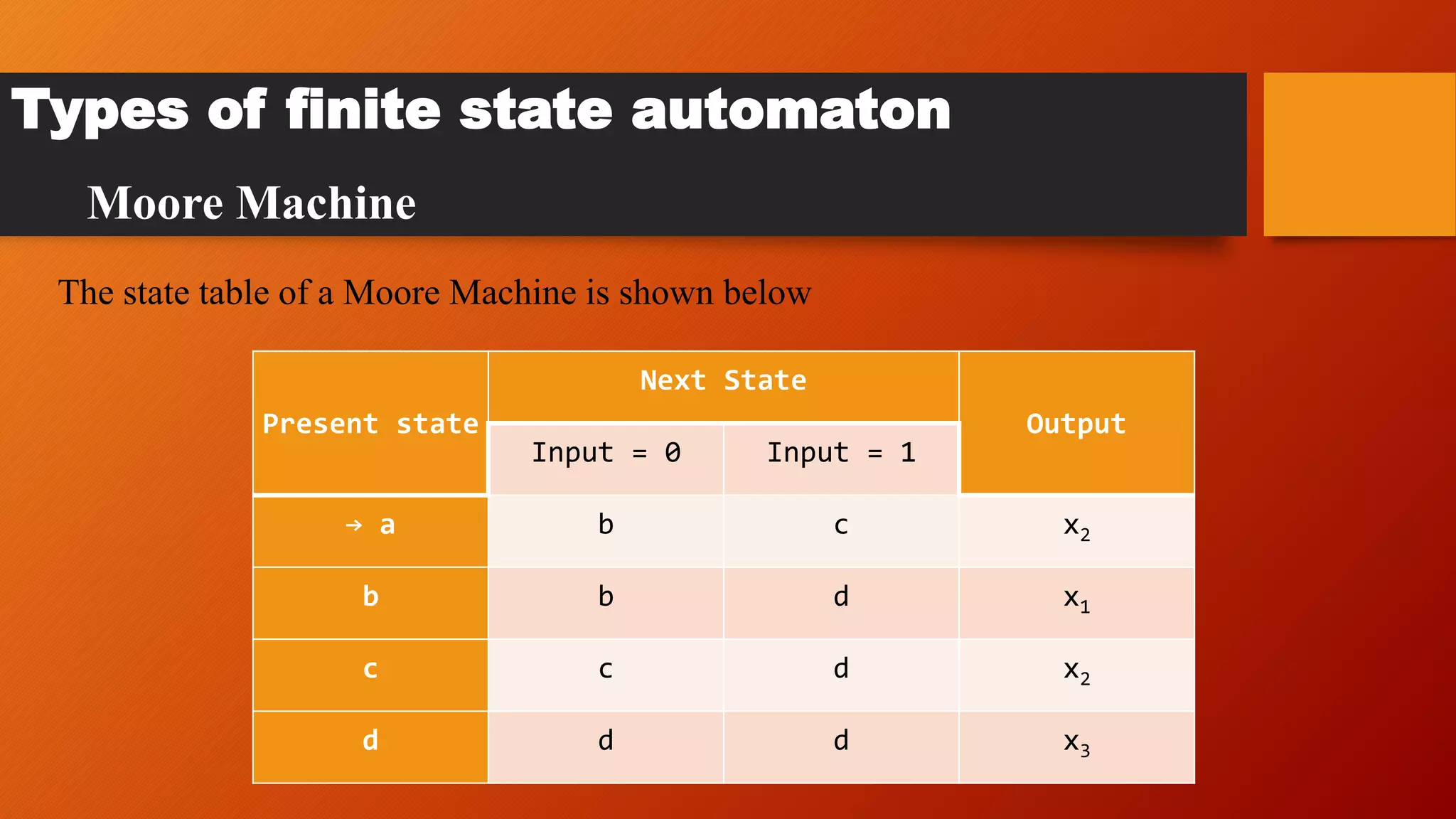
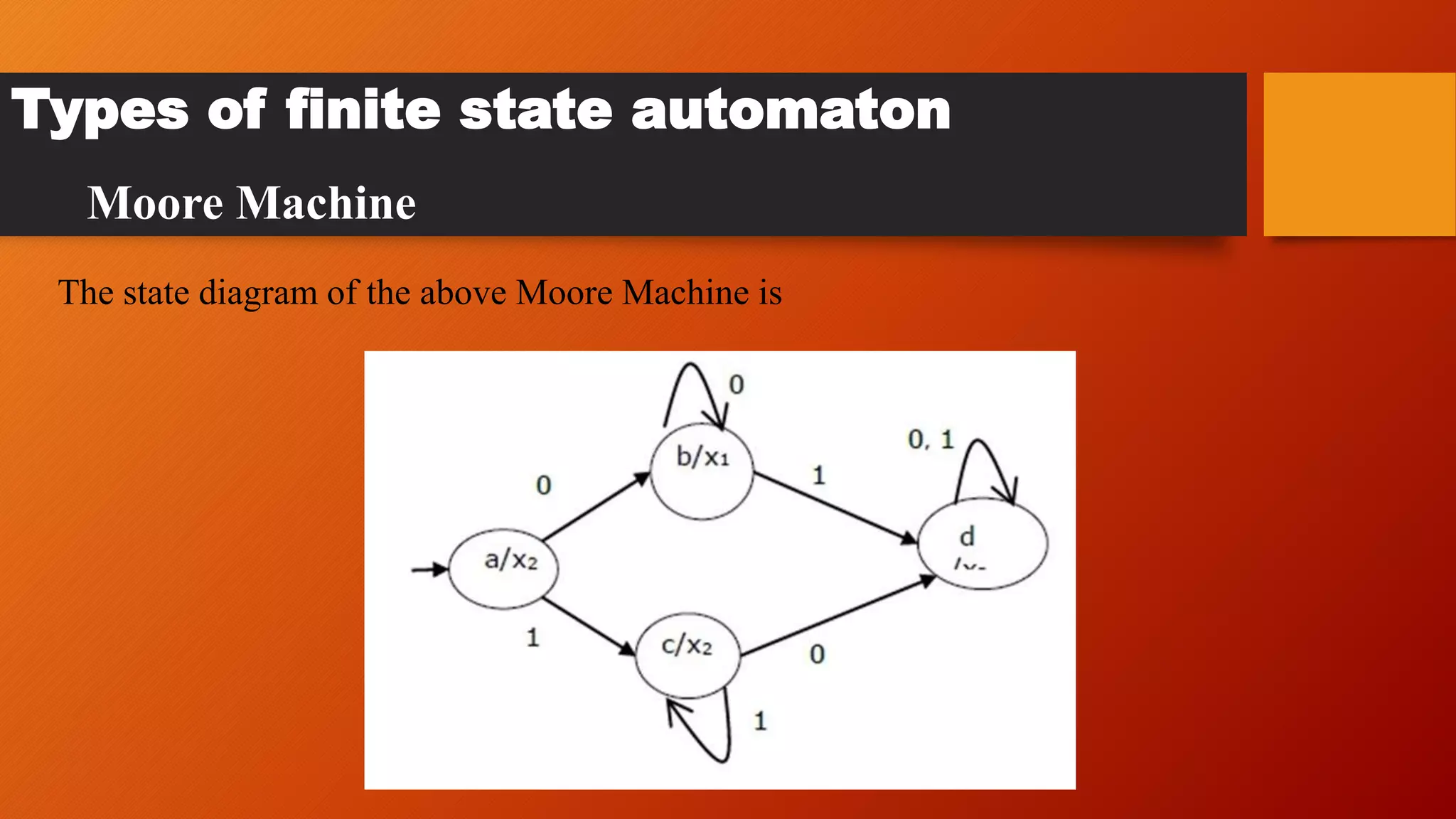
The document provides an overview of finite state automata (FSMs), including their definition, historical context, and the various types, specifically Mealy and Moore machines. It details the advantages and disadvantages of FSMs, emphasizing their simplicity, predictability, and efficiency, while also noting their limitations in managing larger systems and the rigidity in state transitions. Examples illustrate how FSMs can be applied in practical scenarios, such as elevator control systems.

1. Finite State Automaton
By:
AmmAr mobark
Second stage Software department
Babylon university
Information Technology collage
JAN. 2017

2. Index
• Introduction
• The historical of finite state automaton
• Types of finite state automaton
• The advantages and disadvantages of finite state automaton
• examples for finite state automaton

3. Introduction
Definition of finite state automaton: computation. It is an abstract
machine that can be in exactly one of a finite number of states at any given time.
The FSM can change from one state to another in response to some external
inputs; the change from one state to another is called a transition. A FSM is
defined by a list of its states, its initial state, and the conditions for each
transition.

4. Introduction
The behavior of state machines can be observed in many devices in
modern society that perform a predetermined sequence of actions depending on
a sequence of events with which they are presented. Examples are vending
machines, which dispense products when the proper combination of coins is
deposited, elevators, whose sequence of stops is determined by the floors
requested by riders, traffic lights, which change sequence when cars are waiting,
and combination locks, which require the input of combination numbers in the
proper order.

5. Introduction
The finite state machine has less computational power than some other
models of computation such as the Turing machine. The computational power
distinction means there are computational tasks that a Turing machine can do
but a FSM cannot. This is because a FSM's memory is limited by the number of
states it has. FSMs are studied in the more general field of automata theory.

6. The historical of finite state automaton
Systems which could transition between a finite number of internal
states have been known of for a long time, but it was not until relatively late in
the early history of computer science that they were formally studied.
The following quotes are from Rabin and Scott ,"Finite automata and
their decision problems "
"Turing machines are widely considered to be the abstract prototype of
digital computers; workers in the field, however, have felt more and more that
the notion of a Turing machine is too general to serve as an accurate model of
actual computers. It is well known that even for simple calculations it is
impossible to give an a priori upper bound on the amount of tape a Turing
machine will need for any given computation. It is precisely this feature that
renders Turing's concept unrealistic."

7. The historical of finite state automaton
"In the last few years the idea of a finite automaton has appeared in the
literature. These are machines having only a finite number of internal states that
can be used for memory and computation. The restriction of finiteness appears
to give a better approximation to the idea of a physical machine. Of course, such
machines cannot do as much as Turing machines, but the advantage of being
able to compute an arbitrary general recursive function is questionable, since
very few of these functions come up in practical applications."

8. Types of finite state automaton
Finite automata may have outputs corresponding to each transition. There are
two types of finite state machines that generate output
• Mealy Machine
• Moore machine

9. A Mealy Machine is an FSM whose output depends on the present state as well
as the present input.
It can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where
• Q is a finite set of states.
• ∑ is a finite set of symbols called the input alphabet.
• is a finite set of symbols called the output alphabet.
• δ is the input transition function where δ: Q × ∑ → Q
• X is the output transition function where X: Q × ∑ → O
• q0 is the initial state from where any input is processed (q0 ∈ Q).
Types of finite state automaton
Mealy Machine

10. The state table of a Mealy Machine is shown below
Types of finite state automaton
Mealy Machine
Present
state
Next state
input = 0 input = 1
State Output State Output
→ a B x1 C x1
B B x2 D x3
C D x3 C x1
D D x3 D x2

11. The state diagram of the above Mealy Machine is
Types of finite state automaton
Mealy Machine

12. Moore machine is an FSM whose outputs depend on only the present state. A
Moore machine can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where
• Q is a finite set of states.
• ∑ is a finite set of symbols called the input alphabet.
• is a finite set of symbols called the output alphabet.
• δ is the input transition function where δ: Q × ∑ → Q
• X is the output transition function where X: Q → O
• q0 is the initial state from where any input is processed (q0 ∈ Q).
Types of finite state automaton
Moore Machine

13. The state table of a Moore Machine is shown below
Types of finite state automaton
Moore Machine
Present state
Next State
Output
Input = 0 Input = 1
→ a b c x2
b b d x1
c c d x2
d d d x3

14. The state diagram of the above Moore Machine is
Types of finite state automaton
Moore Machine

15. The following table highlights the points that differentiate a Mealy Machine
from a Moore Machine.
Types of finite state automaton
Mealy Machine vs. Moore Machine
Mealy Machine Moore Machine
Output depends both upon present state and
present input.
Output depends only upon the present
state.
Generally, it has fewer states than Moore
Machine.
Generally, it has more states than Mealy
Machine.
Output changes at the clock edges. Input change can cause change in output
change as soon as logic is done.
Mealy machines react faster to inputs In Moore machines, more logic is needed to
decode the outputs since it has more
circuit delays.

16. Algorithm 4
Input − Moore Machine
Output − Mealy Machine
Step 1 − Take a blank Mealy Machine transition table format.
Step 2 − Copy all the Moore Machine transition states into this table format.
Step 3 − Check the present states and their corresponding outputs in the Moore
Machine state table; if for a state Qi output is m, copy it into the output columns
of the Mealy Machine state table wherever Qi appears in the next state.
Types of finite state automaton
Moore Machine to Mealy Machine

17. Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are
available in the state table of the Mealy machine.
Step 2 − If all the outputs of Qi are same, copy state Qi. If it has n distinct
outputs, break Qi into n states as Qin where n = 0, 1, 2.......
Step 3 − If the output of the initial state is 1, insert a new initial state at the
beginning which gives 0 output.
Types of finite state automaton
Mealy Machine to Moore Machine

18. The advantages and disadvantages
• Their simplicity make it easy for inexperienced developers to implement with
little to no extra knowledge (low entry level)
• Predictability (in deterministic FSM), given a set of inputs and a known
current state, the state transition can be predicted, allowing for easy testing
• Due to their simplicity, FSMs are quick to design, quick to implement and
quick in execution
• FSM is an old knowledge representation and system modeling technique, and
its been around for a long time, as such it is well proven even as an artificial
intelligence technique, with lots of examples to learn from
Advantages of FSM

19. The advantages and disadvantages
• FSMs are relatively flexible. There are a number of ways to implement a FSM
based system in terms of topology, and it is easy to incorporate many other
techniques
• Easy to transfer from a meaningful abstract representation to a coded
implementation
• Low processor overhead; well suited to domains where execution time is
shared between modules or subsystems. Only the code for the current state
need be executed, and perhaps a small amount of logic to determine the
current state.
• Easy determination of reachability of a state, when represented in an abstract
form, it is immediately obvious whether a state is achievable from another
state, and what is required to achieve the state
Advantages of FSM

20. The advantages and disadvantages
• The predictable nature of deterministic FSMs can be unwanted in some
domains such as computer games (solution may be non-deterministic FSM).
• Larger systems implemented using a FSM can be difficult to manage and
maintain without a well thought out design. The state transitions can cause a
fair degree of "spaghetti- factor" when trying to follow the line of execution
• Not suited to all problem domains, should only be used when a systems
behavior can be decomposed into separate states with well defined conditions
for state transitions. This means that all states, transitions and conditions need
to be known up front and be well defined
• The conditions for state transitions are ridged, meaning they are fixed (this can
be over come by using a Fuzzy State Machine (FuSM))
Disadvantages of FSM

21. examples of finite state automaton
Step 1: Describe the machine in words.
In this example, we’ll be designing a controller for an elevator. The
elevator can be at one of two floors: Ground or First. There is one button that
controls the elevator, and it has two values: Up or Down. Also, there are two
lights in the elevator that indicate the current floor: Red for Ground, and Green
for First. At each time step, the controller checks the current floor and current
input, changes floors and lights in the obvious way.

22. examples of finite state automaton
Step 2: Draw the FSM diagram
In this diagram, the bubbles
represent the states, and the arrows
represent state transitions. The arrow
labels indicate the input value
corresponding to the transition. For
instance, when the elevator is in the
Ground state, and the input is Up,
the next state is First. The
information in the brackets indicates
the output values for the lights in
each state.

23. examples of finite state automaton
Step 3: Select numbers to represent states and values
Before converting the above FSM diagram to a circuit, we need to
represent every value in our example as a binary number. Here is some
convenient numbers to use.
Ground = 0 Down = 0 Off = 0
First = 1 up = 1 no = 1

24. examples of finite state automaton
Step 4: Write the truth table
From the FSM diagram, it is easy to read off the correct truth table
greenredNext stateinputCurrent state
01000
01110
10001
10111