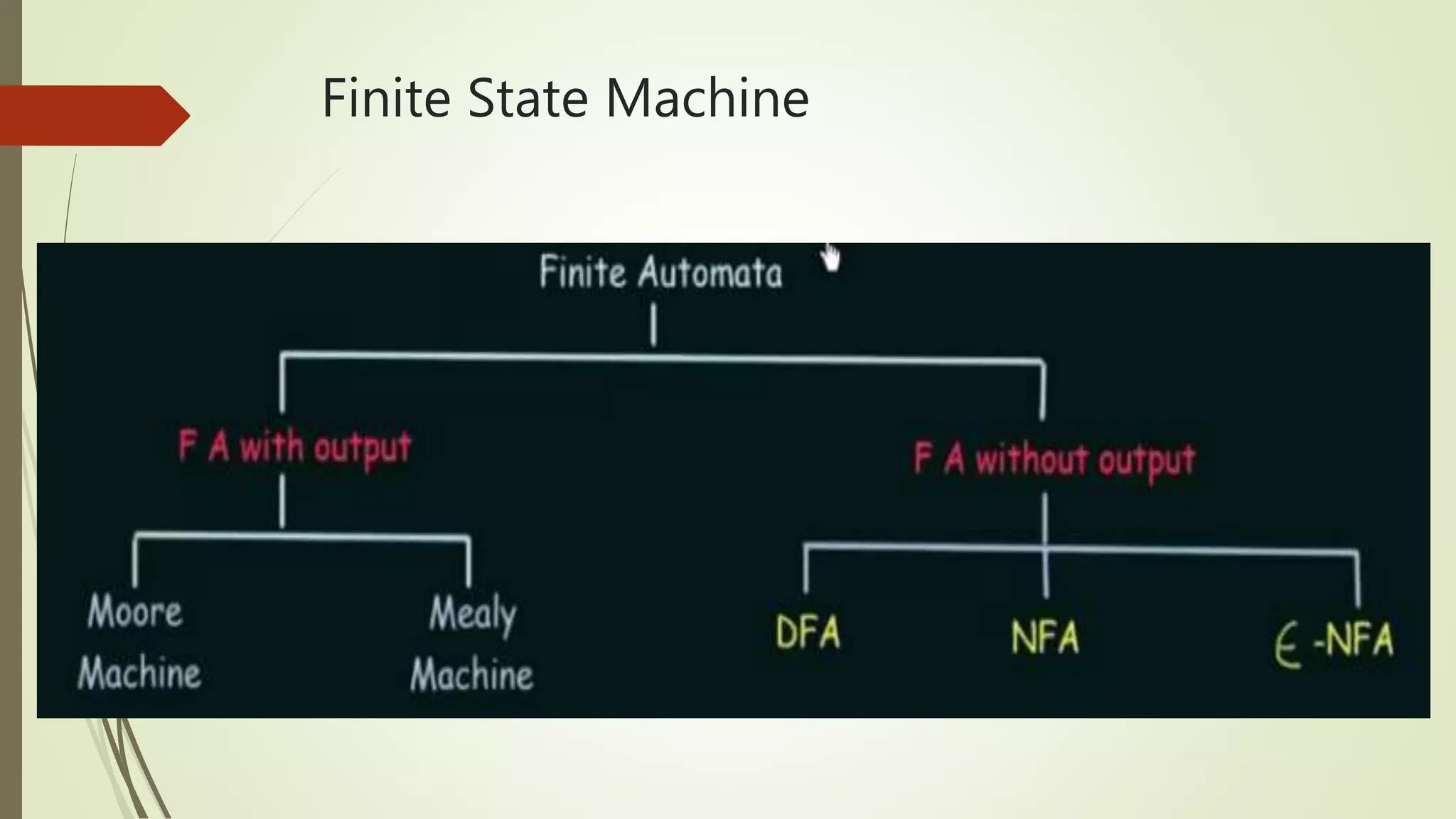
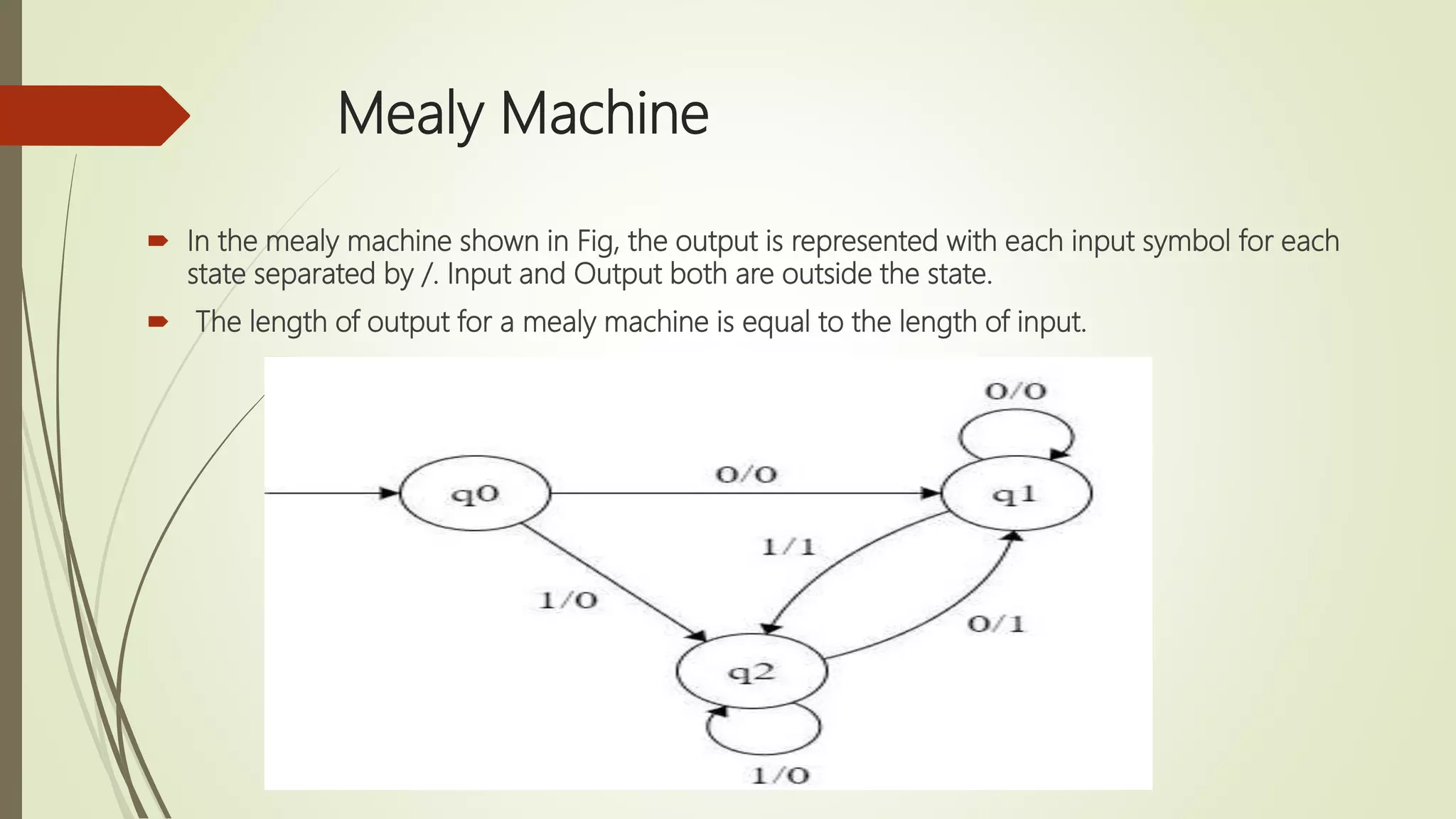
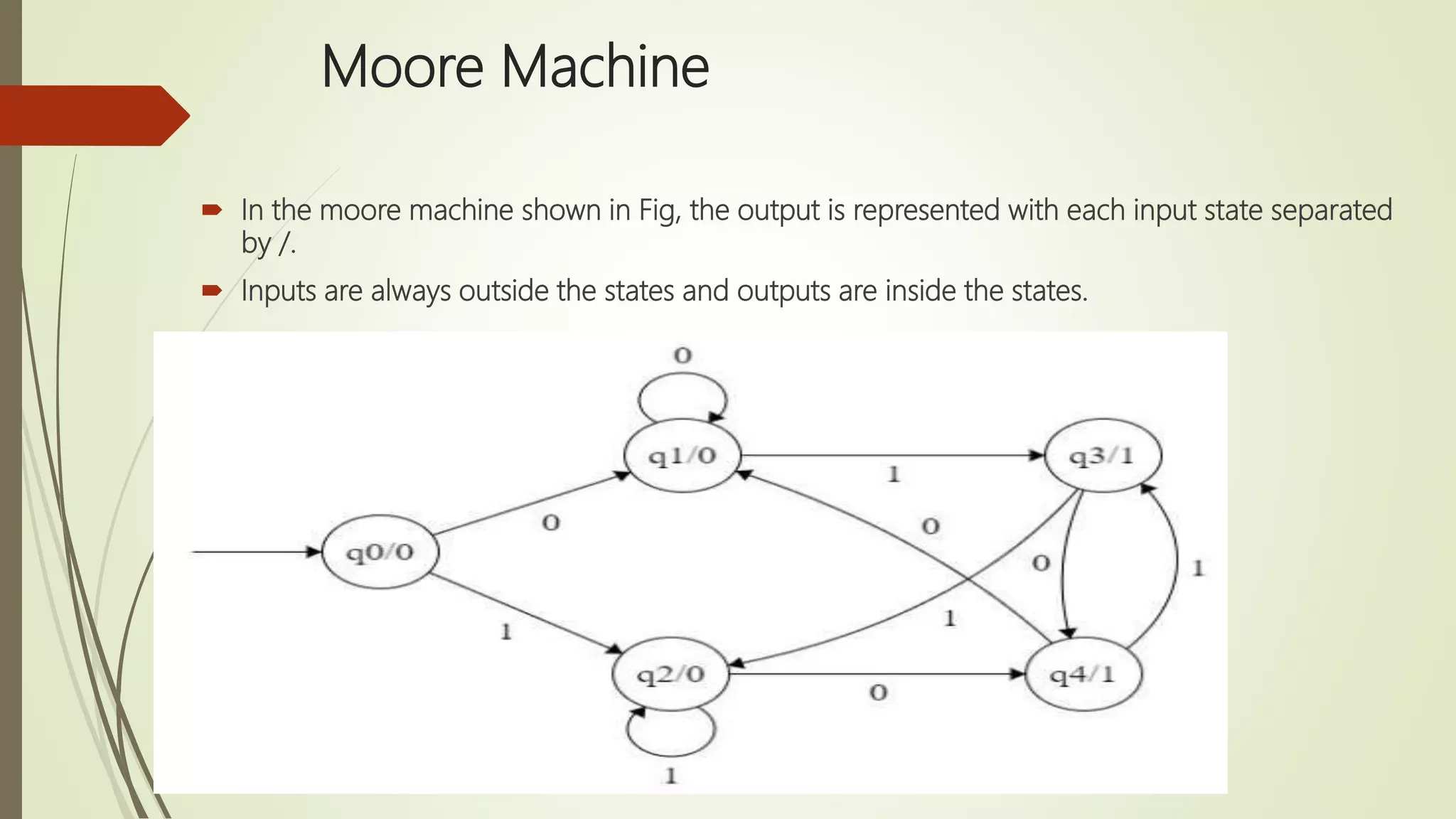
Moore and Mealy machines are two types of finite state machines. A Mealy machine's output depends on the current state and input, and its output size equals its input size. A Moore machine's output depends only on the current state, and its output size is one larger than its input size. Mealy machines are defined as tuples including states, inputs, outputs, transitions, and an output function. Moore machines are similarly defined except the output function maps states to outputs rather than states and inputs. Examples of Moore and Mealy machine applications include elevators, compilers, SRAM, and vending machines.

1. Moore and Mealy Machines

2. What is Finite Automata???
Finite Automata(FA) is the simplest machine to recognize
patterns.
A Finite Automata consists of the following :
Q : Finite nonempty set of states.
∑ : set of finite nonempty Input Symbols.
q : Initial state.
F : set of (Multiple) Final States.
δ : Transition Function which maps Q×∑ → Q.

3. The formal specification of machine is
(Q ∑ q F δ)
5 tuples

4. Finite State Machine

5. Need To understand about Moore and
Mealy
 Both machines must have Initial state but final state is not
mandatory.

6. Mealy Machine
 Mealy machines are also finite state machines with output value and its output depe
nds on present state and current input symbol.
 t can be defined as (Q, q0, ∑, O, δ, λ’) where:
 Q is finite set of states.
 q0 is the initial state.
 ∑ is the input alphabet.
 O is the output alphabet.
 δ is transition function which maps Q×∑ → Q.
 ‘λ’ is the output function which maps Q×∑→ O.

7. Mealy Machine
 In the mealy machine shown in Fig, the output is represented with each input symbol for each
state separated by /. Input and Output both are outside the state.
 The length of output for a mealy machine is equal to the length of input.

8. Mealy Machine
 Input: 11
 Output: 00 (q0 to q2 transition has Output 0 and q2 to q2 transition also
has Output 0)
 So,
size of Input= Size of Output
N=N

9. Moore Machine
 Moore machines are finite state machines with output value and its output depends only on
present state . For every state output is associated.
 It can be defined as (Q, q0, ∑, O, δ, λ) where:
 Q is finite set of states.
 q0 is the initial state.
 ∑ is the input alphabet.
 O is the output alphabet.
 δ is transition function which maps Q×∑ → Q.
 λ is the output function which maps Q → O.

10. Moore Machine
 In the moore machine shown in Fig, the output is represented with each input state separated
by /.
 Inputs are always outside the states and outputs are inside the states.

11. Moore Machine
 The length of output for a moore machine is greater than input by 1.
 Input: 11
 Output: 000 (0 for q0, 0 for q2 and again 0 for q2)
 so.,
Size of input ≠ Size of Output
N=N+1

12. Construct Mealy machine from the given
table

13. Construct a Moore Machine
from the given table

14. Practical Applications of moore and mealy
machines
 implementation of Elevator functionality
 The lexical analysis part of your compiler/interpreter (yes, even your shell) is
again a finite automaton which matches keywords and other tokens recognized by
the language.
 Moore machine is used in SRAM because of its speed.
 Any vending machine is a finite automaton which takes in coins of different
denominations and recognizes when the correct amount has been entered (OK,
today's vending machines probably have a small CPU inside doing the adding, but
the end result is the same).