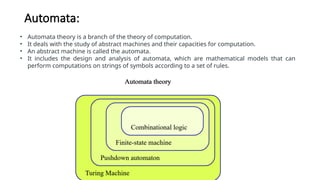
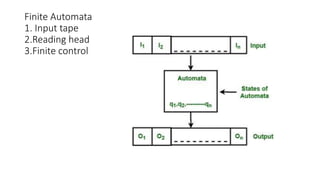
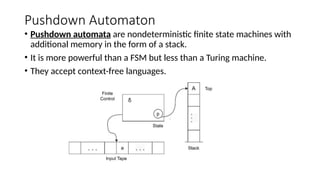
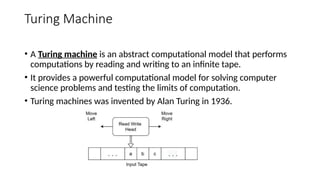
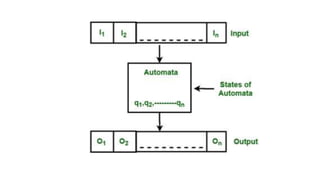
A finite-state machine (FSM) is a mathematical model that can exist in one of a finite number of states and change states based on inputs, defined by its states, initial state, and transition inputs. Automata theory studies abstract machines, including FSMs and more powerful models like pushdown automata, which utilize stacks for additional memory, and Turing machines, which can perform computations with an infinite tape. Finite automata are the simplest form of these machines, capable of recognizing patterns based on their defined states and transitions.

1. Finite State Machine

2. FSM
• A finite-state machine (FSM) or finite-state automaton (FSA,
plural: automata), finite automaton, or simply a state machine, is a
mathematical model of computation.
• It is an abstract machine that can be in exactly one of a finite number
of states at any given time.
• The FSM can change from one state to another in response to
some inputs; the change from one state to another is called
a transition.
• An FSM is defined by a list of its states, its initial state, and the inputs
that trigger each transition.

3. FSM
• A finite state machine consists of
• Input tape: Divided in to number of cells , which contains single input
symbol
• 2. Reading head: Read only one cell at a time and move only in one
direction and
• 3. Finite control: Act like CPU. Depending on the current state and
input symbol read from the state. Finite state machine have no
memory

4. Automata:
• Automata theory is a branch of the theory of computation.
• It deals with the study of abstract machines and their capacities for computation.
• An abstract machine is called the automata.
• It includes the design and analysis of automata, which are mathematical models that can
perform computations on strings of symbols according to a set of rules.

5. Finite Automata
1. Input tape
2.Reading head
3.Finite control

6. Types of computational models
• A finite-state machine (FSM) is a mathematical model of computation
that can be in one of a finite number of states at any given time.
• It can change from one state to another in response to inputs, called
a transition.

7. Pushdown Automaton
• Pushdown automata are nondeterministic finite state machines with
additional memory in the form of a stack.
• It is more powerful than a FSM but less than a Turing machine.
• They accept context-free languages.

8. Contd..
• For example, to ensure a valid code, a programmer can feed the code
into a pushdown automaton programmed with transition functions
that implement the context-free grammar for the language of
balanced parentheses.
• If the code is valid and all parentheses are matched, the pushdown
automaton will accept the code.
• If unbalanced parentheses are present, the automaton can return the
code's invalidity.

9. Turing Machine
• A Turing machine is an abstract computational model that performs
computations by reading and writing to an infinite tape.
• It provides a powerful computational model for solving computer
science problems and testing the limits of computation.
• Turing machines was invented by Alan Turing in 1936.

10. Contd..
• A Turing Machine consists of an infinite tape, a tape head, and a state
transition table.
• They execute on an input string of bits, with the tape head in a certain
state and the table governing its behavior.
• Turing machines can simulate the complexity of a program and its
reactions to different data in memory.

11. Finite Automata
• Finite Automata (FA) is the simplest machine to recognize patterns
(Regular Expression).
• The finite automata or finite state machine is an abstract machine
which has five elements or tuple.
• It has a set of states and rules for moving from one state to another
but it depends upon the applied input symbol.
• Basically it is an abstract model of digital computer.

13. Contd..
Features of automata:
• Input
• Output
• States of automata
• State relation
• Output relation

14. Contd..
• A Finite Automata consists of the following :
M= { Q, Σ, q0, F, δ }
Q : Finite set of states.
Σ : set of Input Symbols.
q0 : Initial state.
F : set of Final States.
δ : Transition Function