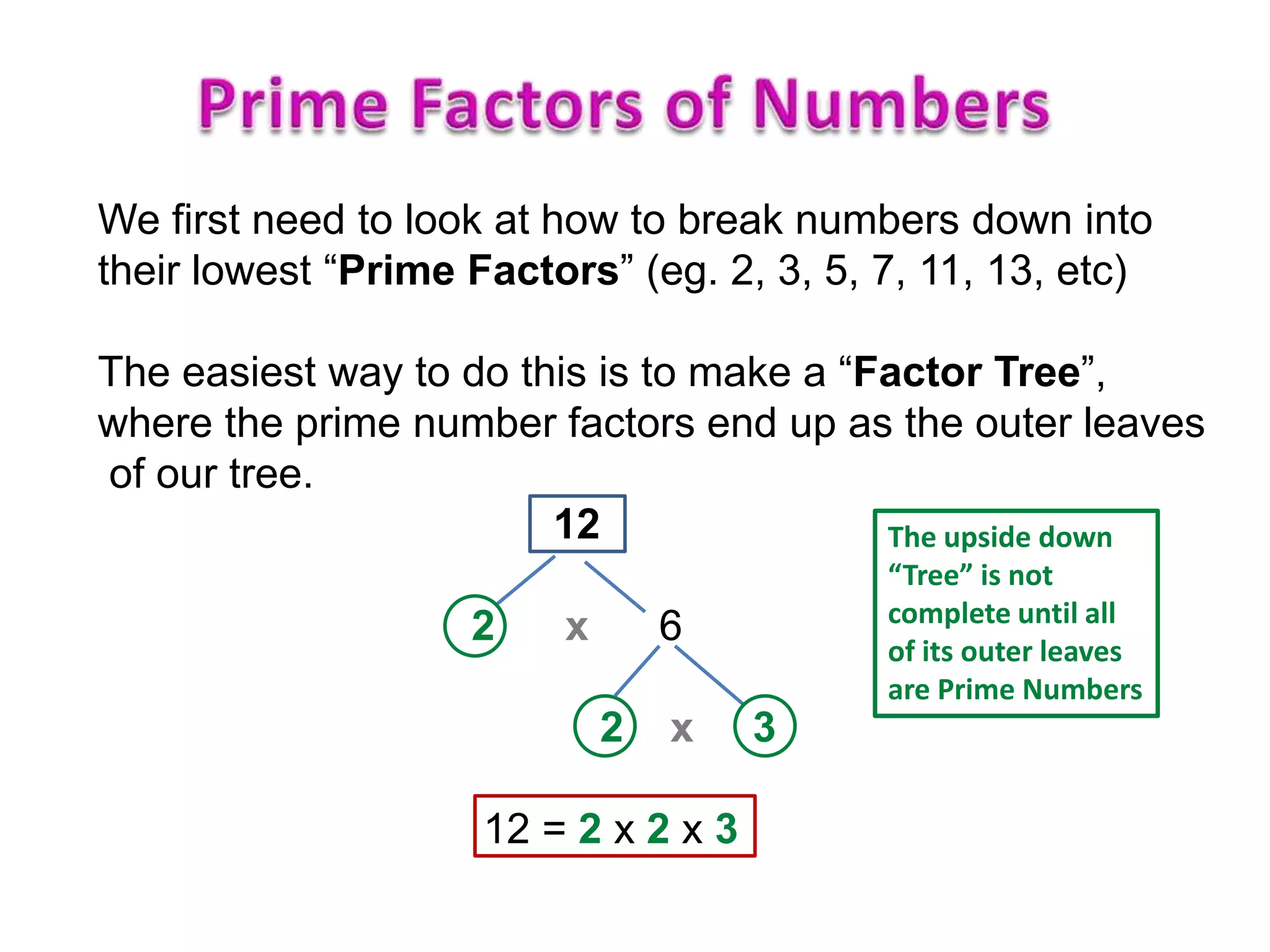
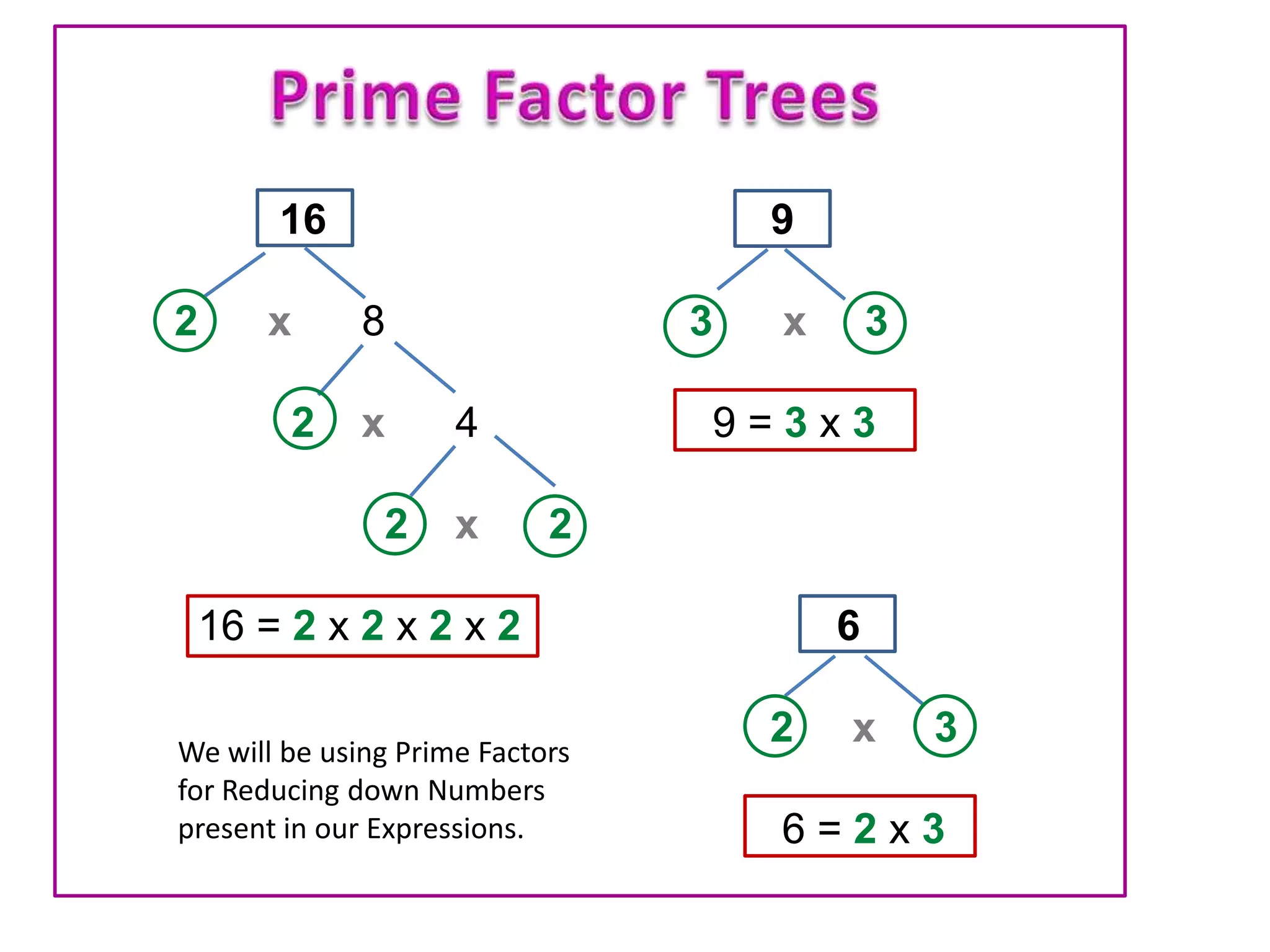
This document discusses finding the common factor of algebraic expressions. It explains that to find the common factor, one must break down all numbers within the expressions into their prime number factors. The common factors that are present in both expressions are then written outside of parentheses, while the remaining terms are written inside. Several examples are provided of factorizing expressions using this process of identifying common prime factors. The "highest common factor" refers to the largest common factor present outside of the parentheses.

1. What do these Two Groups have in Common ?

2. Passy is in both Groups !
To find the “Common Factor” we need to break down the group
into its smallest possible components, and then see which of these
components is the same, or “common” to both groups.
For mathematical numbers and Algebra Terms, we find the
“Common Factor” by breaking down the number part into a set
of “Prime Numbers”, and seeing which of these Prime Numbers
is “common” to both of our starting items.

3. We first need to look at how to break numbers down into
their lowest “Prime Factors” (eg. 2, 3, 5, 7, 11, 13, etc)
The easiest way to do this is to make a “Factor Tree”,
where the prime number factors end up as the outer leaves
of our tree.
12
2 x 6
2 x 3
12 = 2 x 2 x 3
The upside down
“Tree” is not
complete until all
of its outer leaves
are Prime Numbers

4. 16 9
2 x 8 3 x 3
2 x 4 9 = 3 x 3
2 x 2
16 = 2 x 2 x 2 x 2 6
2 x 3
6 = 2 x 3
We will be using Prime Factors
for Reducing down Numbers
present in our Expressions.

5. 2 (a + 6) = 2a + 12
To create “Factor Form” we work backwards
by breaking down and Factorising an expanded
answer back into its original brackets form.
“Expanded Form” looks like this:
2a + 12 = 2(a + 6)

6. To Factorise into Brackets Form, follow these steps:
 Break Numbers into their Lowest Prime Factors
 Expand out fully all Powers Exponents Terms
 Identify the “Common Factors”
 Write the Factor Form as:
Common Factors ( Left Over Items )
 Put Final Answer into simplest form, whole numbers etc

7. 6
6m + 9 Write Numbers as Prime Factors
(Use Factor Trees to help you)
6
2 x 3
6 = 2 x 3
9
3 x 3
9 = 3 x 3
6m + 9 = 2 x 3 x m + 3 x 3
= 2 x 3 x m + 3 x 3
Now Circle once what is in Common in the two groups
Put Common Factor outside a set of brackets once,
and put all the “leftovers” inside the brackets.
= 3 ( 2 x m + 3)
= 3(2m + 3)

8. 6
4w - 2 Write Numbers as Prime Factors
(Use Factor Trees to help you)
4
2 x 2
4 = 2 x 2
2
2 x 1
2 = 2 x 1
4w - 2 = 2 x 2 x w - 2 x 1
= 2 x 2 x w - 2 x 1
Now Circle what is in Common in the two groups
Put Common Factor outside a set of brackets once,
and put all the “leftovers” inside the brackets.
= 2 ( 2 x w - 1)
= 2(2w - 1)

9. N
Factorise 12ab + 16bv
12ab + 16bv = 2x2x3xaxb + 2x2x2x2xbxv
= 2x2x3xaxb + 2x2x2x2xbxv
2 x 2 x b is the Common Factor in the two groups
= 2 x 2 x b ( 3xa + 2x2xv )
= 4b(3a + 4v)
Note that the “4b” outside the Brackets is called the “Highest Common Factor”

10. Factorise 12a2
c3
- 9ab2
= 2x2x3 x a x a x c x c x c - 3x3 x a x b x b
= 2x2x3 x a x a x c x c x c - 3x3 x a x b x b
= 3 x a ( 2 x 2 x a x c x c x c - 3 x b x b )
= 3a(4ac3
- 3b2
)

11. 6
Factorise 8a2
b2
+ 16abc
= 2x2x2 x axa x bxb + 2x2x2x2 x a x b x c
= 2x2x2 x axa x bxb + 2x2x2x2 x a x b x c
= 2x2x2 x a x b ( a x b + 2 x c )
= 8ab(ab + 2c)
Note that the “8ab” outside the Brackets is called the “Highest Common Factor”

12. Factorise - 3eh + - 8ehk
= 3 x -1 x e x h + 8 x -1 x e x h x k
= 3 x -1 x e x h + 8 x -1 x e x h x k
= -1 x e x h (3 + 8k)
= -eh(3 + 8k)
Note that the “-eh” outside the Brackets is called the “Highest Common Factor”

13. http://passyworldofmathematics.com
Visit our Site for Free Mathematics PowerPoints