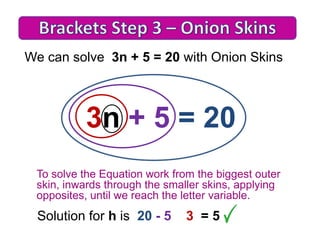
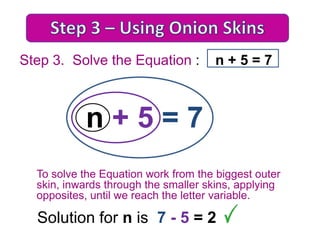
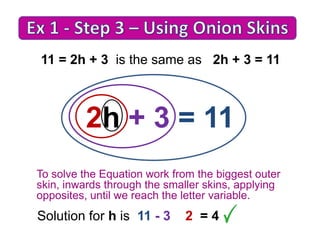
This document provides steps for solving equations with variables on both sides: 1. Expand any brackets first. 2. Identify the smaller term with the variable. 3. Apply the opposite operation (+ or -) to that term on both sides. 4. Simplify and solve the resulting equation normally using techniques like onion skins or backtracking. Worked examples demonstrate subtracting and adding the smaller variable term to move it to one side.

1. Image Source: http://oliveloafdesign.wordpress.com

2. Solve the Equation :
3n + 5 = 2n + 7
We cannot solve this Equation using “Onion
Skins” or “Back-Tracking”, because our
Variable letter “n” is on both
sides of the Equation. 
WE NEED TO DO SOME EXTRA STEPS
BEFORE WE CAN SOLVE THE EQUATION

3. Solve the Equation :
3n + 5 = 2n + 7
The Extra Steps are:
1. Identify the smaller letter term.
2. Apply the Opposite Operation ( + or - ) to
this smaller item on both sides.
3. Simplify and Solve the Equation as normal.

4. 3n + 5 = 2n + 7
Step 1. Identify the smaller letter term.
3n + 5 = 2n + 7
Step 2. SUBTRACT it from both sides
3n + 5 = 2n + 7
-2n
-2n
n+5=
7
Step 3. Solve as normal (See next slide)

5. Step 3. Solve the Equation :
n+5=7
n+5=7
To solve the Equation work from the biggest outer
skin, inwards through the smaller skins, applying
opposites, until we reach the letter variable.
Solution for n is 7 - 5 = 2

6. 11 – 5h = 3h + 3
-
Step 1. Identify the smaller letter term.
11 – 5h = 3h + 3
-
Step 2. ADD it to both sides
11 – 5h = 3h + 3
+5h +5h
11
= 2h + 3
-
Step 3. Solve as normal (See next slide)

7. 11 = 2h + 3 is the same as 2h + 3 = 11
2h + 3 = 11
To solve the Equation work from the biggest outer
skin, inwards through the smaller skins, applying
opposites, until we reach the letter variable.
Solution for h is 11 - 3
2 =4

8. Solve :
5(n + 1) = 2(n + 20)
We cannot solve this Equation using “Onion
Skins” or “Back-Tracking”, because our
Brackets and the Variable letter “n”
are on both sides of the Equation.
WE NEED TO EXPAND THE BRACKETS
BEFORE WE CAN SOLVE THE EQUATION

9. 5(n + 1) = 2(n + 10)
5(n + 1) = 2(n + 10)
5n + 5 = 2n + 20
Now Solve a Letters Both Sides Equation
5n + 5 = 2n + 20
-2n
-2n
3n + 5 =
20
Step 3. Solve as normal (See next slide)

10. We can solve 3n + 5 = 20 with Onion Skins
3n + 5 = 20
To solve the Equation work from the biggest outer
skin, inwards through the smaller skins, applying
opposites, until we reach the letter variable.
Solution for h is 20 - 5
3 =5

11. Working Out Steps are:
1. Expand any Brackets First
2. Identify the smaller letter term.
3. Apply the Opposite Operation ( + or - ) to
this smaller item on both sides.
4. Simplify and Solve the Equation as normal*.
(* Use Onion Skins, Algebra Reversing,
or Backtracking with Flowcharts )

12. http://passyworldofmathematics.com/
All Images and Diagrams are Copyright by Passy’s World of Mathematics