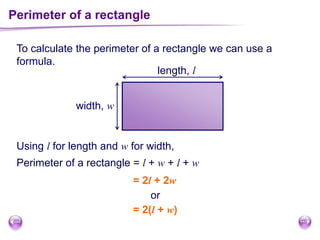
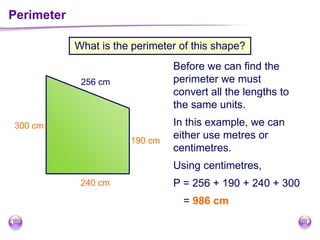
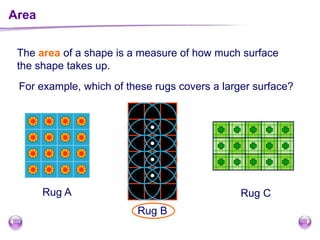
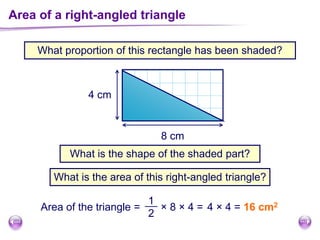
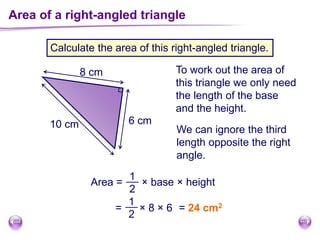
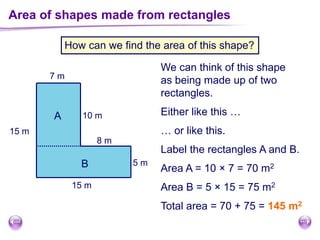
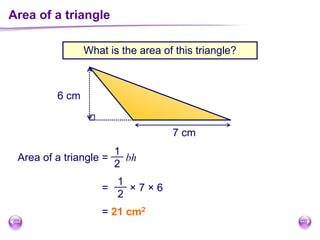
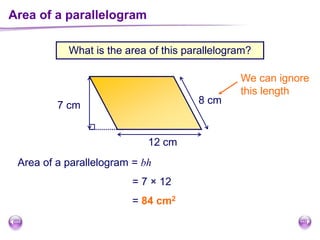
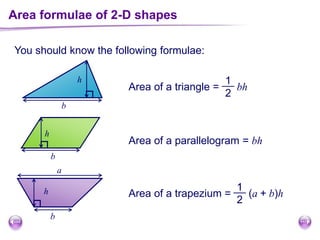
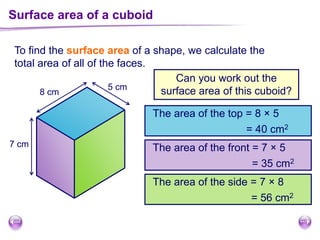
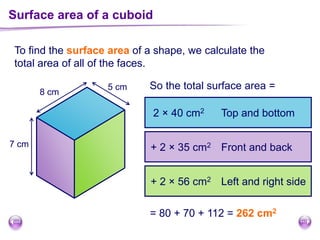
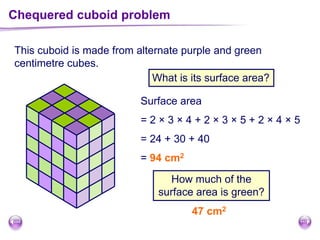
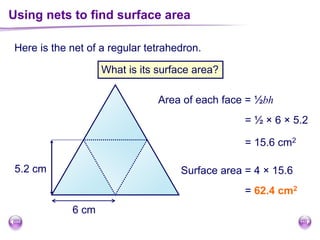
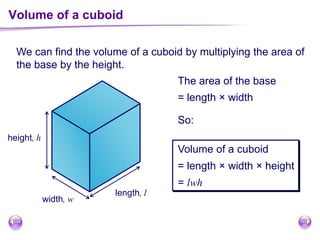
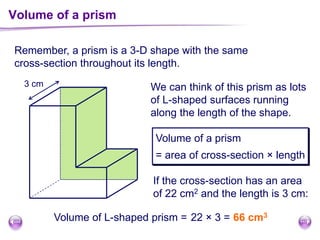
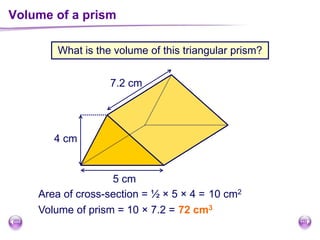
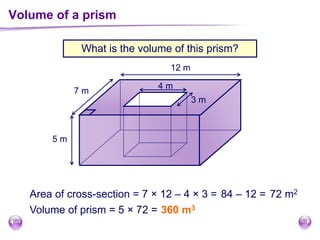
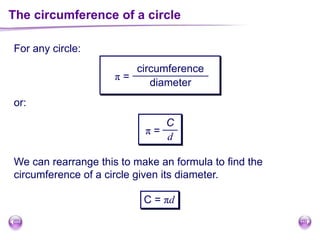
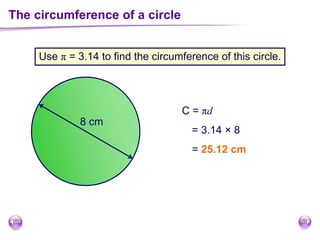
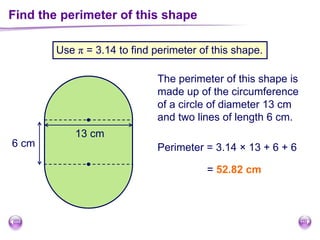
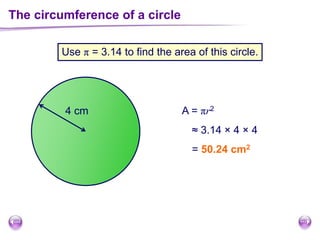
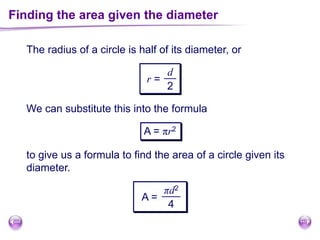
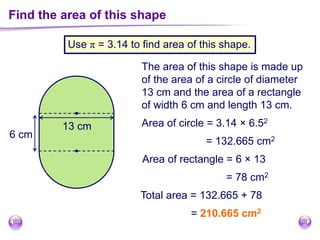
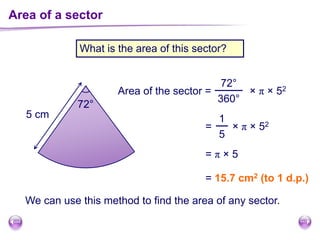
This document discusses perimeter, area, and volume. It begins by defining perimeter as the distance around a shape found by adding all the side lengths. It provides examples of calculating perimeters of rectangles, irregular shapes, and converting between units. It then defines area as a measure of how much surface a shape covers. It gives formulas and examples for finding the areas of rectangles, triangles, parallelograms, trapezoids, and irregular shapes. Finally, it discusses surface area as the total area of all faces of a shape. It provides the surface area formulas and worked examples for cuboids and cubes.

1. Perimeter, area and
volume

2. A
A
A
A
A
A
Contents
S8 Perimeter, area and volume
S8.1 Perimeter
S8.6 Area of a circle
S8.2 Area
S8.5 Circumference of a circle
S8.3 Surface area
S8.4 Volume

3. Put these shapes in order

4. Perimeter
To find the perimeter of a shape we add together the
length of all the sides.
What is the perimeter of this shape?
1 cm
3
3
2
1
1
2
Perimeter = 3 + 3 + 2 + 1 + 1 + 2
= 12 cm
Starting point

5. Perimeter of a rectangle
To calculate the perimeter of a rectangle we can use a
formula.
length, l
width, w
Using l for length and w for width,
Perimeter of a rectangle = l + w + l + w
= 2l + 2w
or
= 2(l + w)

6. Perimeter
What is the perimeter of
this shape?
b cm
a cm
9 cm
5 cm
12 cm 4 cm
The lengths of two of
the sides are not given
so we have to work
them out before we can
find the perimeter.
Let’s call the lengths a and b.
Sometimes we are not given the lengths of all the sides.
We have to work them out using the information we are
given.

7. Perimeter
9 cm
5 cm
b cm
12 cm
a cm
4 cm
a = 12 – 5 cm
= 7 cm
7 cm
b = 9 – 4 cm
= 5 cm
5 cm
P = 9 + 5 + 4 + 7 + 5 + 12
= 42 cm
Sometime we are not given the lengths of all the sides.
We have to work them out from the information we are
given.

8. Calculate the lengths of the missing
sides to find the perimeter.
P = 5 + 2 + 1.5 + 6 + 4
+ 2 + 10 + 2 + 4 + 6
+ 1.5 + 2
Perimeter
5 cm
2 cm
6 cm
4 cm4 cm
2 cm
2 cm
p
q r
s
t
u
p = 2 cm
q = r = 1.5 cm
s = 6 cm
t = 2 cm
u =10 cm
= 46 cm

9. P = 5 + 4 + 4 + 5 + 4 + 4
Perimeter
What is the perimeter of this shape?
Remember, the dashes
indicate the sides that are
the same length.
5 cm
4 cm
= 26 cm

10. Perimeter
Perimeter = 4.5 + 2 + 1 + 2
+ 1 + 2 + 4.5
Start by finding the lengths
of all the sides.
5 m
2 m
2 m
2 m
4 m
4.5 m 4.5 m
1 m1 m
= 17 m
What is the perimeter of this shape?

11. Before we can find the
perimeter we must
convert all the lengths to
the same units.
Perimeter
3 m
2.4 m
1.9 m
256 cm
In this example, we can
either use metres or
centimetres.
Using centimetres,
300 cm
240 cm
190 cm
P = 256 + 190 + 240 + 300
= 986 cm
What is the perimeter of this shape?

12. Equal perimeters
Which shape has a different
perimeter from the first shape?
A B C
A B C
A B C
B
A
A

13. Contents
S8 Perimeter, area and volume
A
A
A
A
A
A
S8.2 Area
S8.1 Perimeter
S8.6 Area of a circle
S8.5 Circumference of a circle
S8.3 Surface area
S8.4 Volume

14. The area of a shape is a measure of how much surface
the shape takes up.
Area
For example, which of these rugs covers a larger surface?
Rug A
Rug B
Rug C

15. Area of a rectangle
Area is measured in square units.
We can use mm2, cm2, m2 or km2.
The 2 tells us that there are two dimensions, length and width.
We can find the area of a rectangle by multiplying the length
and the width of the rectangle together.
length, l
width, w
Area of a rectangle
= length × width
= lw

16. Area of a rectangle
What is the area of this rectangle?
8 cm
4 cm
Area of a rectangle = lw
= 8 cm × 4 cm
= 32 cm2

17. Area of a right-angled triangle
What proportion of this rectangle has been shaded?
8 cm
4 cm
What is the shape of the shaded part?
What is the area of this right-angled triangle?
Area of the triangle = × 8 × 4 =
1
2
4 × 4 = 16 cm2

18. We can use a formula to find the area of a right-angled
triangle:
Area of a right-angled triangle
base, b
height, h
Area of a triangle =
1
2
× base × height
=
1
2
bh

19. Area of a right-angled triangle
Calculate the area of this right-angled triangle.
6 cm
8 cm
10 cm
To work out the area of
this triangle we only need
the length of the base
and the height.
We can ignore the third
length opposite the right
angle.
Area =
1
2
× base × height
= × 8 × 6
1
2
= 24 cm2

20. Area of shapes made from rectangles
How can we find the area of this shape?
7 m
10 m
8 m
5 m
15 m
15 m
We can think of this shape
as being made up of two
rectangles.
Either like this …
… or like this.
Label the rectangles A and B.
A
B Area A = 10 × 7 = 70 m2
Area B = 5 × 15 = 75 m2
Total area = 70 + 75 = 145 m2

21. Area of shapes made from rectangles
How can we find the area of the shaded shape?
We can think of this shape
as being made up of one
rectangle with another
rectangle cut out of it.
7 cm
8 cm
3 cm
4 cm Label the rectangles A and B.
A
B
Area A = 7 × 8 = 56 cm2
Area B = 3 × 4 = 12 cm2
Total area = 56 – 12 = 44 cm2

22. ED
C
B
A
Area of an irregular shapes on a pegboard
We can divide the shape into
right-angled triangles and a
square.
Area A = ½ × 2 × 3 = 3 units2
Area B = ½ × 2 × 4 = 4 units2
Area C = ½ × 1 × 3 = 1.5 units2
Area D = ½ × 1 × 2 = 1 unit2
Area E = 1 unit2
Total shaded area = 10.5 units2
How can we find the area of this irregular
quadrilateral constructed on a pegboard?

23. C D
BA
Area of an irregular shapes on a pegboard
An alternative method would
be to construct a rectangle
that passes through each of
the vertices.
The area of this rectangle is
4 × 5 = 20 units2
The area of the irregular
quadrilateral is found by
subtracting the area of each
of these triangles.
How can we find the area of this irregular
quadrilateral constructed on a pegboard?

24. Area of an irregular shapes on a pegboard
Area A = ½ × 2 × 3 = 3 units2
A B
C D
Area B = ½ × 2 × 4 = 4 units2
Area C = ½ × 1 × 2 = 1 units2
Area D = ½ × 1 × 3 = 1.5 units2
Total shaded area = 9.5 units2
Area of irregular quadrilateral
= (20 – 9.5) units2
= 10.5 units2
How can we find the area of this irregular
quadrilateral constructed on a pegboard?

25. Area of an irregular shape on a pegboard

26. Area of a triangle
What proportion of this rectangle has been shaded?
8 cm
4 cm
Drawing a line here might help.
What is the area of this triangle?
Area of the triangle = × 8 × 4 =
1
2
4 × 4 = 16 cm2

27. Area of a triangle

28. Area of a triangle
The area of any triangle can be found using the formula:
Area of a triangle = × base × perpendicular height
1
2
base
perpendicular height
Or using letter symbols:
Area of a triangle = bh
1
2

29. Area of a triangle
What is the area of this triangle?
Area of a triangle = bh
1
2
7 cm
6 cm
=
1
2
× 7 × 6
= 21 cm2

30. Area of a parallelogram

31. Area of a parallelogram
Area of a parallelogram = base × perpendicular height
base
perpendicular
height
The area of any parallelogram can be found using the formula:
Or using letter symbols:
Area of a parallelogram = bh

32. Area of a parallelogram
What is the area of this parallelogram?
Area of a parallelogram = bh
12 cm
7 cm
= 7 × 12
= 84 cm2
8 cm
We can ignore
this length

33. Area of a trapezium

34. Area of a trapezium
The area of any trapezium can be found using the formula:
Area of a trapezium = (sum of parallel sides) × height
1
2
Or using letter symbols:
Area of a trapezium = (a + b)h
1
2
perpendicular
height
a
b

35. Area of a trapezium
9 m
6 m
14 m
Area of a trapezium = (a + b)h
1
2
= (6 + 14) × 9
1
2
= × 20 × 9
1
2
= 90 m2
What is the area of this trapezium?

36. Area of a trapezium
What is the area of this trapezium?
Area of a trapezium = (a + b)h
1
2
= (8 + 3) × 12
1
2
= × 11 × 12
1
2
= 66 m2
8 m
3 m
12 m

37. Area problems
7 cm
10 cm
What is the area of the
yellow square?
We can work this out by subtracting
the area of the four blue triangles from
the area of the whole blue square.
If the height of each blue triangle is 7 cm, then the base is 3 cm.
Area of each blue triangle = ½ × 7 × 3
= ½ × 21
= 10.5 cm2
3 cm
This diagram shows a yellow square inside a blue square.

38. Area problems
7 cm
10 cm
We can work this out by subtracting
the area of the four blue triangles from
the area of the whole blue square.
There are four blue triangles so:
Area of four triangles = 4 × 10.5 = 42 cm2
Area of blue square = 10 × 10 = 100 cm2
Area of yellow square = 100 – 42 = 58 cm2
3 cm
This diagram shows a yellow square inside a blue square.
What is the area of the
yellow square?

39. Area formulae of 2-D shapes
You should know the following formulae:
b
h
Area of a triangle = bh
1
2
Area of a parallelogram = bh
Area of a trapezium = (a + b)h
1
2
b
h
a
h
b

40. Using units in formulae
Remember, when using formulae we must make sure that all
values are written in the same units.
For example, find the area of this trapezium.
76 cm
1.24 m
518 mm
Let’s write all the lengths in cm.
518 mm = 51.8 cm
1.24 m = 124 cm
Area of the trapezium = ½(76 + 124) × 51.8
= ½ × 200 × 51.8
= 5180 cm2
Don’t forget to
put the units at
the end.

41. Contents
S8 Perimeter, area and volume
A
A
A
A
A
A
S8.3 Surface area
S8.1 Perimeter
S8.6 Area of a circle
S8.2 Area
S8.5 Circumference of a circle
S8.4 Volume

42. To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The top and the bottom of the
cuboid have the same area.
Surface area of a cuboid

43. To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The front and the back of the
cuboid have the same area.
Surface area of a cuboid

44. To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The left hand side and the right
hand side of the cuboid have
the same area.
Surface area of a cuboid

45. To find the surface area of a shape, we calculate the
total area of all of the faces.
Can you work out the
surface area of this cuboid?
Surface area of a cuboid
7 cm
8 cm
5 cm
The area of the top = 8 × 5
= 40 cm2
The area of the front = 7 × 5
= 35 cm2
The area of the side = 7 × 8
= 56 cm2

46. To find the surface area of a shape, we calculate the
total area of all of the faces.
So the total surface area =
Surface area of a cuboid
7 cm
8 cm
5 cm
2 × 40 cm2
+ 2 × 35 cm2
+ 2 × 56 cm2
Top and bottom
Front and back
Left and right side
= 80 + 70 + 112 = 262 cm2

47. We can find the formula for the surface area of a cuboid
as follows.
Surface area of a cuboid =
Formula for the surface area of a cuboid
h
l
w
2 × lw Top and bottom
+ 2 × hw Front and back
+ 2 × lh Left and right side
= 2lw + 2hw + 2lh

48. How can we find the surface area of a cube of length x?
Surface area of a cube
x
All six faces of a cube have the
same area.
The area of each face is x × x = x2.
Therefore:
Surface area of a cube = 6x2

49. This cuboid is made from alternate purple and green
centimetre cubes.
Chequered cuboid problem
What is its surface area?
Surface area
= 2 × 3 × 4 + 2 × 3 × 5 + 2 × 4 × 5
= 24 + 30 + 40
= 94 cm2
How much of the
surface area is green?
47 cm2

50. What is the surface area of this L-shaped prism?
Surface area of a prism
6 cm
5 cm
3 cm
4 cm
3 cm
To find the surface area of
this shape we need to add
together the area of the two
L-shapes and the area of the
six rectangles that make up
the surface of the shape.
Total surface area
= 2 × 22 + 18 + 9 + 12 + 6
+ 6 + 15
= 110 cm2

51. 5 cm
6 cm
3 cm
6 cm
3 cm3 cm
3 cm
It can be helpful to use the net of a 3-D shape to calculate its
surface area.
Using nets to find surface area
Here is the net of a 3 cm by 5 cm by 6 cm cuboid.
Write down the
area of each
face.
15 cm2 15 cm2
18 cm2
30 cm2 30 cm2
18 cm2
Then add the
areas together
to find the
surface area.
Surface Area = 126 cm2

52. Here is the net of a regular tetrahedron.
Using nets to find surface area
What is its surface area?
6 cm
5.2 cm
Area of each face = ½bh
= ½ × 6 × 5.2
= 15.6 cm2
Surface area = 4 × 15.6
= 62.4 cm2

53. Contents
S8 Perimeter, area and volume
A
A
A
A
A
A
S8.4 Volume
S8.1 Perimeter
S8.6 Area of a circle
S8.2 Area
S8.5 Circumference of a circle
S8.3 Surface area

54. The following cuboid is made out of interlocking cubes.
Making cuboids
How many cubes does it contain?

55. We can work this out by dividing the cuboid into layers.
Making cuboids
The number of cubes in each layer
can be found by multiplying the
number of cubes along the length
by the number of cubes along the
width.
3 × 4 = 12 cubes in each layer.
There are three layers altogether
so the total number of cubes in the
cuboid = 3 × 12 = 36 cubes.

56. The amount of space that a three-dimensional object takes
up is called its volume.
Making cuboids
We can use mm3, cm3, m3 or km3.
The 3 tells us that there are three dimensions, length, width
and height.
Volume is measured in cubic units.
Liquid volume or capacity is measured in ml, l, pints or
gallons.

57. Volume of a cuboid
We can find the volume of a cuboid by multiplying the area of
the base by the height.
Volume of a cuboid
= length × width × height
= lwh
height, h
length, l
width, w
The area of the base
= length × width
So:

58. Volume of a cuboid
What is the volume of this cuboid?
Volume of cuboid
= length × width × height
= 13 × 8 × 5
= 520 cm3
5 cm
8 cm 13 cm

59. Volume and displacement

60. Volume and displacement
By dropping cubes and cuboids into a measuring cylinder
half filled with water we can see the connection between the
volume of the shape and the volume of the water displaced.
1 ml of water has a volume of 1 cm3
If an object is dropped into a measuring cylinder and
displaces 5 ml of water then the volume of the object is
5 cm3.
What is the volume of 1 litre of water?
1 litre of water has a volume of 1000 cm3.

61. What is the volume of this L-shaped prism?
Volume of a prism made from cuboids
6 cm
5 cm
3 cm
4 cm
3 cm
We can think of the shape as
two cuboids joined together.
Volume of the green cuboid
= 6 × 3 × 3 = 54 cm3
Volume of the blue cuboid
= 3 × 2 × 2 = 12 cm3
Total volume
= 54 + 12 = 66 cm3

62. Remember, a prism is a 3-D shape with the same
cross-section throughout its length.
Volume of a prism
We can think of this prism as lots
of L-shaped surfaces running
along the length of the shape.
Volume of a prism
= area of cross-section × length
If the cross-section has an area
of 22 cm2 and the length is 3 cm:
Volume of L-shaped prism = 22 × 3 = 66 cm3
3 cm

63. What is the volume of this triangular prism?
Volume of a prism
5 cm
4 cm
7.2 cm
Area of cross-section = ½ × 5 × 4 = 10 cm2
Volume of prism = 10 × 7.2 = 72 cm3

64. Volume of a prism
Area of cross-section = 7 × 12 – 4 × 3 = 84 – 12 =
Volume of prism = 5 × 72 = 360 m3
3 m
4 m
12 m
7 m
5 m
72 m2
What is the volume of this prism?

65. Contents
S8 Perimeter, area and volume
A
A
A
A
A
A
S8.5 Circumference of a circle
S8.1 Perimeter
S8.6 Area of a circle
S8.2 Area
S8.3 Surface area
S8.4 Volume

66. Circle circumference and diameter

67. The value of π
For any circle the circumference is always just over
three times bigger than the radius.
The exact number is called π (pi).
We use the symbol π because the number cannot be written
exactly.
π = 3.141592653589793238462643383279502884197169
39937510582097494459230781640628620899862803482
53421170679821480865132823066470938446095505822
31725359408128481117450284102701938521105559644
62294895493038196 (to 200 decimal places)!

68. Approximations for the value of π
When we are doing calculations involving the value π
we have to use an approximation for the value.
For a rough approximation we can use 3.
Better approximations are 3.14 or .22
7
We can also use the π button on a calculator.
Most questions will tell you which approximation to use.
When a calculation has lots of steps we write π as a symbol
throughout and evaluate it at the end, if necessary.

69. The circumference of a circle
For any circle:
π =
circumference
diameter
or:
We can rearrange this to make an formula to find the
circumference of a circle given its diameter.
C = πd
π =
C
d

70. The circumference of a circle
Use π = 3.14 to find the circumference of this circle.
C = πd
8 cm
= 3.14 × 8
= 25.12 cm

71. Finding the circumference given the radius
The diameter of a circle is two times its radius, or
C = 2πr
d = 2r
We can substitute this into the formula
C = πd
to give us a formula to find the circumference of a circle
given its radius.

72. The circumference of a circle
Use π = 3.14 to find the circumference of the following circles:
C = πd
4 cm
= 3.14 × 4
= 12.56 cm
C = 2πr9 m
= 2 × 3.14 × 9
= 56.52 m
C = πd
23 mm = 3.14 × 23
= 72.22 mm
C = 2πr
58 cm
= 2 × 3.14 × 58
= 364.24 cm

73. ?
Finding the radius given the circumference
Use π = 3.14 to find the radius of this circle.
C = 2πr
12 cm
How can we rearrange
this to make r the subject
of the formula?
r =
C
2π
12
2 × 3.14
≈
= 1.91 cm (to 2 d.p.)

74. Find the perimeter of this shape
Use π = 3.14 to find perimeter of this shape.
The perimeter of this shape is
made up of the circumference
of a circle of diameter 13 cm
and two lines of length 6 cm.
6 cm
13 cm
Perimeter = 3.14 × 13 + 6 + 6
= 52.82 cm

75. Circumference problem
The diameter of a bicycle wheel is 50 cm. How many
complete rotations does it make over a distance of 1 km?
50 cm
The circumference of the wheel
= 3.14 × 50
Using C = πd and π = 3.14,
= 157 cm
The number of complete rotations
= 100 000 ÷ 157
≈ 636
1 km = 100 000 cm

76. Contents
S8 Perimeter, area and volume
A
A
A
A
A
AS8.6 Area of a circle
S8.1 Perimeter
S8.2 Area
S8.5 Circumference of a circle
S8.3 Surface area
S8.4 Volume

77. Area of a circle

78. Formula for the area of a circle
We can find the area of a circle using the formula.
radius
Area of a circle = πr2
Area of a circle = π × r × r
or

79. The circumference of a circle
Use π = 3.14 to find the area of this circle.
A = πr24 cm
≈ 3.14 × 4 × 4
= 50.24 cm2

80. Finding the area given the diameter
The radius of a circle is half of its diameter, or
We can substitute this into the formula
A = πr2
to give us a formula to find the area of a circle given its
diameter.
r =
d
2
A =
πd2
4

81. The area of a circle
Use π = 3.14 to find the area of the following circles:
A = πr2
2 cm
= 3.14 × 22
= 12.56 cm2
A = πr2
10 m
= 3.14 × 52
= 78.5 m2
A = πr2
23 mm = 3.14 × 232
= 1661.06 mm2
A = πr2
78 cm
= 3.14 × 392
= 4775.94 cm2

82. Find the area of this shape
Use π = 3.14 to find area of this shape.
The area of this shape is made up
of the area of a circle of diameter
13 cm and the area of a rectangle
of width 6 cm and length 13 cm.
6 cm
13 cm Area of circle = 3.14 × 6.52
= 132.665 cm2
Area of rectangle = 6 × 13
= 78 cm2
Total area = 132.665 + 78
= 210.665 cm2

83. Area of a sector
What is the area of this sector?
72°
5 cm
Area of the sector =
72°
360°
× π × 52
1
5
= × π × 52
= π × 5
= 15.7 cm2 (to 1 d.p.)
We can use this method to find the area of any sector.

84. Area problem
Find the shaded area to 2 decimal places.
Area of the square = 12 × 12
1
4
Area of sector = × π × 122
= 36π
12 cm
= 144 cm2
Shaded area = 144 – 36π
= 30.96 cm2 (to 2 d.p.)