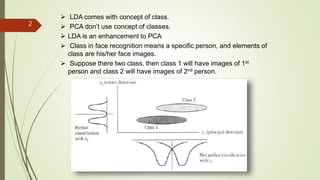
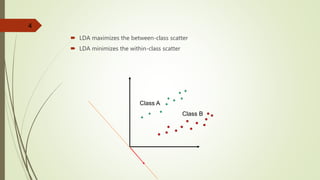
This document discusses linear discriminant analysis (LDA) for face recognition. It explains that LDA, unlike PCA, takes into account class labels to maximize between-class variance and minimize within-class variance when performing dimensionality reduction. The algorithm section describes how LDA computes within-class and between-class scatter matrices and finds the projection matrix by solving a generalized eigenvalue problem to maximize class separability. Recognition is done by projecting test faces onto the LDA space and running a nearest neighbor classifier to assign labels.

1. Linear Discriminant
Analysis
1

2. 2
 LDA comes with concept of class.
 PCA don’t use concept of classes.
 LDA is an enhancement to PCA
 Class in face recognition means a specific person, and elements of
class are his/her face images.
 Suppose there two class, then class 1 will have images of 1st
person and class 2 will have images of 2nd person.

3. 3
• Multiple classes and PCA
− Suppose there are C classes in the training data.
− PCA is based on the sample covariance which characterizes the
scatter of the entire data set, irrespective of class-membership.
− The projection axes chosen by PCA might not provide good
discrimination power.
• What is the goal of LDA?
− Perform dimensionality reduction while saving as much of the class
discriminatory information as possible.
− Search to find directions along which the classes are best separated.
− Takes into consideration the scatter within-classes but also the
scatter between-classes.

4. 4
 LDA maximizes the between-class scatter
 LDA minimizes the within-class scatter
Class A
Class B

5. 5 Algorithm
 Assumptions
 Square images with Width=Height=N
 M is the number of images in the database
 P is the number of persons in the database

6. 6
 The database
2
1
2
N
b
b
b
 
 
 
 
  
 
M
2
1
2
N
c
c
c
 
 
 
 
  
 
M
2
1
2
N
d
d
d
 
 
 
 
  
 
M
2
1
2
N
e
e
e
 
 
 
 
  
 
M
2
1
2
N
a
a
a
 
 
 
 
  
 
M
2
1
2
N
f
f
f
 
 
 
 
  
 
M
2
1
2
N
g
g
g
 
 
 
 
  
 
M
2
1
2
N
h
h
h
 
 
 
 
  
 
M

7. 7
Fisherfaces, the algorithm
 We compute the average of all faces
2 2 2
1 1 1
2 2 21
, 8
N N N
a b h
a b h
m where M
M
a b h
   
 
    
 
     
L
Lr
M M M
L

8. 8
Fisherfaces, the algorithm
 Compute the average face of each person
2 2 2 2
2 2 2 2
1 1 1 1
2 2 2 2
1 1 1 1
2 2 2 2
1 1
, ,
2 2
1 1
,
2 2
N N N N
N N N N
a b c d
a b c d
x y
a b c d
e f g h
e f g h
z w
e f g h
    
   
     
   
          
    
   
     
   
          
r r
M M M M
rr
M M M M

9. 9
Fisherfaces, the algorithm
 And subtract them from the training faces
2 2 2 2 2 2 2 2
2 2
1 1 1 1 1 1 1 1
2 2 2 2 2 2 2 2
1 1 1 1
2 2
, , , ,
,
m m m m
N N N N N N N N
m m
N N
a x b x c y d y
a x b x c y d y
a b c d
a x b x c y d y
e z f z
e z f
e f
e z
          
       
             
       
                        
  
 
  
 
   
r rr r
M M M M M M M M
rr
M M
2 2 2 2 2 2
1 1 1 1
2 2 2 2 2 2
, ,m m
N N N N N N
g w h w
z g w h w
g h
f z g w h w
      
     
        
     
                 
rr
M M M M M M

10. 10
Fisherfaces, the algorithm
 We build scatter matrices S1, S2, S3, S4
 And the within-class scatter matrix SW
   
   
1 2
3 4
, ,
,
m m m m m m m m
m m m m m m m m
S a a b b S c c d d
S e e f f S g g h h
   
   
   
   
r r r rr r r r
r r r rr r r r
1 2 3 4WS S S S S   

11. Fisherfaces, the algorithm
 The between-class scatter matrix
 We are searching the matrix W maximizing
           2 2 2 2BS x m x m y m y m z m z m w m w m
   
           
r r r r r r r r r r r r r rr r
 
B
W
W S W
J W
W S W




12. 12
Fisherfaces, the algorithm
 Columns of W are eigenvectors of
 We have to compute the inverse of SW
 We have to multiply the matrices
 We have to compute the eigenvectors
1
W BS S

13. 13
Recognition
 Project faces onto the LDA-space
 To classify the face
 Project it onto the LDA-space
 Run a nearest-neighbor classifier
 Nearest is our answer