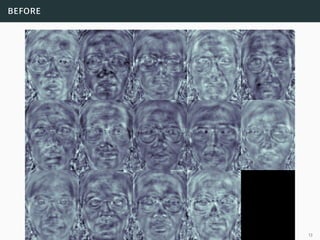
The document discusses the Fisherfaces face recognition algorithm, which improves upon the Eigenfaces method by using Fisher's Linear Discriminant Analysis for better discrimination of facial features. It highlights the importance of input data quality and discusses the algorithm's performance in various illumination conditions. Key mathematical formulations related to class separability and transformation matrices are also presented.

1. fisherfaces
Face recognition algorithm
Vishnu K N S5 CSE B 59
Federal Institute of Science and Technology

2. introduction
Face Recognition System
-The input of a face recognition system is always an image or video
stream.
-The output is an identification or verification of the subject or
subjects that appear in the image or video.
1

3. fisherfaces

4. working
-The Fisherfaces method learns a class-specifc transformation
matrix, so they do not capture illumination as obviously as the
Eigenfaces method.
-The Discriminant Analysis instead fnds the facial features to
discriminate betweenthe persons.
3

5. -It’s important to mention, that the performance of the Fisherfaces
heavily depends on the input data as well.
-Practically said: if you learn the Fisherfaces for well-illuminated
pictures only and you try to recognize faces in bad-illuminated
scenes, then method is likely to fnd the wrong components (just
because those features may not be predominant on bad illuminated
images).
4

6. The Fisherfaces allow a reconstruction of the projected image, just
like the Eigenfaces did.
But since we only identifed the features to distinguish between
subjects, you can’t expect a nice reconstruction of the original image.
For the Fisherfaces method we’ll project the sample image onto
each of the Fisherfaces instead.
5

7. fisherfaces v/s eigenfaces
-The Eigenface method uses Principal Component Analysis (PCA) to
linearly project the image space to a low dimensional feature space.
-The Fisherface method is an enhancement of the Eigenface method
that it uses Fisher’s Linear Discriminant Analysis (FLDA or LDA) for
the dimensionality reduction.
6

8. -The LDA maximizes the ratio of between-class scatter to that of
within-class scatter, therefore, it works better than PCA for purpose
of discrimination.
-The Fisherface is especially useful when facial images have large
variations in illumination and facial expression.
7

9. algorithm

10. Let X be a random vector with samples drawn from c classes:
X = {X1, X2, . . . , Xc}
Xi = {x1, x2, . . . , xn}
The scatter matrices SBandSWarecalculatedas :
SB =
c∑
i=1
Ni(µi − µ)(µi − µ)T
SW =
c∑
i=1
∑
xj∈Xi
(xj − µi)(xj − µi)T
9

11. , where µisthetotalmean :
µ = 1
N
∑N
i=1 xi
And µiisthemeanofclassi ∈ {1, . . . , c} :
µi = 1
|Xi|
∑
xj∈Xi
xj
10

12. Fisher’s classic algorithm now looks for a projection W, that
maximizes the class separability criterion:
Wopt = arg maxW
|WT
SBW|
|WTSWW|
a solution for this optimization problem is given by solving the
General Eigenvalue Problem:
SBvi = λiSwvi
S−1
W SBvi = λivi
11

13. The optimization problem can then be rewritten as:
Wpca = arg maxW |WT
STW|
Wfld = arg maxW
|WT
WT
pcaSBWpcaW|
|WTWT
pcaSWWpcaW|
The transformation matrix W, that projects a sample into the
(c-1)-dimensional space is then given by:
W = WT
fldWT
pca
12

14. before
13

15. after
14

16. thank you