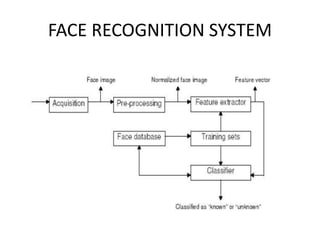
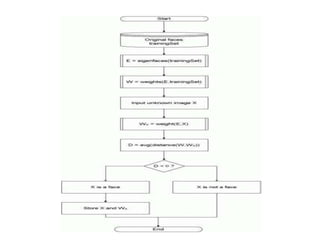
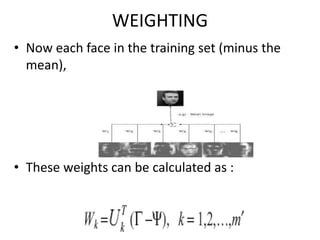
The document discusses the eigenface approach to face recognition, detailing its reliance on principal component analysis (PCA) for extracting facial features and distinguishing between unique identities. It covers the stages of face recognition, the advantages and disadvantages of the eigenface method, and potential applications such as security and identification. The study concludes that eigenfaces effectively reduce image size while capturing significant distinguishing features for classification and recognition.

1. “FACE RECOGNITION USING EIGENFACES”
Dr.Sachin.S.Gurav
.

2. Index
• INTRODUCTION
• FACE RECOGNITION SYSTEM
• EIGENFACE APPROACH
• EIGEN VALUES AND EIGEN VECTORS
• CALCULATIONS OF EIGEN VALUES AND EIGEN
VECTORS
• ALGORITH TO FIND EIGENFACES
• EIGENFACES METHOD
• ADVANTAGE AND DISADVENTAGE
• APPLICATIONS
• CONCLUSION
• REFERENCES

3. Introduction
Problem Statement :
• Given an image, to identify it as a face and/or
extract face images from it.
• To retrieve the similar images (based on a
heuristic)from the given database of face
images.

4. Introduction
• Face recognition based on information theory approach of
coding and decoding the face image.
• Proposed methodology is connection of two stages –
• Eigenface approach uses Principal Component Analysis (PCA)
algorithm.
• dynamic images-- images received from the camera.
• static images – modified image.
• Eigenfaces- The scheme is based on an information theory
approach that decomposes face images into a small set of
characteristic feature images
• face recognition techniques can be divided into two-
1) Appearance-based
2) Feature-based,

5. Face Recognition
• Face recognition is the process of putting a name to a face. Once
you've detected a face, face recognition means figuring out whose
face it is
• Face is the most common biometric used by humans
• Applications range from static, mug-shot verification to a dynamic,
uncontrolled face identification in a cluttered background
• Challenges:
• automatically locate the face
• recognize the face from a general view point under different
illumination conditions, facial expressions, and aging effects

6. FACE RECOGNITION SYSTEM

7. There are six main functional blocks
A. The acquisition module
B. The pre-processing module
C. The feature extraction module
D. The classification module
E. Training set
F. Face database

8. Stages of Face Recognition
(1) face location detection
(2) feature extraction
(3) facial image classification
Approaches of Feature Extraction
(1) local feature : eyes, nose, mouth information
easily affected by irrelevant information .
(2) global feature :
extract feature from whole image .

9. Authentication vs Identification
• Face Authentication/Verification
• Face Identification/Recognition

11. EIGENFACE APPROACH
• Extract the relevant facial information, which
may or may not be directly related to human
intuition of face features such as the eyes,
nose, and lips.
• Represent face images efficiently. To reduce
the computation and space complexity.

12. EIGEN VALUES AND EIGEN VECTORS
• In this shear mapping of the Mona Lisa fig A a, the picture
was deformed in such away that its central vertical axis (red
vector)has not changed direction, but the diagonal vector
(blue) has changed direction. Hence the red vector is an
eigenvector of the transformation and the blue vector is
not. Since the red vector was neither stretched nor
compressed, its eigenvalue is 1.

13. CALCULATIONS OF EIGEN
VALUES AND EIGEN VECTORS
• The vector x is an eigenvector of the matrix A
with eigenvalue λ (lambda) if the following
equation holds:
Ax=λx
where

14. Eigen values
• This equation can be interpreted geometrically as
follows: a vector x is an eigenvector if
multiplication by A stretches, shrinks, leaves
unchanged, flips (points in the opposite
direction), flips and stretches, or flips and shrinks
x.
• 1) If the eigenvalue λ > 1, x is stretched by this
factor.
• 2) If λ = 1, the vector x is not affected at all by
multiplication by A.
• 3) If 0 < λ < 1, x is shrunk (or compressed).

15. ALGORITHM TO FIND EIGENFACES
1. Obtain M training images , I1 I2 I3 I4 I5 … IM , it is
very important that the images are centered.

16. 2. Represent each Ii image as a vector Гi as
discussed above.

17. • 3. Find the average face vector Ψ.

18. 4. Subtract the mean face from each face vector
Гi to get a set of vectors Фi .The purpose of
subtracting the mean image from each image
vector is to be left with only the distinguishing
features from each face and “removing” in a
way information that is common.
Фi = Гi - Ψ.

19. 5. Find the Covariance matrix C:
Where
Here note that C is N2×N2 matrix & A is N2×M matrix

20. • We now need to calculate the Eigenvectors of
C , However note that C is a N2×N2 matrix and
it would return N2 Eigenvectors each being N2
dimensional. For an image this number is
HUGE. The computations required would
easily make your system run out of memory.

21. 6) Instead of matrix AAT consider matrix ATA
.remember A is a N2×M matrix thus ATA is a
M×M matrix
• M Eigen vectors of dimension M×1 lets call
these as Vi

22. • 7. Now from some properties of matrices, it
follows that A vi. We have found out vi. earlier.
This implies that using vi we can calculate the
M largest Eigenvectors. Remember that as M
is simply the number of training images.

23. 8. Find the best M Eigenvectors of C=AAT by
using the relation discussed above.
9. Select the best Eigenvectors, the selection of
these Eigenvectors is done heuristically

24. EIGEN FACES
• The Eigenvectors found at the end of the previous
section, when converted to a matrix in a process
that is reverse to that in , have a face like
appearance.
• Since these are Eigenvectors and have a face like
appearance, they are called Eigen faces.
Sometimes, they are also called as Ghost Images
because of their weird appearance.

25. EIGEN VECTORS CONVERTED TO
MATRIX FORM

26. WEIGHTING
• Now each face in the training set (minus the
mean),
• These weights can be calculated as :

27. • The Euclidean distance between two weight
vectors d(Ωi, Ωj) provides a measure of similarity
between the corresponding images i and j. If the
Euclidean distance between
ГNEW and other faces exceeds - on average - some
threshold value θ, one can assume
• that ГNEW is no face at all.
er < θ image recognized
er > θ image not recognized

28. Why is the Threshold im?

29. Advantages
• Eigen method distills the large dimension
images to Eigen vector which reduces the
processing time .
• Less memory storage .

30. Disadvantages
•Not able to discriminate between
twins
* Orientation of face
* Time consumption

31. Application
• Voter id
• ATM security
• Airport security purpose
• Offices
• Crime investigation
• Access Control

32. Future Scope
• Face Detection in motion pictures.
• Investigate whether eigenfaces is a good
solution for this problem by comparing with
other feature extraction techniques such as
DCT.

33. CONCLUSION
»In this study, we used the eigenfaces to represent the
features vectors for human faces.
»The features are extracted from the original image to
represents unique identity used in classification and
recognition.
» The eigenfaces has proven the capability to provide
the significant features and reduces the input size