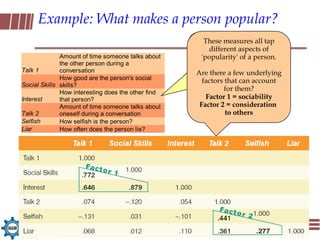
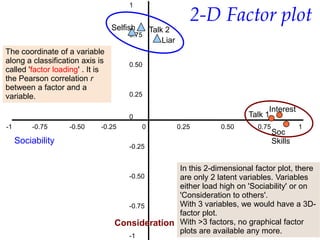
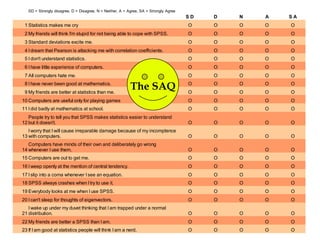
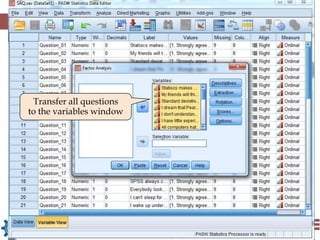
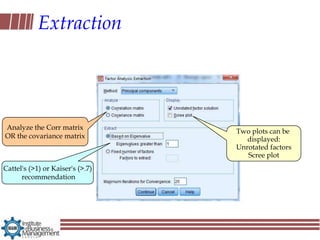
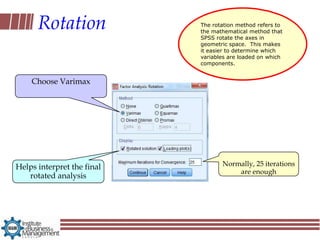
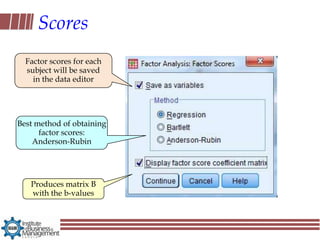
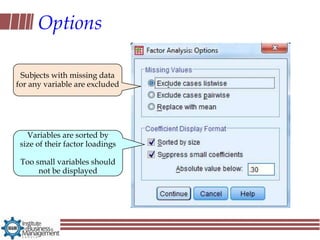
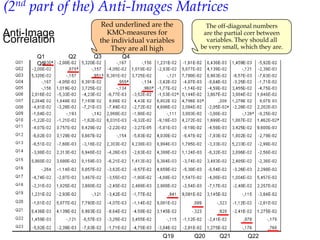
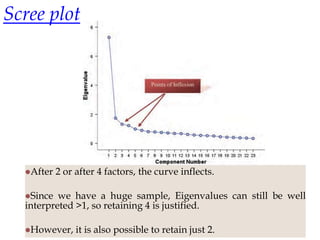
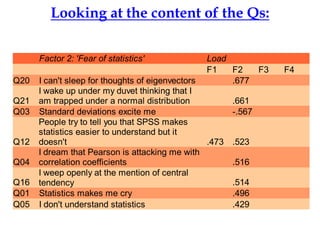
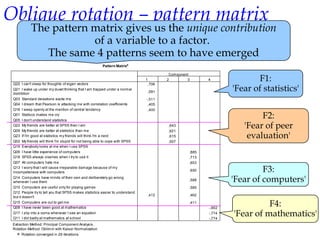
Exploratory factor analysis is a technique used to identify underlying factors or latent variables that explain the pattern of correlations within a set of observed variables. It has three main uses: to understand the structure of variables, to construct questionnaires, and to reduce large datasets. The example document describes constructing a questionnaire called the "SPSS-Anxiety Questionnaire" to measure anxiety towards learning the statistical software SPSS. It discusses initial considerations like sample size and data screening that are important before performing factor analysis.

1. Exploratory factor analysis
Dr. M. Shakaib Akram
Note: Most of the material used in this lecture has been taken from “Discovering
Statistics Using SPP” by Andy Field, 3rd Ed
.

2. What is factor analysis?
Factor analysis (and principal component analysis)
is a technique for identifying groups or clusters of
variables underlying a set of measures.
Those variables are called 'factors', or 'latent
variables' since they are not directly observable,
e.g., 'intelligence'.
A 'latent variable' is “a variable that cannot be
directly measured, but is assumed to be related to
several variables that can be measured.“ (Glossary,
p 736)

3. What is factor analysis used for?
Factor analysis has 3 main uses:
To understand the structure of a set of
variables, e.g., intelligence
To construct a questionnaire to measure
an underlying variable
To reduce a large data set to a more
manageable size

4. The most basic data basis
R-matrix
An R-matrix is simply a correlation matrix
with Pearson r-coefficients between pairs
of variables as the off-diagonal elements.
In factor analysis one tries to find latent
variables that underlie clusters of
correlations in such an R-matrix.

5. Example: What makes a person popular?
These measures all tap
These measures all tap
different aspects of
different aspects of
Amount of time someone talks about 'popularity' of aaperson.
'popularity' of person.
the other person during a
Talk 1 conversation
Are there aafew underlying
Are there few underlying
How good are the person's social factors that can account
Social Skills skills? factors that can account
How interesting does the other find
for them?
for them?
Interest that person? Factor 1 = sociability
Amount of time someone talks about Factor 2 = consideration
Talk 2 oneself during a conversation to others
Selfish How selfish is the person?
Liar How often does the person lie?

6. Graphical representations of factors
Factors can be visualized as axes along which
we can plot variables.
The coordinates of variables along each axis
represents the strength of the relationship
between that variable and each factor. In our
expl., we have 2 underlying factors.
The axis line ranges from -1 to +1, which is
the range of possible correlations r.
The position of a variable depends on its
correlation coefficient with the 2 factors.

7. 1
Selfish
2-D Factor plot
Talk 2
0.75
Liar
The coordinate of a variable
along a classification axis is 0.50
called 'factor loading' . It is
the Pearson correlation r
between a factor and a
variable. 0.25
Interest
0 Talk 1
-1 -0.75 -0.50 -0.25 0 0.25 0.50 0.75 1
Soc
Sociability Skills
-0.25
In this 2-dimensional factor plot, there
-0.50 are only 2 latent variables. Variables
either load high on 'Sociability' or on
'Consideration to others'.
-0.75 With 3 variables, we would have a 3D-
factor plot.
Consideration With >3 factors, no graphical factor
plots are available any more.
-1

8. Research example: The ‘SPSS-Anxiety Questionnaire' SAQ
One use of Factor Analysis is constructing
questionnaires.
With the SAQ, students' anxiety towards
SPSS shall be measured, using 23 questions.
The questionnaire can be used to predict individuals'
anxiety towards learning SPSS.
Furthermore, the factor structure behind 'anxiety to use
SPSS' shall be explored: which latent variables contribute to
anxiety about SPSS?

9. SD = Strongly disagree, D = Disagree, N = Neither, A = Agree, SA = Strongly Agree
SD D N A SA
1 Statistics makes me cry O O O O O
2 My friends will think I'm stupid for not being able to cope with SPSS. O O O O O
3 Standard deviations excite me. O O O O O
4 I dream that Pearson is attacking me with correlation coefficients. O O O O O
5 I don't understand statistics. O O O O O
6 I have little experience of computers. O O O O O
7 All computers hate me. O O O O O
8 I have never been good at mathematics.
9 My friends are better at statistics than me.
The SAQ O
O
O
O
O
O
O
O
O
O
10 Computers are useful only for playing games O O O O O
11 I did badly at mathematics at school. O O O O O
People try to tell you that SPSS makes statistics easier to understand
12 but it doesn't. O O O O O
I worry that I will cause irreparable damage because of my incomptence
13 with computers. O O O O O
Computers have minds of their own and deliberately go wrong
14 whenever I use them. O O O O O
15 Computers are out to get me. O O O O O
16 I weep openly at the mention of central tendency. O O O O O
17 I slip into a coma whenever I see an equation. O O O O O
18 SPSS always crashes when I try to use it. O O O O O
19 Everybody looks at me when I use SPSS. O O O O O
20 I can't sleep for thoughts of eigenvectors. O O O O O
I wake up under my duvet thinking that I am trapped under a normal
21 distribution. O O O O O
22 My friends are better a SPSS than I am. O O O O O
23 If I am good at statistics people will think I am a nerd. O O O O O

10. Initial considerations: sample size
The reliability of factor analysis relies on the sample size.
As a 'rule of thumb', there should be 10-15 subjects per
variable.
The stability of a factor solution depends on:
1. Absolute sample size
2. Magnitude of factor loading (>.6)
3. Communalities (>.6; the higher the better)
The KMO*-measure is the ratio of the squared correlation
between variables to the squared partial correlation
between variables. It ranges from 0-1. Values between .7
and .8 are good. They suggest a factor analysis.
*KMO: Kaiser-Meyer-Olkin measure of sampling adequacy

11. Data screening
 The variables in the questionnaire should intercorrelate if they
measure the same thing. Questions that tap the same sub-
variable, e.g., worry, intrusive thoughts, or physiological
arousal, should be highly correlated.
 If there are questions that are not intercorrelated with others,
they should not be entered into the factor analysis.
 If questions correlate too highly, extreme multi-collinearity or
even singularity (perfectly correlated variables) result.
Too low and too high intercorrelations should be avoided.
 Finally, variables should be roughly normally distributed.

12. Running the analysis
(using SAQ.sav)
 Analyze Data Reduction Factor ...
To compute a principal
component analysis in SPSS,
select the Dimension Reduction
| Factor… command from the
Analyze menu.

13. Transfer all questions
to the variables window

14. Descriptives
First, mark the Univariate
Second, keep the descriptives checkbox to get
Initial solution mean & Std. Deviation etc.
checkbox to get the
statistics needed to
determine the number
of factors to extract.
Third, mark the Fifth, mark the Anti-image
Coefficients checkbox to checkbox to assess the
get a correlation matrix, appropriateness of factor
one of the outputs analysis for the variables.
needed to assess the
appropriateness of
factor analysis for the
variables.
The determinant Fourth, mark the KMO and Bartlett’s test
Sixth, click
should be of sphericity checkbox to assess the
on the
> .00001 appropriateness of factor analysis for the
Continue
variables.
button.

15. Extraction
First, click on the
Extraction… button to
specify statistics to
include in the output.
The extraction method refers
to the mathematical method
that SPSS uses to compute the
factors or components.

16. Extraction
Choose Principal components
Other options:

17. Extraction
Analyze the Corr matrix
Two plots can be
OR the covariance matrix displayed:
Unrotated factors
Scree plot
Cattel's (>1) or Kaiser's (>.7)
recommendation

18. Rotation The rotation method refers to
the mathematical method that
SPSS rotate the axes in
geometric space. This makes
it easier to determine which
variables are loaded on which
components.
Choose Varimax
Helps interpret the final Normally, 25 iterations
are enough
rotated analysis

19. Scores
Factor scores for each
subject will be saved
in the data editor
Best method of obtaining
factor scores:
Anderson-Rubin
Produces matrix B
with the b-values

20. Options
Subjects with missing data
for any variable are excluded
Variables are sorted by
size of their factor loadings
Too small variables should
not be displayed

21. Run the Factor Analysis
 Then rerun it again, this time changing the rotation to
oblique rotation: 'Direct Oblimin'
Choose 'Direct Oblimin'
this time
The output will be the same except for the rotation.

22. Interpreting output from SPSS
Preliminary analysis:
–data screening
–assumption testing
–sampling adequacy

23. 'Univariate Descriptives„: Mean, SD, and no. of sample

24. Correlation Matrix Q01 Q02 Q03
Correlation Matrixa
Q04 Q05 Q19 Q20 Q21 Q22 Q23
Correlation Q01 1,000 -,099 -,337 ,436 ,402 -,189 ,214 ,329 -,104 -,004
Q02 -,099 1,000 ,318 -,112 -,119 ,203 -,202 -,205 ,231 ,100
Q03 -,337 ,318 1,000 -,380 -,310 ,342 -,325 -,417 ,204 ,150
Q04 ,436 -,112 -,380 1,000 ,401 -,186 ,243 ,410 -,098 -,034
Q05 ,402 -,119 -,310 ,401 1,000 -,165 ,200 ,335 -,133 -,042
Q06 ,217 -,074 -,227 ,278 ,257 -,167 ,101 ,272 -,165 -,069
Selected output Q07
Q08
,305 -,159 -,382 ,409 ,339 -,269 ,221 ,483 -,168 -,070
for Q-5; 19-23
,331 -,050 -,259 ,349 ,269 -,159 ,175 ,296 -,079 -,050
Q09 -,092 ,315 ,300 -,125 -,096 ,249 -,159 -,136 ,257 ,171
Q10 ,214 -,084 -,193 ,216 ,258 -,127 ,084 ,193 -,131 -,062
Q11 ,357 -,144 -,351 ,369 ,298 -,200 ,255 ,346 -,162 -,086
Labels of questions Q12
Q13
,345
,355
-,195
-,143
-,410
-,318
,442
,344
,347
,302
-,267
-,227
,298
,204
,441
,374
-,167
-,195
-,046
-,053
omitted Q14
Q15
,338
,246
-,165
-,165
-,371
-,312
,351
,334
,315
,261
-,254
-,210
,226
,206
,399
,300
-,170
-,168
-,048
-,062
Q16 ,499 -,168 -,419 ,416 ,395 -,267 ,265 ,421 -,156 -,082
Q17 ,371 -,087 -,327 ,383 ,310 -,163 ,205 ,363 -,126 -,092
These are the Q18
Q19
,347
-,189
-,164
,203
-,375
,342
,382
-,186
,322
-,165
-,257
1,000
,235
-,249
,430
-,275
-,160
,234
-,080
,122
Pearson corr Q20 ,214 -,202 -,325 ,243 ,200 -,249 1,000 ,468 -,100 -,035
coefficients between
Q21 ,329 -,205 -,417 ,410 ,335 -,275 ,468 1,000 -,129 -,068
Q22 -,104 ,231 ,204 -,098 -,133 ,234 -,100 -,129 1,000 ,230
all pairs of variables Sig. (1-tailed)
Q23
Q01
-,004 ,100
,000
,150
,000
-,034
,000
-,042
,000
,122
,000
-,035
,000
-,068
,000
,230
,000
1,000
,410
Q02 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q03 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q04 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,043
Q05 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,017
These are the Q06
Q07
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
Significance levels Q08
Q09
,000
,000
,006
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,005
,000
for all correlations. Q10 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,001
Q11
Note: they are almost
,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q12 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,009
all significant! Q13
Q14
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,000
,004
,007
Q15 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,001
Q16 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q17 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q18 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q19 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q20 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,039
Q21
Determinant:
,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q22 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
.0005271 Q23 ,410
a. Determinant = 5,271E-04
,000 ,000 ,043 ,017 ,000 ,039 ,000 ,000
OK!

25. Scanning the Correlation Matrix Correlation Matrixa
Q01 Q02 Q03 Q04 Q05 Q19 Q20 Q21 Q22 Q23
Correlation Q01 1,000 -,099 -,337 ,436 ,402 -,189 ,214 ,329 -,104 -,004
Q02 -,099 1,000 ,318 -,112 -,119 ,203 -,202 -,205 ,231 ,100
Q03 -,337 ,318 1,000 -,380 -,310 ,342 -,325 -,417 ,204 ,150
Q04 ,436 -,112 -,380 1,000 ,401 -,186 ,243 ,410 -,098 -,034
Q05 ,402 -,119 -,310 ,401 1,000 -,165 ,200 ,335 -,133 -,042
2. Then scan the corr Q06
Q07
,217
,305
-,074
-,159
-,227
-,382
,278
,409
,257
,339
-,167
-,269
,101
,221
,272
,483
-,165
-,168
-,069
-,070
coefficients for >.9 Q08
Q09
,331 -,050 -,259 ,349 ,269 -,159 ,175 ,296 -,079 -,050
-,092 ,315 ,300 -,125 -,096 ,249 -,159 -,136 ,257 ,171
none! Q10 ,214 -,084 -,193 ,216 ,258 -,127 ,084 ,193 -,131 -,062
no problem with
Q11 ,357 -,144 -,351 ,369 ,298 -,200 ,255 ,346 -,162 -,086
Q12 ,345 -,195 -,410 ,442 ,347 -,267 ,298 ,441 -,167 -,046
multicollinearity Q13
Q14
,355
,338
-,143
-,165
-,318
-,371
,344
,351
,302
,315
-,227
-,254
,204
,226
,374
,399
-,195
-,170
-,053
-,048
Q15 ,246 -,165 -,312 ,334 ,261 -,210 ,206 ,300 -,168 -,062
Q16 ,499 -,168 -,419 ,416 ,395 -,267 ,265 ,421 -,156 -,082
Q17 ,371 -,087 -,327 ,383 ,310 -,163 ,205 ,363 -,126 -,092
Look for many low Q18
Q19
,347
-,189
-,164
,203
-,375
,342
,382
-,186
,322
-,165
-,257
1,000
,235
-,249
,430
-,275
-,160
,234
-,080
,122
correlations (p > .05) Q20
Q21
,214
,329
-,202
-,205
-,325
-,417
,243
,410
,200
,335
-,249
-,275
1,000
,468
,468
1,000
-,100
-,129
-,035
-,068
for a single variable Q22
Q23
-,104
-,004
,231
,100
,204
,150
-,098
-,034
-,133
-,042
,234
,122
-,100
-,035
-,129
-,068
1,000
,230
,230
1,000
none! Sig. (1-tailed) Q01 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,410
Q02 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q03 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q04 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,043
Q05 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,017
Q06 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q07 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q08 ,000 ,006 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,005
Q09
All Q seem to
,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q10 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,001
be fine!
Q11 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q12 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,009
Q13 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,004
Q14 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,007
Q15 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,001
Q16 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q17 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q18 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q19 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q20 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,039
Q21 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q22 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000 ,000
Q23 ,410 ,000 ,000 ,043 ,017 ,000 ,039 ,000 ,000
a. Determinant = 5,271E-04

26. Bartlett's test of sphericity
KMO statistics
KMO-measures >.9
KMO and Bartlett's Test are superb!
Kaiser-Meyer-Olkin Measure of Sampling KMO measures the ratio of the squared
Adequacy. ,930 correlation between variables
Bartlett's Test of Approx. Chi-Square 19334,492
to the squared partial correlation
Sphericity df 253 between variables.
Sig. ,000
KMO measures for
individual factors are
Bartlett's test tests if the R-matrix is an produced on the diagonal
identity matrix (matrix with only 1's in the of the anti-image corr
diagonal and 0's off-diagonal). However, matrix
we want to have correlated variables, so The KMO-measures
the off-diagonal elements should NOT be give us a hint at
0. Thus, the test should be significant, which variables should
i.e., the R-matrix should NOT be an be excluded from
identity matrix. the factor analysis

27. (2nd part of the) Anti-Images Matrices
Red underlined are the The off-diagonal numbers
Anti-Image KMO-measures for are the partial corr between
Correlation the individual variables variables. They should all
They are all high be very small, which they are.
Q1 Q2 Q3 Q4
Q5....
Q19 Q20 Q21 Q22

28. Before Initial eigenvalues and
extraction,
there are
as many
explained variances are
ordered in decreasing
Factor extraction
magnitude
factors
as there
are
variables, Before extraction After extraction After rotation
n=23 Total Variance Explained
Initial Eigenvalues Extraction Sums of Squared Loadings Rotation Sums of Squared Loadings
Component Total % of Variance Cumulative % Total % of Variance Cumulative % Total % of Variance Cumulative %
1 7,290 31,696 31,696 7,290 31,696 31,696 3,730 16,219 16,219
2 1,739 7,560 39,256 1,739 7,560 39,256 3,340 14,523 30,742
3 1,317 5,725 44,981 1,317 5,725 44,981 2,553 11,099 41,842
4 1,227 5,336 50,317 1,227 5,336 50,317 1,949 8,475 50,317
5 ,988 4,295 54,612
6 ,895 3,893 58,504
7 ,806 3,502 62,007 Only 4 factors Rotation optimizes
8 ,783 3,404 65,410
with an eigenvalue factor structure
9 ,751 3,265 68,676
10 ,717 3,117 71,793 > 1 are retained (Varimax).
The relative impor-
(Fisher's criterion)
11 ,684 2,972 74,765
12 ,670 2,911 77,676 tance of factors is
13
14
,612
,578
2,661
2,512
80,337
82,849
equalized. The
15 ,549 2,388 85,236 explained variance
16 ,523 2,275 87,511 of the 4 factors
17
18
,508
,456
2,210
1,982
89,721
91,704
is more similar
19 ,424 1,843 93,546 after rotation.
20 ,408 1,773 95,319
21 ,379 1,650 96,969
22 ,364 1,583 98,552
23 ,333 1,448 100,000
Extraction Method: Principal Component Analysis.

29. Communalities Before and after
extraction
Communalities
E.g.: 43,5% of variance in
Initial Extraction
Q01 1,000 ,435 Q1 is common, shared
Communality is the Q02 1,000 ,414 variance
Q03 1,000 ,530
proportion of common variance Q04 1,000 ,469
within a variable. Q05 1,000 ,343 Before extraction, there are
Q06 1,000 ,654
as many factors as there are
Initially, communality is Q07 1,000 ,545
variables, n=23, so that all
assumed to be 1 ('all variance is Q08
Q09
1,000
1,000
,739
,484 variance is explained by the
common'). Q10 1,000 ,335
factors and communality is
Q11 1,000 ,690
After extraction, the true Q12 1,000 ,513 1. (No data reduction yet).
communalities can be judged Q13 1,000 ,536 After extraction, some of the
better.
Q14 1,000 ,488 factors are retained, others
Q15 1,000 ,378
Q16 1,000 ,487
are dismissed. This leads to
Q17 1,000 ,683 a welcome data reduction.
Q18 1,000 ,597 Now the amount of variation
Q19
Q20
1,000
1,000
,343
,484
in each variable explained
Q21 1,000 ,550 by the factors is the
Q22 1,000 ,464 communality.
Q23 1,000 ,412
Extraction Method: Principal Component Analysis.

30. Before rotation, most variables loaded
highest on the first factor (which Component matrix
can therefore explain a high amount
of variation (31,7%)
Component Matrixa
Component
1 2 3 4
Q18 ,701
Q07 ,685 Loadings <.3
are suppressed, The component matrix shows the factor
Q16 ,679
Q13 ,673 hence the
Q12 ,669
blank spaces.
loadings of each variable before rotation.
Q21 ,658 SPSS has already extracted 4 components
Q14 ,656
Q11 ,652 -,400 (factors).
Q17 ,643
Q04 ,634
Q03 -,629 How can we decide how many factors we
Q15
Q01
,593
,586
should retain?
Q05 ,556
Q08 ,549 ,401 -,417
Q10 ,437 scree plot
Q20 ,436 -,404
Q19 -,427
Q09 ,627
Q02 ,548
Q22 ,465
Q06 ,562 ,571
Q23 ,507
Extraction Method: Principal Component Analysis.
a. 4 components extracted.

31. Scree plot
After 2 or after 4 factors, the curve inflects.
Since we have a huge sample, Eigenvalues can still be well
interpreted >1, so retaining 4 is justified.
However, it is also possible to retain just 2.

32. Rotated component matrix: orthogonal rotation
a
Rotated Component Matrix
Component
1 2 3 4
Q06 ,800
Q18 ,684
Q13 ,647 The Rotated component matrix has the same
Q07 ,638
Q14 ,579 information as the component matrix, only that
Q10
Q15
,550
,459
it is calculated after orthogonal rotation (here
Q20 ,677 with VARIMAX).
Q21 ,661
Q03 -,567
Q12 ,473 ,523
Q04 ,516
Loadings <.3
Q16 ,514
Q01 ,496
are suppressed,
Q05 ,429 hence the
Q08 ,833 blank spaces.
Q17 ,747
Q11 ,747
Q09 ,648
Q22 ,645
Q23 ,586
Q02 ,543
Q19 ,427
Extraction Method: Principal Component Analysis.
Rotation Method: Varimax with Kaiser Normalization.
a. Rotation converged in 9 iterations.

33. Component vs. Rotated Component Matrix
a
Rotated Component Matrix
Component Matrixa
Component
Component
1 2 3 4 Before rotation, most Q06
1
,800
2 3 4
Q18
Q07
,701
,685
Qs loaded highly on Q18 ,684
Q16 ,679 the first extracted Q13 ,647
Q13 ,673 factor and much lower Q07
Q14
,638
,579
Q12 ,669 on the following ones. Q10 ,550
Q21 ,658
Q15 ,459
Q14 ,656
Q20 ,677
Q11 ,652 -,400 After rotation, all 4 Q21 ,661
Q17 ,643
Q04 ,634
extracted factors have Q03 -,567
Q03 -,629 a couple of Qs loading Q12 ,473 ,523
Q04
Q15 ,593 highly on them. Q16
,516
,514
Q01 ,586
Q01 ,496
Q05 ,556
Q05 ,429
Q08 ,549 ,401 -,417
Q08 ,833
Q10 ,437
Q12 loads equally Q17 ,747
Q20 ,436 -,404
Q19 -,427
high on factor 1 and 2! Q11 ,747
Q09 ,648
Q09 ,627
Q22 ,645
Q02
Q12: People try
,548
Q23 ,586
Q22 ,465
Q06 ,562 ,571 to tell you that Q02
Q19
,543
,427
Q23 ,507
SPSS makes Extraction Method: Principal Component Analysis.
Extraction Method: Principal Component Analysis.
a. 4 components extracted. statistics easier to Rotation Method: Varimax with Kaiser Normalization.
a. Rotation converged in 9 iterations.
understand but it
doesn't

34. Looking at the content of the Qs:
In order to interpret the factors, we have to
look at the content of the Qs that load highly
on them:
Factor 1: 'Fear of computers' Load
F1 F2 F3 F4
Q06 I have little experience of computers .800
Q18 SPSS always crashes when I try to use it .684
I worry that I will cause irreparable
damage because of my incompetence with
Q13 computers .647
Q7 All computers hate me .638
Computers have minds of their own and
Q14 deliberately go wrong whenever I use them .579
Computers are useful only for playing
Q10 games .550
Q15 Computers are out to get me .459

35. Looking at the content of the Qs:
Factor 2: 'Fear of statistics' Load
F1 F2 F3 F4
Q20 I can't sleep for thoughts of eigenvectors .677
I wake up under my duvet thinking that I
Q21 am trapped under a normal distribution .661
Q03 Standard deviations excite me -.567
People try to tell you that SPSS makes
statistics easier to understand but it
Q12 doesn't .473 .523
I dream that Pearson is attacking me with
Q04 correlation coefficients .516
I weep openly at the mention of central
Q16 tendency .514
Q01 Statistics makes me cry .496
Q05 I don't understand statistics .429

36. Looking at the content of the Qs:
Factor 3: 'Fear of mathematics' Load
F1 F2 F3 F4
Q08 I have never been good at mathematics .833
I slip into a coma whenever I see an
Q17 equation .747
Q11 I did badly at mathematics at school .747

37. Looking at the content of the Qs:
Factor 4: 'Peer evaluation' Load
F1 F2 F3 F4
Q09 My friends are better at statistics than me .648
Q22 My friends are better at SPSS than me .645
If I am good at statistics my friends will
Q23 think I'm a nerd .586
My frieds with think I'm stupid for not being
Q02 able to cope with SPSS .543
Q19 Everybody looks at me when I use SPSS .427

38. 4 subscales of the SAQ
Factor Subscale of SAQ
1 Fear of computers
2 Fear of statistics
3 Fear of mathematics
4 Fear of negative peer evalution
Now the question arises if
1. SAQ does not measure what it says ('SPSS anxiety') but
some related constructs
2. These four constructs are sub-components of SPSS anxiety.
The Factor Analysis does not tell us

39. Oblique rotation
While in orthogonal rotation, we have only one matrix,
the factor matrix, in oblique rotation the factor matrix is
split up into the pattern matrix and the structure matrix.
Pattern matrix Structure Matrix
contains the factor takes into account the
loadings and is relationship betweeen
interpreted like the factors
factor matrix.
should be used as a
is easier to interpret check on the pattern
should be reported matrix
should also be
reported

40. Oblique rotation – pattern matrix
The pattern matrix gives us the unique contribution
of a variable to a factor.
The same 4 patterns seem to have emerged
Pattern Matrixa
F1:
Component
1 2 3 4
Q20 I can't sleep for thoughts of eigen vectors ,706
Q21 I wake up under my duvet thinking that I am trapped under a normal
distribtion
,591 'Fear of statistics'
Q03 Standard deviations excite me -,511
Q04 I dream that Pearson is attacking me with correlation coefficients ,405
Q16 I weep openly at the mention of central tendency ,400
Q01 Statiscs makes me cry
Q05 I don't understand statistics
F2:
Q22 My friends are better at SPSS than I am
Q09 My friends are better at statistics than me
,643
,621
'Fear of peer
Q23 If I'm good at statistics my friends will think I'm a nerd
Q02 My friends will think I'm stupid for not being able to cope with SPSS
,615 evaluation'
,507
Q19 Everybody looks at me when I use SPSS
Q06 I have little experience of computers ,885
Q18 SPSS always crashes when I try to use it ,713
Q07 All computers hate me ,653
Q13 I worry that I will cause irreparable damage because of my
incompetenece with computers
,650 F3:
Q14 Computers have minds of their own and deliberately go wrong
whenever I use them
,588 'Fear of computers'
Q10 Computers are useful only for playing games ,585
Q12 People try to tell you that SPSS makes statistics easier to understand
,412 ,462
but it doesn't
Q15 Computers are out to get me
Q08 I have never been good at mathematics
,411
-,902
F4:
Q17 I slip into a coma whenever I see an equation
Q11 I did badly at mathematics at school
-,774
-,774
'Fear of mathematics'
Extraction Method: Principal Component Analysis.
Rotation Method: Oblimin with Kaiser Normalization.
a. Rotation converged in 29 iterations.

41. Oblique rotation – structure matrix
In the structure matrix, the shared variance is not ignored.
Now several variables load highly onto more than 1 factor.
Structure Matrix
1 2
Component
3 4
Factors 1 and 3
Q21 I wake up under my duvet thinking that I am trapped
under a normal distribtion
,695 ,477 'fear of statistics' and
Q20 I can't sleep for thoughts of eigen vectors ,685 'fear of computers'
go together.
Q03 Standard deviations excite me -,632 -,407
Q16 I weep openly at the mention of central tendency ,567 ,516 -,491
Q04 I dream that Pearson is attacking me with
correlation coefficients
,548 ,487 -,485 Also F4 'fear of math'
Q01 Statiscs makes me cry
Q05 I don't understand statistics
,520
,462
,413
,453
-,501
is related
Q22 My friends are better at SPSS than I am ,660
Q09 My friends are better at statistics than me ,653
Q23 If I'm good at statistics my friends will think I'm a
,588
nerd
Q02 My friends will think I'm stupid for not being able to
,546 Note: Factor 3 'fear of
cope with SPSS
computers' appears twice,
Q19 Everybody looks at me when I use SPSS -,435 ,446
Q06 I have little experience of computers ,777
each time together with a
Q18 SPSS always crashes when I try to use it ,404 ,761
different factor
Q07 All computers hate me ,401 ,723
Q13 I worry that I will cause irreparable damage
because of my incompetenece with computers ,723 -,429
Q14 Computers have minds of their own and
,426 ,671
deliberately go wrong whenever I use them
Q12 People try to tell you that SPSS makes statistics
,576 ,606
Factors 3 and 4
easier to understand but it doesn't
Q15 Computers are out to get me ,561 -,441 'fear of computers'
Q10 Computers are useful only for playing games
Q08 I have never been good at mathematics
,556
-,855 and 'fear of math'
Q17 I slip into a coma whenever I see an equation
Q11 I did badly at mathematics at school
,453
,451
-,822
-,818
go together
Extraction Method: Principal Component Analysis.
Rotation Method: Oblimin with Kaiser Normalization.

42. Oblique rotation: Component correlation matrix
The Component Correlation matrix contains the
correlation coefficients between factors.
F2 'fear of peer evaluation' has little relation
with the others, but F1,3,4 'fear of stats, computers,
and maths', are somewhat interrelated.
Component Correlation Matrix
Component 1 2 3 4
1 1,000 -,154 ,364 -,279
2 -,154 1,000 -,185 8,155E-02
3 ,364 -,185 1,000 -,464
4 -,279 8,155E-02 -,464 1,000
Extraction Method: Principal Component Analysis.
Rotation Method: Oblimin with Kaiser Normalization.
Independence of factors cannot be upheld, given the correlations between the factors and
also the content of the factors: 'fear of stats, computers, and maths's, all have a similar
meaning. oblique rotation is more sensible.

43. Factors – statistically and conceptually
The Factor Analysis has extracted 4 factors, 3 of which are correlated
with each other, one of which is rather independent. An oblique rotation
is more sensible given the interrelation between 3 factors.
How does that match the interpretation of the factors?
The three correlated factors
– fear of stats – fear of math – fear of computers
are also conceptually closely related whereas the
4th factor 'fear of negative peer evaluation', being socially based, is also
conceptually different.
Hence, the statistics and the meaning of the factors go along with each
other rather nicely.

44. Interim summary
SAQ has 4 factors underlyingly, which we can identify as
fear of
– stats – maths – computers – peer evaluation
Oblique rotation is to be preferred since three of the four
factors are inter-related, statistically as well as conceptually
The use of Factor Analysis here is purely exploratory. It
helps you understand what factors are underlying large
data sets
Informed decisions may follow from such an exploratory
Factor Analysis, e.g., wrt working out a better
questionnaire.