The document discusses research methods in psychology, including:
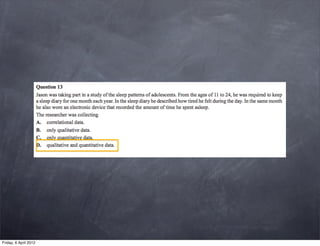
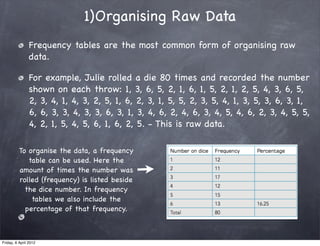
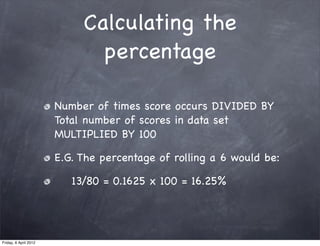
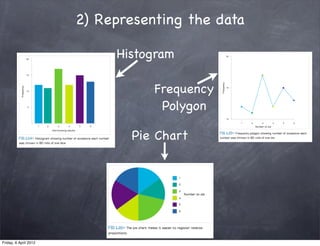
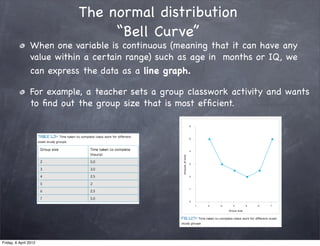
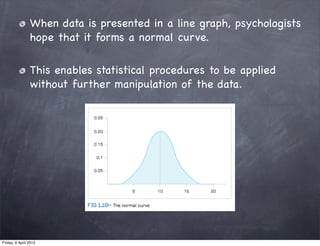
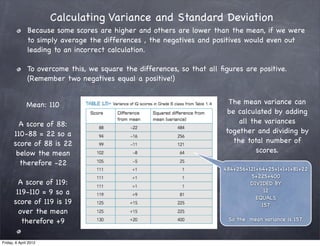
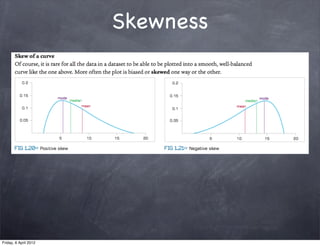
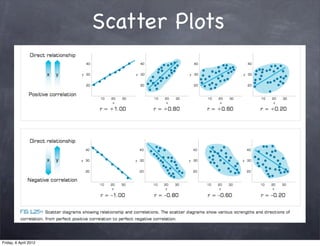
1) Descriptive statistics such as measures of central tendency (mean, median, mode), variability (range, variance, standard deviation), and organizing data in tables and graphs.
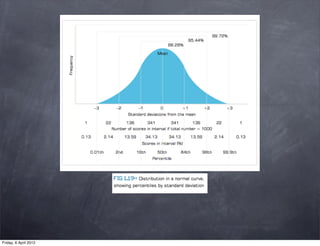
2) Inferential statistics and p-values, which are used to determine if differences or variations from the mean are statistically significant or likely due to chance.
3) The importance of generalizing results to populations and criteria for doing so, such as statistical significance at p<0.05 and controlling for confounding variables.