This document discusses group theory concepts including:
1) Definitions of groups, abelian groups, order of groups and elements.
2) Properties of cyclic groups, including examples like Zn and Z.
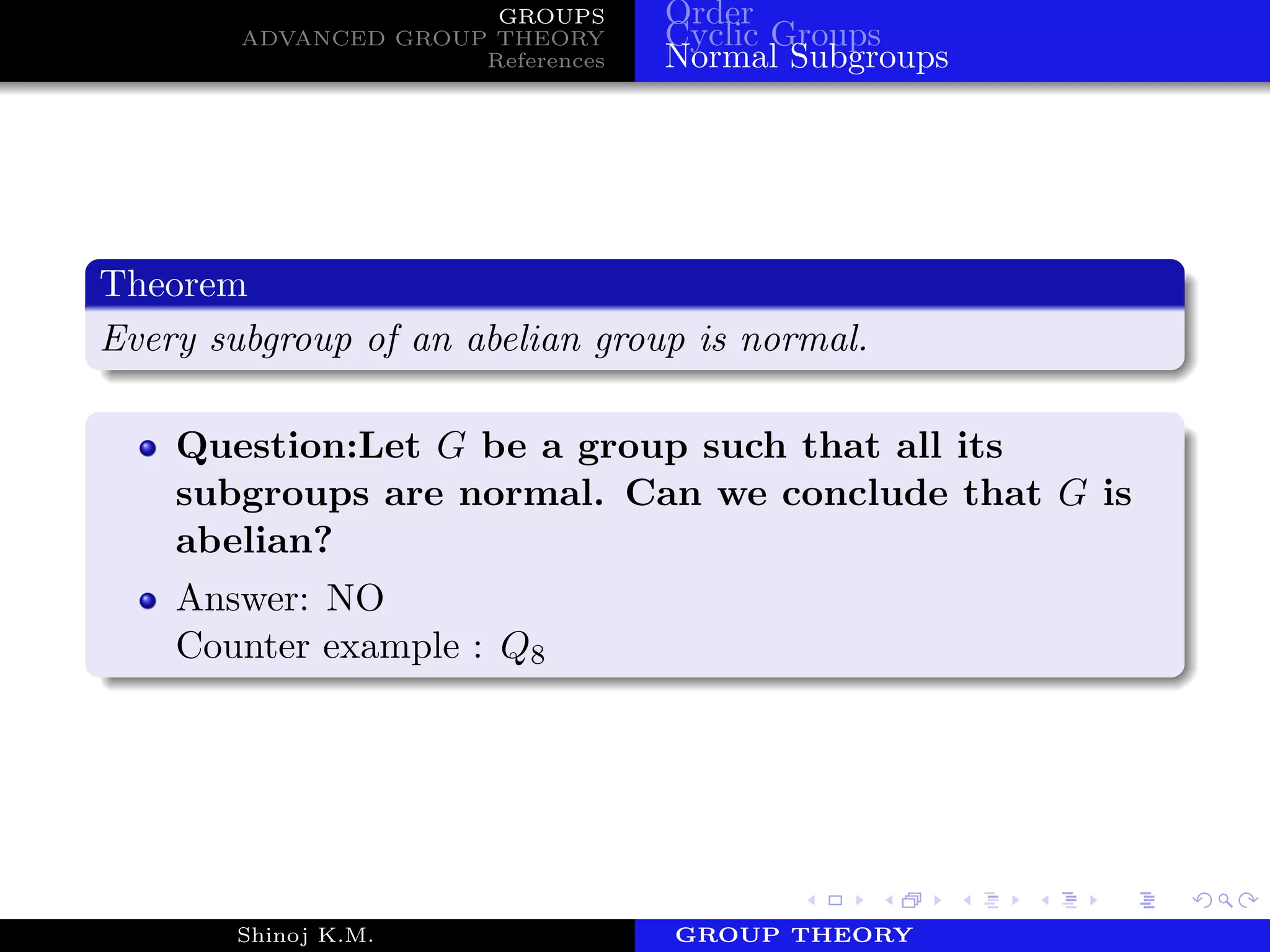
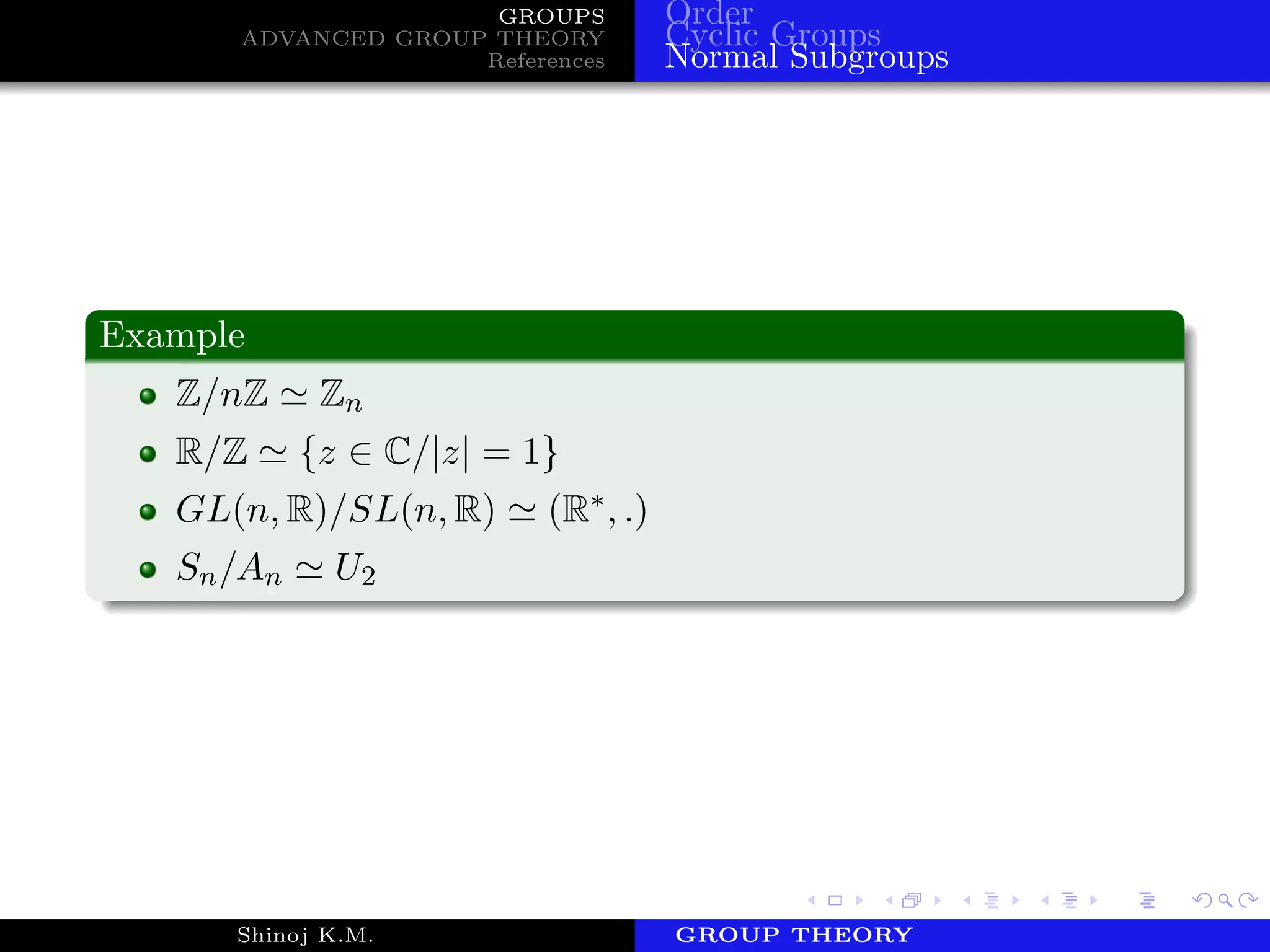
3) Introduction to normal subgroups and their properties. Factor groups and homomorphisms are also discussed.







































![GROUPS
ADVANCED GROUP THEORY
References
REFERENCES
[1] Joseph A. Gallian ,”Contemporary Abstract Algebra” ,
Narosa Publishing House.
[2] John.B.Fraleigh, ”A First Course in Abstract Algebra”.
[3] Thomas V.Hungerford, ”Abstract Algebra”
Shinoj K.M. Department of MathematicsGROUP THEORY](https://image.slidesharecdn.com/mokerialgebrapsn-191214090638/75/Group-Theory-42-2048.jpg)
