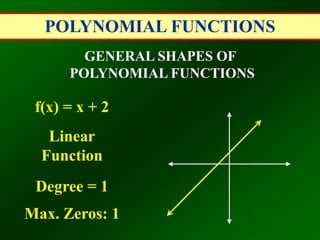
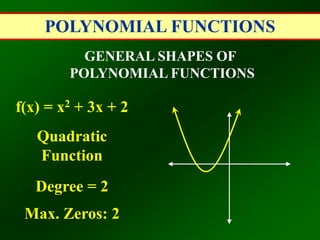
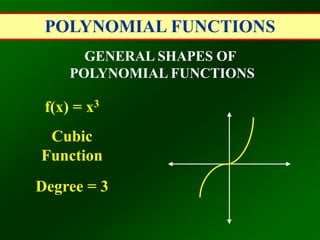
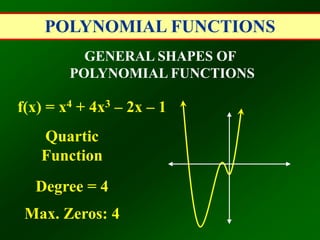
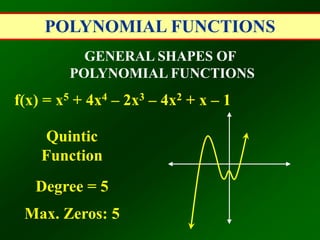
This document defines and explains polynomial functions. A polynomial is the sum of monomials, which are terms with variables raised to whole number exponents. The degree of a polynomial is the highest exponent of the variable. The leading coefficient is the coefficient of the term with the highest degree. Polynomial functions are classified based on degree as linear, quadratic, cubic, etc. and their general shapes depend on the degree and number of possible zeros. The end behavior of a polynomial function as x approaches positive or negative infinity depends on whether the degree is even or odd and if the leading coefficient is positive or negative.

1. POLYNOMIAL FUNCTIONS
A POLYNOMIAL is a monomial
or a sum of monomials.
A POLYNOMIAL IN ONE
VARIABLE is a polynomial that
contains only one variable.
Example: 5x2 + 3x - 7

2. POLYNOMIAL FUNCTIONS
The DEGREE of a polynomial in one variable is
the greatest exponent of its variable.
A LEADING COEFFICIENT is the coefficient
of the term with the highest degree.
What is the degree and leading
coefficient of 3x5 – 3x + 2 ?

3. POLYNOMIAL FUNCTIONS
A polynomial equation used to represent a
function is called a POLYNOMIAL FUNCTION.
Polynomial functions with a degree of 1 are called
LINEAR POLYNOMIAL FUNCTIONS
Polynomial functions with a degree of 2 are called
QUADRATIC POLYNOMIAL FUNCTIONS
Polynomial functions with a degree of 3 are called
CUBIC POLYNOMIAL FUNCTIONS

4. POLYNOMIAL FUNCTIONS
EVALUATING A POLYNOMIAL FUNCTION
Find f(-2) if f(x) = 3x2 – 2x – 6
f(-2) = 3(-2)2 – 2(-2) – 6
f(-2) = 12 + 4 – 6
f(-2) = 10

5. POLYNOMIAL FUNCTIONS
EVALUATING A POLYNOMIAL FUNCTION
Find f(2a) if f(x) = 3x2 – 2x – 6
f(2a) = 3(2a)2 – 2(2a) – 6
f(2a) = 12a2 – 4a – 6

6. POLYNOMIAL FUNCTIONS
GENERAL SHAPES OF
POLYNOMIAL FUNCTIONS
f(x) = 3
Constant
Function
Degree = 0
Max. Zeros: 0

7. POLYNOMIAL FUNCTIONS
GENERAL SHAPES OF
POLYNOMIAL FUNCTIONS
f(x) = x + 2
Linear
Function
Degree = 1
Max. Zeros: 1

8. POLYNOMIAL FUNCTIONS
GENERAL SHAPES OF
POLYNOMIAL FUNCTIONS
f(x) = x2 + 3x + 2
Quadratic
Function
Degree = 2
Max. Zeros: 2

9. POLYNOMIAL FUNCTIONS
GENERAL SHAPES OF
POLYNOMIAL FUNCTIONS
f(x) = x3
Cubic
Function
Degree = 3

10. POLYNOMIAL FUNCTIONS
GENERAL SHAPES OF
POLYNOMIAL FUNCTIONS
f(x) = x4 + 4x3 – 2x – 1
Quartic
Function
Degree = 4
Max. Zeros: 4

11. POLYNOMIAL FUNCTIONS
GENERAL SHAPES OF
POLYNOMIAL FUNCTIONS
f(x) = x5 + 4x4 – 2x3 – 4x2 + x – 1
Quintic
Function
Degree = 5
Max. Zeros: 5

12. POLYNOMIAL FUNCTIONS
END BEHAVIOR
Degree: Even
Leading Coefficient: +
End Behavior:
As x  -∞; f(x)  +∞
As x  +∞; f(x)  +∞
f(x) = x2

13. POLYNOMIAL FUNCTIONS
END BEHAVIOR
Degree: Even
Leading Coefficient: –
End Behavior:
As x  -∞; f(x)  -∞
As x  +∞; f(x)  -∞
f(x) = -x2

14. POLYNOMIAL FUNCTIONS
END BEHAVIOR
Degree: Odd
Leading Coefficient: +
End Behavior:
As x  -∞; f(x)  -∞
As x  +∞; f(x)  +∞
f(x) = x3

15. POLYNOMIAL FUNCTIONS
END BEHAVIOR
Degree: Odd
Leading Coefficient: –
End Behavior:
As x  -∞; f(x)  +∞
As x  +∞; f(x)  -∞
f(x) = -x3