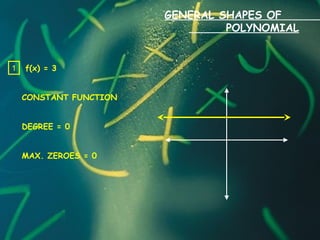
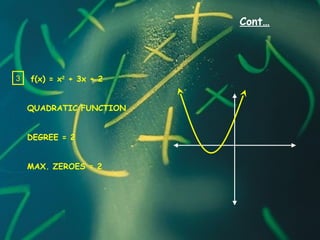
The document provides information about polynomials including: 1) A polynomial is an expression constructed from variables and constants using operations of addition, subtraction, multiplication, and exponents. 2) The degree of a polynomial refers to the exponent of its highest term. For example, a quadratic polynomial is degree 2 and a cubic is degree 3. 3) The zeros of a polynomial are the values that make the polynomial equal to 0. Finding the zeros involves solving the polynomial equation. 4) The relationships between the zeros and coefficients of a polynomial can be used to find unknown coefficients or zeros.

1. Submitted By:-
Anshul Chauhan of Class xth

2. Polynomials
2x2 + 3x = 5
2x2 + 3x= 9
x3
– 3x2
+ x +1 = 0 4y
3 - 4y
2 + 5y + 8 = 0
9x2
+ 9y + 8 =0

3. Introduction :
A polynomial is an expression of finite length
constructed from
variables and constants, using only the operations of
addition,
subtraction, multiplication, and non-negative, whole-
number exponents.
Polynomials appear in a wide variety.

4. Let x be a variable n, be a positive integer
and as, a1,a2,….an be constants (real nos.)
Then, f(x) = anxn
+ an-1xn-1
+….+a1x+xo
 anxn
,an-1xn-1
,….a1x and ao are known as the
terms of the polynomial.
 an,an-1,an-2,….a1 and ao are their coefficients.
For example:
• p(x) = 3x – 2 is a polynomial in variable x.
• q(x) = 3y2
– 2y + 4 is a polynomial in variable y.
• f(u) = 1/2u3
– 3u2
+ 2u – 4 is a polynomial in variable u.
NOTENOTE: 2x2
– 3√x + 5, 1/x2
– 2x +5 , 2x3
– 3/x +4 are not polynomials.
Cont…

5. The exponent of the highest degree term in a polynomial is known
as its
degree.
For example:
 f(x) = 3x + ½ is a polynomial in the
variable x of degree 1.
 g(y) = 2y2
– 3/2y + 7 is a polynomial in
the variable y of degree 2.
 p(x) = 5x3
– 3x2
+ x – 1/√2 is a polynomial
in the variable x of degree 3.
 q(u) = 9u5
– 2/3u4
+ u2
– ½ is a polynomial
in the variable u of degree 5.
Degree of polynomial

6. Constant
polynomial:
For example:
f(x) = 7, g(x) = -3/2, h(x) = 2
are constant polynomials.
The degree of constant polynomials is not defined.

7. Linear polynomial:
For example:
 p(x) = 4x – 3, q(x) = 3y are linear polynomials.
Any linear polynomial is in the form ax + b, where a, b are
real
nos. and a ≠ 0.
It may be a monomial or a binomial. F(x) = 2x – 3 is binomial
whereas
g (x) = 7x is monomial.

8. Types of
polynomial:
 A polynomial of degree two is
called a quadratic polynomial.
 f(x) = √3x2
– 4/3x + ½, q(w)
= 2/3w2
+ 4 are quadratic
polynomials with real
coefficients.
Any quadratic is always in the
form f(x) = ax2
+ bx +c where
a,b,c are real nos. and a ≠ 0.
 A polynomial of degree
three is called a cubic
polynomial.
 f(x) = 9/5x3
– 2x2
+ 7/3x
_1/5 is a cubic polynomial in
variable x.
Any cubic polynomial is
always in the form f(x = ax3
+ bx2 +cx + d where a,b,c,d
are real nos.

9. Value’s & zero’s of
Polynomial
A real no. x is a zero of
the polynomial f(x),is f(x) =
0
Finding a zero of the
polynomial means solving
polynomial equation f(x) = 0.
If f(x) is a polynomial and
y is any real no. then real
no. obtained by replacing x
by y in f(x) is called the
value of f(x) at x = y and
is denoted by f(x).
Value of f(x) at x = 1
f(x) = 2x2
– 3x – 2
 f(1) = 2(1)2
– 3 x 1 – 2
= 2 – 3 – 2
= -3
Zero of the polynomial
f(x) = x2
+ 7x +12
 f(x) = 0
x2 + 7x + 12 = 0
(x + 4) (x + 3) = 0
x + 4 = 0 or, x + 3 = 0
x = -4 , -3

10. GRAPHS
OF
THE
POLYNOMIALS
GRAPHS
OF
THE
POLYNOMIALS

11. GENERAL SHAPES OF
POLYNOMIAL
f(x) = 3
CONSTANT FUNCTION
DEGREE = 0
MAX. ZEROES = 0
1

12. Cont….
f(x) = x + 2
LINEAR FUNCTION
DEGREE =1
MAX. ZEROES = 1
2

13. Cont…
f(x) = x2
+ 3x + 2
QUADRATIC FUNCTION
DEGREE = 2
MAX. ZEROES = 2
3

14. Cont…
f(x) = x3
+ 4x2
+ 2
CUBIC FUNCTION
DEGREE = 3
MAX. ZEROES = 3
4

16. QUADRATICQUADRATIC
☻ α + β = - coefficient of x
Coefficient of x2
= - b
a
☻ αβ = constant term
Coefficient of x2
= c
a

17. CUBICCUBIC
 α + β + γ = -Coefficient of x2 =
-b
Coefficient of x3
a
 αβ + βγ + γα = Coefficient of x = c
Coefficient of x3
a
 αβγ = - Constant term = d
Coefficient of x3
a

18. Relationships
 ON VERYFYING THE
RELATIONSHIP BETWEEN
THE ZEROES AND
COEFFICIENTS
 ON FINDING THE
VALUES OF EXPRESSIONS
INVOLVING ZEROES OF
QUADRATIC POLYNOMIAL
 ON FINDING AN
UNKNOWN WHEN A
RELATION BETWEEEN
ZEROES AND COEFFICIENTS
ARE GIVEN.
 OF ITS
A
QUADRATIC
POLYNOMIAL WHEN
THE SUM
AND
PRODUCT OF ITS
ZEROES ARE GIVEN.

20. If f(x) and g(x) are any two
polynomials with g(x) ≠
0,then we can always find
polynomials q(x), and r(x)
such that :
F(x) = q(x) g(x) + r(x),F(x) = q(x) g(x) + r(x),
Where r(x) = 0 or degree
r(x) < degree g(x)
 ON VERYFYING THE
DIVISION ALGORITHM
FOR POLYNOMIALS.
ON FINDING THE
QUOTIENT AND
REMAINDER USING
DIVISION ALGORITHM.
ON CHECKING WHETHER A
GIVEN POLYNOMIAL IS A
FACTOR OF THE OTHER
POLYNIMIAL BY APPLYING
THEDIVISION ALGORITHM
ON FINDING THE
REMAINING ZEROES OF A
POLYNOMIAL WHEN SOME OF
ITS ZEROES ARE GIVEN.

21. THANKS
FOR BEING
PATIENT