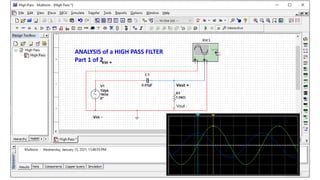
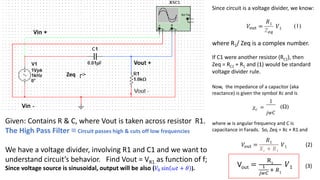
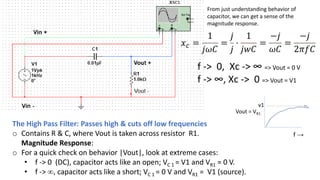
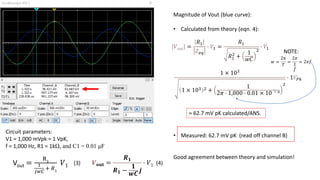
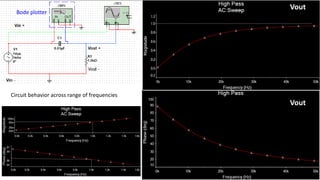
The document analyzes a high pass filter circuit consisting of a resistor and capacitor, detailing the circuit's voltage response across varying frequencies. It highlights how the circuit passes high frequencies while cutting off low frequencies, using mathematical and graphical representations. Measurement data from an oscilloscope confirms the theoretical predictions regarding the output voltage and phase relationships with a sinusoidal input.

1. ANALYSIS of a HIGH PASS FILTER
Part 1 of 2

2. Given: Contains R & C, where Vout is taken across resistor R1.
The High Pass Filter ≡ Circuit passes high & cuts off low frequencies
We have a voltage divider, involving R1 and C1 and we want to
understand circuit’s behavior. Find Vout = VR1 as function of f;
Since voltage source is sinusoidal, output will be also (𝑉0 sin 𝜔𝑡 + 𝜃 ).
Since circuit is a voltage divider, we know:
𝑉out =
𝑅1
𝑍𝑒𝑞
𝑉1
where R1/ Zeq is a complex number.
If C1 were another resistor (RC1), then
Zeq = RC1 + R1 and (1) would be standard
voltage divider rule.
Now, the impedance of a capacitor (aka
reactance) is given the symbol Xc and is
𝜒𝑐 =
1
𝑗𝑤𝐶
where w is angular frequency and C is
capacitance in Farads. So, Zeq = Xc + R1 and
𝑉out =
𝑅1
𝑋𝑐 + 𝑅1
𝑉1
Vout =
R1
1
𝑗𝑤𝐶
+ 𝑅1
𝑉1
Zeq ┌>
(Ω)
(1)
(2)
(3)

3. The High Pass Filter: Passes high & cuts off low frequencies
o Contains R & C, where Vout is taken across resistor R1.
Magnitude Response:
o For a quick check on behavior |Vout|, look at extreme cases:
• f -> 0 (DC), capacitor acts like an open; VC 1 = V1 and VR1 = 0 V.
• f -> ∞, capacitor acts like a short; VC 1 = 0 V and VR1 = V1 (source).
𝑥𝑐 =
1
𝑗𝜔𝐶
=
𝑗
𝑗
⋅
1
𝑗𝑤𝐶
=
−𝑗
𝜔𝐶
=
−𝑗
2𝜋𝑓𝐶
f -> 0, Xc -> ∞ => Vout = 0 V
f -> ∞, Xc -> 0 => Vout = V1
Vout = VR1
f →
v1
From just understanding behavior of
capacitor, we can get a sense of the
magnitude response.

4. The High Pass Filter: Passes high & cuts off low frequencies
Phase Response
We can use phasor math to quickly analyze the phase behavior of Vout.
A phasor, 𝑧 = 𝑧 ∡𝜃, is another way to represent a complex number &
allows for quick calculation when multiplying and/or dividing.
𝑧𝑚 = 𝑧1𝑧2 = 𝑧1 ∡𝜃1 ∗ 𝑧2 ∡𝜃2 = 𝑧1 𝑧2 ∡ 𝜃1 + 𝜃2
𝑧𝐷 =
𝑧1
𝑧2
=
𝑧1 ∡𝜃1
𝑧2 ∡𝜃2
=
𝑧1
|𝑧2|
∡ 𝜃1 − 𝜃2
𝑅∡𝑜𝑜
𝑧𝑒𝑞 = |𝑧𝑒𝑞|∡ − 𝜃𝑒𝑞
Vout =
𝐑𝟏
𝟏
𝒋𝒘𝑪
+ 𝑹𝟏
𝑽𝟏
𝑧eq = 𝑅∡𝑂0 +
−𝑗
𝜔𝐶
= 𝑅 −
1
𝜔𝐶
𝑗 = 𝑧𝑒𝑞 ∡ − 𝜃𝑒𝑞
𝑉out =
𝑅1∡00
𝑧𝑒𝑞 ∡ − 𝜃𝑒𝑞
𝑉1∡00
𝑉out =
𝑅1
𝑧eq
∡0o
− −𝜃e𝑞
𝑜
𝑉1∡𝑂0
=
𝑅1
|𝑍𝑒𝑞|
∡𝜃e𝑞
𝑜
⋅ 𝑉1
V𝑜𝑢𝑡 ∡𝜃𝑒𝑞
This means that Vout leads V1!
𝑥𝑐 =
1
𝑗𝑤𝐶
=
−𝑗
𝑤𝐶
θeq
-θeq
(3)

5. ANALYSIS of a HIGH PASS FILTER
Part 2 of 2

6. Zeq ┌>
Let’s look at oscilloscope data for our circuit:
Channel A is connected to V1 our voltage source (green curve).
Our voltage source is listed at 1V peak. Channel A is scaled at
500 mV/Div; green curve covers 2 Div = 500 mV x 2 = 1 Vpk.
Channel B is connected to Vout (blue curve).
Vout leads V1 as predicted in last slide.
Note channel A & B do not have same voltage scale.
Circuit parameters:
V1 = 1,000 mVpk = 1 VpK,
f = 1,000 Hz, R1 = 1kΩ, and C1 = 0.01 μF

7. Circuit parameters:
V1 = 1,000 mVpk = 1 VpK,
f = 1,000 Hz, R1 = 1kΩ, and C1 = 0.01 μF
Vout =
R1
1
𝑗𝑤𝐶
+ 𝑅1
𝑉1 (3)
Magnitude of Vout (blue curve):
• Calculated from theory (eqn. 4):
• Measured: 62.7 mV pK (read off channel B)
Good agreement between theory and simulation!
𝑽𝐨𝐮𝐭 =
𝑹𝟏
𝑹𝟏 −
𝟏
𝒘𝑪
𝒋
⋅ 𝑉1 (4)
𝑉𝑜𝑢𝑡 =
𝑅1
𝑍𝑒𝑞
⋅ 𝑉1 =
𝑅1
𝑅1
2
+
1
𝑤𝐶
2
⋅ 𝑉1
1 × 103
1 × 103 2 +
1
2𝜋 ⋅ 1,000 ⋅ 0.01 × 10
− 6
2
⋅ 1𝑉𝑃𝑘
= 62.7 mV pK calculated/ANS.
-
𝑤 =
2𝜋
𝑇
=
2𝜋
1
𝑓
= 2𝜋𝑓
NOTE:

8. Circuit parameters:
V1 = 1,000 mVpk = 1 VpK,
f = 1,000 Hz, R1 = 1kΩ, and C1 = 0.01 μF
Vout =
R1
1
𝑗𝑤𝐶
+ 𝑅1
𝑉1 (3)
Phase of Vout (blue curve):
• Calculated from theory: Using phasors, we can
analyze equation (4) quickly.
Numerator is a real number whose value is R1. Real
numbers have a 0⁰ angle.
Denominator was left in cartesian coordinate form. To
find the angle we’ll use arctan Y/X.
𝑽𝐨𝐮𝐭 =
𝑹𝟏
𝑹𝟏 −
𝟏
𝒘𝑪
𝒋
⋅ 𝑉1 (4)
∡𝜃𝑑𝑒𝑛 = tan−1
𝑦
𝑥
= tan−1
−1
𝑤𝐶1
𝑅1
= tan−1
−1
𝜔𝑅1𝐶1
∡𝜃den = tan−1
−1
2𝜋 ⋅ 1000 ⋅ 1000 ⋅ 0.01 × 10
− 6
= −86.4⁰
∡𝜃𝑣0ut
= ∡𝜃𝑛𝑢𝑚 − ∡𝜃den = 0 − −86.40
= 86.4⁰
• Measured: ∡𝜃𝑉𝑜𝑢𝑡 = 𝜔𝑡 = 2𝜋𝑓𝑡
= 2𝜋 ⋅ 1000 ⋅ 238.64 × 1.0−6 ⋅
1800
Π
= 85.9
0

9. Vout
Vout
Bode plotter
Circuit behavior across range of frequencies