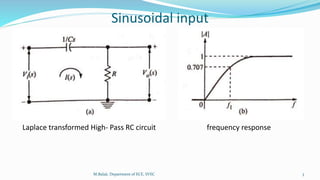
The document discusses high-pass RC circuits and their response to different input signals. It describes how a high-pass RC circuit only transmits high-frequency signals and attenuates low frequencies. The circuit's behavior depends on the relationship between the RC time constant and the input signal period. For a square wave input, if RC is much larger than the period, the output follows the input. If RC is comparable to the period, the output is exponentially charging and discharging. And if RC is much smaller, the output is nearly the same as the input.

1. Electronic Devices and Circuits
UNIT – I
SVEC19

2. The High-Pass RC Circuit
𝑋 𝐶 =
1
2𝜋𝑓𝐶
When f= 0; XC = ∞ (Capacitor is open
circuited);
Vo(t) = 0; then gain A=
𝑉𝑜(𝑡)
𝑉 𝑖(𝑡)
= 0.
When f increases, XC decreases, then
output and gain increases.
When f= ∞; XC = 0 (Capacitor is short
circuited);
M.Balaji, Department of ECE, SVEC 2
The circuit which transmits only high- frequency signals and attenuates or
stops low frequency signals.

3. Sinusoidal input
M.Balaji, Department of ECE, SVEC 3
Laplace transformed High- Pass RC circuit frequency response

4. 𝐴 =
𝑉𝑂 𝑠
𝑉𝑖 𝑠
=
𝑅
𝑅 +
1
𝐶𝑠
=
1
1 +
1
𝑅𝐶𝑠
Putting s= j 𝜔,
𝐴 =
1
1 − 𝑗
1
𝜔𝑅𝐶
=
1
1 − 𝑗
1
2𝜋𝑓𝑅𝐶
∴ 𝐴 =
1
1 +
1
2𝜋𝑓𝑅𝐶
2
𝑎𝑛𝑑 𝜃 = −𝑡𝑎𝑛−1
1
2𝜋𝑓𝑅𝐶
M.Balaji, Department of ECE, SVEC 4

5. M.Balaji, Department of ECE, SVEC 5
𝐴𝑡 𝑡ℎ𝑒 𝑙𝑜𝑤𝑒𝑟 𝑐𝑢𝑡𝑜𝑓𝑓 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑓1, 𝐴 =
1
2
1
1 +
1
2𝜋𝑓1 𝑅𝐶
2
=
1
2
Squaring on both sides and equating the denominators,
1
2𝜋𝑓1 𝑅𝐶
= 1
∴ 𝑓1 =
1
2𝜋𝑅𝐶

6. Step Voltage input
A step signal is one which maintains the value
zero for all times t < 0; and maintains the value
V for all times t > 0.
M.Balaji, Department of ECE, SVEC 6
t =
0
-
t =
0
+
t < 0 t > 0
t = 0
The transition between the two voltage
levels takes place at t = 0.
Vi = 0, immediately before t = 0 (to be
referred to as time t= 0-) and Vi = V,
immediately after t= 0 (to be referred to as
time t= 0+).

7. Step input
M.Balaji, Department of ECE, SVEC 7
Step input Step response for different time constants
𝑉0 𝑡 = 𝑉𝑓 − 𝑉𝑓 − 𝑉𝑖 𝑒− 𝑡 𝑅𝐶
V 𝑒− 𝑡 𝑅𝐶
When Vf = 0

8. Pulse input
 The pulse is equivalent to a positive step followed by a delayed negative step.
M.Balaji, Department of ECE, SVEC 8
Pulse waveform Pulse waveform in terms of step

9. M.Balaji, Department of ECE, SVEC 9
RC >> tp

10. M.Balaji, Department of ECE, SVEC 10
RC comparable to tp

11. M.Balaji, Department of ECE, SVEC 11
RC << tp

12. M.Balaji, Department of ECE, SVEC 12
(a) RC >> tp (b) RC comparable to tp (c) RC << tp

13. Square wave input
 A square wave is a periodic waveform which maintains itself at one constant
level V’ with respect to ground for a time T1, and then changes abruptly to
another level V’’, and remains constant at that level for a time T2, and repeats
itself at regular intervals of time T1+T2.
 A square wave may be treated as a series of positive and negative pulses.
M.Balaji, Department of ECE, SVEC 13

14. M.Balaji, Department of ECE, SVEC
14
(a) Square wave input (b) When RC is arbitrarily large

15. M.Balaji, Department of ECE, SVEC 15
(c) RC > T

16. M.Balaji, Department of ECE, SVEC 16
(d) Output when RC comparable to T

17. M.Balaji, Department of ECE, SVEC 17
(e) Output when RC << T

18. Under steady state conditions, the capacitor charges and discharges to the
same voltage levels in each cycle. So, the shape of the output waveform is
fixed.
𝑓𝑜𝑟 0 < 𝑡 < 𝑇1, the output is given by 𝑣01 = 𝑉1 𝑒−𝑡/𝑅𝐶
At t=T1 ; 𝑣01 = 𝑉1 𝑒−𝑇1
/𝑅𝐶
𝑓𝑜𝑟 𝑇1 < 𝑡 < 𝑇1 + 𝑇2, the output is given by 𝑣02 = 𝑉2 𝑒−(𝑡−𝑇1
)/𝑅𝐶
At t=T1 +T2, 𝑣02 = 𝑉2 𝑒−𝑇2
/𝑅𝐶
Also 𝑉1
′
− 𝑉2 = 𝑉 𝑎𝑛𝑑 𝑉1 − 𝑉2
′
= 𝑉
M.Balaji, Department of ECE, SVEC 18

19. Expression for the percentage tilt
The expression for the percentage tilt can be derived when the time constant RC
of the circuit is very large compared to the period of the input waveform, i.e RC
>> T.
For a symmetrical square wave with zero average value
𝑉1 = −𝑉2, 𝑖. 𝑒 𝑉1 = 𝑉2
𝑉1
′
= −𝑉2
′
, 𝑖. 𝑒 𝑉1
′
= 𝑉2
′
𝑇1 = −𝑇2 =
𝑇
2
M.Balaji, Department of ECE, SVEC 19

20. The output waveform for RC >> T is
M.Balaji, Department of ECE, SVEC 20

21. 𝑉1
′
= 𝑉1 𝑒− 𝑇 2𝑅𝐶 𝑎𝑛𝑑 𝑉2
′
= 𝑉2 𝑒− 𝑇 2𝑅𝐶
𝑉1 − 𝑉2
′
= 𝑉
𝑉1 − 𝑉2 𝑒− 𝑇 2𝑅𝐶
= 𝑉1 + 𝑉1 𝑒− 𝑇 2𝑅𝐶
= 𝑉
𝑉1 =
𝑉
1 + 𝑒− 𝑇 2𝑅𝐶
𝑉 = 𝑉1(1 + 𝑒− 𝑇 2𝑅𝐶)
% 𝑇𝑖𝑙𝑡, 𝑃 =
𝑉1 − 𝑉1
′
𝑉
2
× 100
=
𝑉1 − 𝑉1 𝑒− 𝑇 2𝑅𝐶
𝑉1(1 + 𝑒− 𝑇 2𝑅𝐶)
× 200%
=
1 − 𝑒− 𝑇 2𝑅𝐶
1 + 𝑒− 𝑇 2𝑅𝐶
× 200%
M.Balaji, Department of ECE, SVEC 21

22. When the time constant is very large, i.e,
𝑇
𝑅𝐶
≪ 1
𝑃 =
1 − 1 +
−𝑇
2𝑅𝐶
+ (
−𝑇
2𝑅𝐶
)2 1
2!
+ ⋯
1 + 1 +
−𝑇
2𝑅𝐶
+ (
−𝑇
2𝑅𝐶
)2 1
2!
+ ⋯
× 200%
=
𝑇
2𝑅𝐶
2
× 200%
=
𝑇
2𝑅𝐶
× 100%
𝜋𝑓1
𝑓
× 100%
Where 𝑓1 =
1
2𝜋𝑅𝐶
𝑖𝑠 𝑡ℎ𝑒 𝑙𝑜𝑤𝑒𝑟 𝑐𝑢𝑡 − 𝑜𝑓𝑓 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 ℎ𝑖𝑔ℎ − 𝑝𝑎𝑠𝑠 𝑐𝑖𝑟𝑐𝑢𝑖𝑡
M.Balaji, Department of ECE, SVEC 22

23. Ramp input
M.Balaji, Department of ECE, SVEC 23
When a high- pass RC circuit is excited with a ramp input, i.e 𝑣𝑖 𝑡 = 𝛼𝑡,
𝑤ℎ𝑒𝑟𝑒 𝛼 is the slope of the ramp
then, 𝑉𝑖 𝑠 =
𝛼
𝑠2
From the Laplace transformed high-pass circuit, we get
𝑉0 𝑠 = 𝑉𝑖 𝑠
𝑅
𝑅 +
1
𝐶𝑠
=
𝛼
𝑠2
𝑅𝐶𝑠
1 + 𝑅𝐶𝑠
=
𝛼
𝑠(𝑠 +
1
𝑅𝐶
)
𝛼𝑅𝐶
1
𝑠
−
1
𝑠 +
1
𝑅𝐶

24. Taking inverse Laplace transform on both sides, we get
𝑉0 𝑡 = 𝛼𝑅𝐶 1 − 𝑒− 𝑡 𝑅𝐶
For time t which are very small in comparison with RC, we have
𝑉0 𝑡 = 𝛼𝑅𝐶 1 − 1 +
−𝑡
𝑅𝐶
+
−𝑡
𝑅𝐶
2 1
2!
+
−𝑡
𝑅𝐶
3 1
3!
+ ⋯
= 𝛼𝑅𝐶
𝑡
𝑅𝐶
−
𝑡2
2(𝑅𝐶)2
+ ⋯
= 𝛼𝑡 −
𝛼𝑡2
2𝑅𝐶
= 𝛼𝑡 1 −
𝑡
2𝑅𝐶
M.Balaji, Department of ECE, SVEC 24

25. M.Balaji, Department of ECE, SVEC 25
The above figures shows the response of the high-pass circuit for a ramp
input when (a) RC >> T and (b) RC << T, where T is the duration of the
ramp.
For small values of T, the output signal falls away slightly from the
input.

26. High-Pass RC circuit as a differentiator
 Sometimes, a square wave may need to be converted into
sharp positive and negative spikes (pulses of short
duration).
 By eliminating the positive spikes, we can generate a train
of negative spikes and vice-versa.
 The pulses so generated may be used to trigger a
multivibrator.
 If in a circuit, the output is a differential of the input
signal, then the circuit is called a differentiator.
M.Balaji, Department of ECE, SVEC 26

27. 𝜏 = 𝑅𝐶 ≪ 𝑇 then the circuit works as a differentiator
1/f ; here frequency must be small.
At low frequencies, 𝑋𝑐 =
1
2𝜋𝑓𝐶
= 𝑙𝑎𝑟𝑔𝑒 𝑤ℎ𝑒𝑛 𝑐𝑜𝑚𝑝𝑎𝑟𝑒𝑑 𝑡𝑜 𝑅
The voltage drop across R is very small when compared to the drop across C.
𝑉𝑖 =
1
𝐶
𝑖(𝑡) 𝑑𝑡 + 𝑖 𝑡 𝑅
𝑉𝑖 =
1
𝐶
𝑖(𝑡) 𝑑𝑡
𝑉𝑖 =
1
𝑅𝐶
𝑉0 𝑑𝑡 (𝑖 𝑡 =
𝑉0
𝑅
)
Differentiating on both sides we get
𝑑𝑉𝑖
𝑑𝑡
=
1
𝑅𝐶
𝑉0
𝑉0 = 𝑅𝐶
𝑑𝑉𝑖
𝑑𝑡
Thus , the output is proportional to the derivative of the input.
M.Balaji, Department of ECE, SVEC 27
V0 is small

28. Numerical Problem 1
A 1KHz symmetrical square wave of ±10𝑉 is applied to an RC circuit having 1ms
time constant. Calculate and plot the output for the RC configuration as a High-
Pass RC circuit.
Solution: Given 𝑓 = 1𝐾𝐻𝑧, 𝑇 = 1𝑚𝑠
∴ 𝑇𝑂𝑁 = 0.5𝑚𝑠 𝑎𝑛𝑑 𝑇𝑂𝐹𝐹 = 0.5𝑚𝑠 𝑑𝑢𝑒 𝑡𝑜 𝑠𝑦𝑚𝑚𝑒𝑡𝑟𝑖𝑐𝑎𝑙 𝑠𝑞𝑢𝑎𝑟𝑒 𝑤𝑎𝑣𝑒
𝜏 = 𝑅𝐶 = 1𝑚𝑠
Peak-to –peak amplitude VPP = 10- (-10)=20V
Since RC is comparable to T, the capacitor charges and discharges exponentially.
M.Balaji, Department of ECE, SVEC 28

29. High-Pass RC circuit
M.Balaji, Department of ECE, SVEC 29

30. When the 1 KHz square wave shown by dotted line is applied to the RC high
pass circuit.
Under steady state conditions the output waveform will be as shown by the
thick line.
Since the input signal is a symmetrical square wave, we have
𝑉1 = −𝑉2 𝑎𝑛𝑑 𝑉1
′
= −𝑉2
′
𝑉1
′
= 𝑉1 𝑒− 𝑇 2𝑅𝐶 = 𝑉1 𝑒−0.5 1 = 0.6065 𝑉1
𝑉2
′
= 𝑉2 𝑒− 𝑇 2𝑅𝐶 = 𝑉2 𝑒−0.5 1 = 0.6065 𝑉2
M.Balaji, Department of ECE, SVEC 30

31. 𝑉1
′
− (−𝑉2) = 20
0.6065 𝑉1 + 𝑉1 = 20
∴ 𝑉1 =
20
1.6065
= 12.449𝑉
𝑉2 = −𝑉1 = −12.449𝑉
𝑉1
′
= 20 − 𝑉1 = 20 − 12.449 = 7.551𝑉
𝑉2
′
= −𝑉1
′
= −7.551 𝑉
M.Balaji, Department of ECE, SVEC 31

32. Numerical Problem 2
If a square wave of 5 KHz is applied to an RC high-pass circuit and the resultant
waveform measured on a CRO was tilted from 15V to 10V, find out the lower 3-
dB frequency of the high-pass circuit.
Sol: f= 5 KHz
𝑉1= 15V
𝑉1
′
= 10𝑉
𝑓1 = ? 𝑙𝑜𝑤𝑒𝑟 3 𝑑𝐵 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦
M.Balaji, Department of ECE, SVEC 32

33. Peak-to-peak value of input 𝑉 = 𝑉1 + 𝑉2
= 15 + 15 = 30𝑉
𝑃 =
𝑉1 − 𝑉1
′
2
× 100
=
15 − 10
2
× 100 = 33.33%
Also% tilt 𝑃 =
𝜋𝑓1
𝑓
× 100
33.33 =
3.14𝑓1
5 × 103
× 100
𝑓1 =
33.33 × 5 × 103
3.14 × 100
= 530.56𝐻𝑧
M.Balaji, Department of ECE, SVEC 33