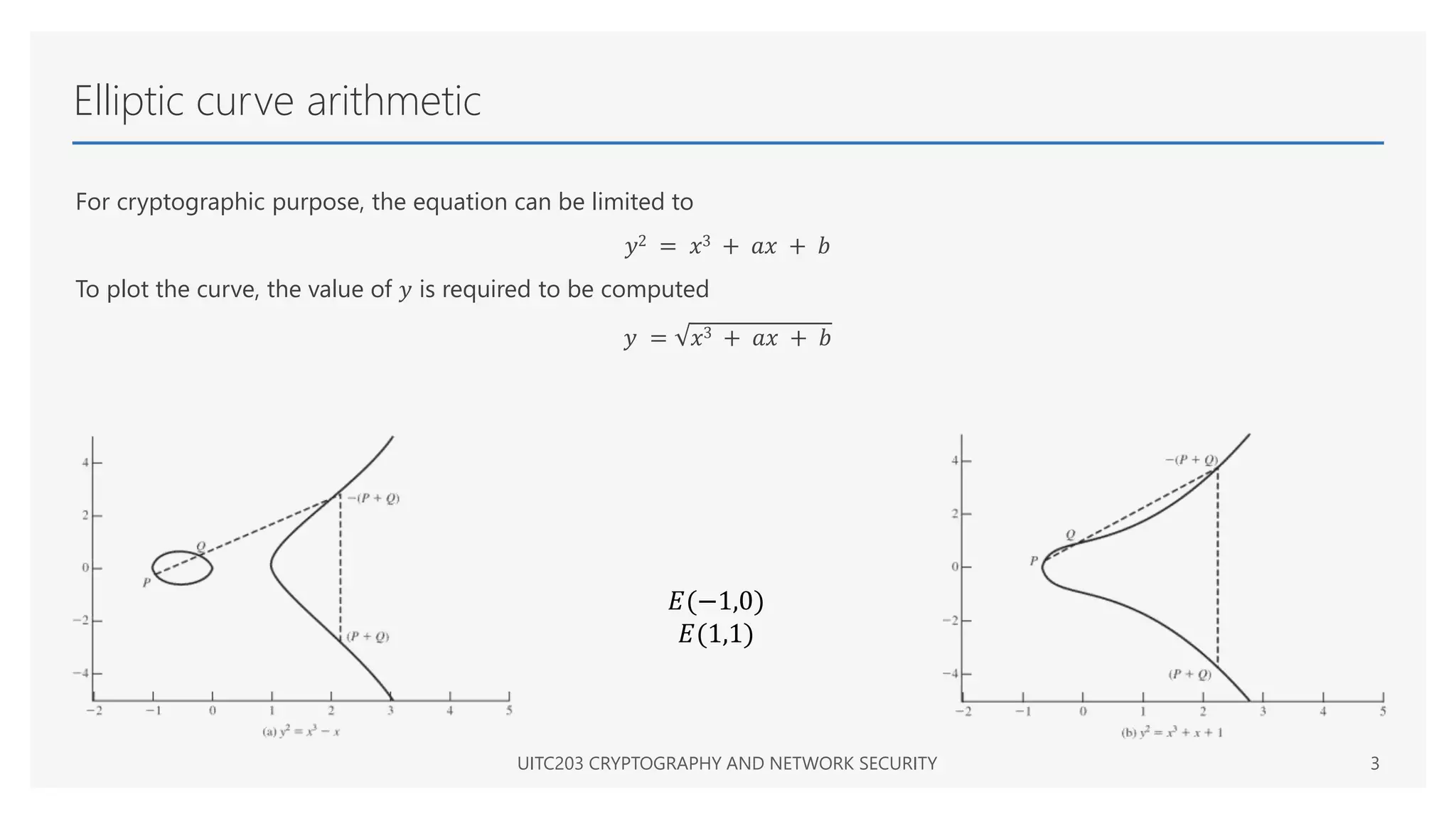
The document provides an overview of elliptic curve cryptography, detailing its mathematical foundation using Weierstrass equations and geometric interpretation of elliptic curve arithmetic. It describes the addition of points on elliptic curves and outlines two families of elliptic curves utilized in cryptographic applications: prime curves and binary curves. Additionally, it explains key generation and the Diffie-Hellman key exchange mechanism based on elliptic curves.

1. Elliptic Curve Cryptography
Adri Jovin J J, M.Tech., Ph.D.
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY

2. Introduction
• Introduced by Neal Koblitz and V. S. Miller
• An elliptic curve is defined by an equation in two variables with coefficients
• The variables and coefficients are restricted to elements in a finite field
• Elliptic curves are not ellipses, but called so since they are described by cubic equations
• Cubic equations for elliptic equations take the following form known as Weierstrass equation
𝑦2 + 𝑎𝑥𝑦 + 𝑏𝑦 = 𝑥3 + 𝑐𝑥2 + 𝑑𝑥 + 𝑒
where 𝑎, 𝑏, 𝑐, 𝑑, 𝑒 are real numbers and 𝑥, 𝑦 take values in real numbers
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY 2

3. Elliptic curve arithmetic
For cryptographic purpose, the equation can be limited to
𝑦2 = 𝑥3 + 𝑎𝑥 + 𝑏
To plot the curve, the value of 𝑦 is required to be computed
𝑦 = 𝑥3 + 𝑎𝑥 + 𝑏
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY 3
𝐸(−1,0)
𝐸(1,1)

4. Geometric description of addition
• A group can be defined based on the set 𝐸(𝑎, 𝑏) for specific values of 𝑎 and 𝑏 in the elliptic curve equation, provided it
satisfied the following condition:
4𝑎3 + 27𝑏2 ≠ 0
• Let + be defined as addition for the set 𝐸(𝑎, 𝑏) where 𝑎 and 𝑏 satisfy the above equation
• In geometric terms, the rules for addition can be stated as follows:
If three points on an elliptic curve lie on a straight line, their sum is 𝑶
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY 4

5. Rules of addition over elliptic curve
1. 𝑂 serves as the additive identity. Thus 𝑂 = −𝑂; for any point 𝑃 on the elliptic curve, 𝑃 + 𝑂 = 𝑃. In what follows, we assume 𝑃 ≠
𝑂 and 𝑄 ≠ 𝑂.
2. The negative of a point 𝑃 is the point with the same 𝑥 coordinate but the negative of the 𝑦 coordinate; that is, if 𝑃 = (𝑥, 𝑦), then
− 𝑃 = (𝑥, −𝑦). Note that these two points can be joined by a vertical line. Note that 𝑃 + (−𝑃) = 𝑃 − 𝑃 = 𝑂.
3. To add two points 𝑃 and 𝑄 with different 𝑥 coordinates, draw a straight line between them and find the third point of intersection 𝑅. It
is easily seen that there is a unique point 𝑅 that is the point of intersection (unless the line is tangent to the curve at either 𝑃 or 𝑄, in
which case we take 𝑅 = 𝑃 or 𝑅 = 𝑄, respectively). To form a group structure, we need to define addition on these three points: 𝑃 +
𝑄 = −𝑅. That is, we define 𝑃 + 𝑄 to be the mirror image (with respect to the 𝑥 axis) of the third point of intersection.
4. The geometric interpretation of the preceding item also applies to two points, 𝑃 and −𝑃, with the same 𝑥 coordinate. The points are
joined by a vertical line, which can be viewed as also intersecting the curve at the infinity point. We therefore have 𝑃 + (−𝑃) = 𝑂,
which is consistent with item (2).
5. To double a point 𝑄, draw the tangent line and find the other point of intersection 𝑆. Then 𝑄 + 𝑄 = 2𝑄 = −𝑆.
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY 5

6. Cryptographic Implementation
Two families of elliptic curves are used in cryptographic applications:
• Prime curves over 𝑍 𝑝
• Binary curves over 𝐺𝐹(2 𝑚)
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY 6

7. Prime curves over 𝑍 𝑝
• Cubic equation in which the variables and coefficients take on values in set of integers from 0 through 𝑝 − 1
• Calculations are performed modulo 𝑝
• Best for software applications
𝑦2 𝑚𝑜𝑑 𝑝 = (𝑥3 + 𝑎𝑥 + 𝑏) 𝑚𝑜𝑑 𝑝
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY 7

8. Binary curves over 𝐺𝐹(2 𝑚)
• The variables and coefficients take on values in 𝐺𝐹(2 𝑚)
• Calculations are performed over GF(2m)
• Best for hardware applications
𝑦2 + 𝑥𝑦 = 𝑥3 + 𝑎𝑥2 + 𝑏
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY 8

9. ECC Diffie-Hellman Key Exchange
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY 9
Global Public Elements
𝐸 𝑞(𝑎, 𝑏) elliptic curve with parameters 𝑎, 𝑏, and 𝑞, where 𝑞
is a prime or an integer of the form 2 𝑚
𝐺 point on elliptic curve whose order is large value 𝑛
User A key generation
Select private 𝑛 𝐴 𝑛 𝐴 < 𝑛
Calculate public 𝑃 𝐴 𝑃 𝐴 = 𝑛 𝐴 × 𝐺
User B key generation
Select private 𝑛 𝐵 𝑛 𝐵 < 𝑛
Calculate public 𝑃 𝐵 𝑃 𝐵 = 𝑛 𝐵 × 𝐺
Calculation of secret key by User A
𝐾 = 𝑛 𝐴 × 𝑃𝐵
Calculation of secret key by User B
𝐾 = 𝑛 𝐵 × 𝑃𝐴

10. References
Schneier, B. (2007). Applied cryptography: protocols, algorithms, and source code in C. John Wiley & Sons.
Stallings, W. (2014). Cryptography and network security, 6/E. Pearson Education India.
Katz, J., & Lindell, Y. (2014). Introduction to modern cryptography. CRC press.
Washington, L. C. (2008). Elliptic curves: number theory and cryptography. CRC press
UITC203 CRYPTOGRAPHY AND NETWORK SECURITY 10