Elliptic curve cryptography (ECC) uses elliptic curves over finite fields to provide public-key encryption and digital signatures. ECC requires significantly smaller key sizes than other cryptosystems like RSA to provide equivalent security. This allows for faster computations and less storage requirements, making ECC ideal for constrained environments like smartphones. ECC relies on the difficulty of solving the elliptic curve discrete logarithm problem to provide security.

1. Elliptic Curve
Cryptography

2. Introduction
• ECC was introduced by Victor Miller and Neal Koblitz in 1985.
• For DSA, RSA we need larger key length.
• ECC requires significantly smaller key size with same level of
security.
• Benefits of having smaller key sizes : faster computations, need
less storage space.
• ECC ideal for constrained environments : Pagers ; PDAs ;
Cellular Phones ; Smart Cards
2

3. Group
A group is an algebric system consisting of a set G together with a binary
operation * defined on G satisfying the following axioms :
1. Closure : for all x,y in G we have x * y ∈ G
2. Associativity : for all x,y and z in G we have (x
* y) * z = x * (y * z)
3. Identity : there exists an e in G such that x * e = e * x = x for all
x
4. Inverse : for all x in G there exists y in G such that x *
y = y * x = e
In addition if for x, y in G we have x * y = y * x then we say that group G is
abelian.
3

4. Finite Field
A finite field is an algebric system consisting of a set F together with a
binary operations + and * defined on F satisfying the following axioms :
1. F is an abelian group with respect to +.
2. F {0} is an abelian group with respect to *.
3. For all x, y and z in F we have
x * ( y + z) = (x * y) + (x * z)
(x + y) * z = (x * z) + (y * z)
The order of the finite field is the number of elements in the field.
4

5. Galois Fields
The polynomials
Zp[x] mod p(x)
where
p(x) ∈ Zp[x],
p(x) is irreducible,
and deg(p(x)) = n (i.e., n+1 coefficients)
form a finite field. Such a field has pn
elements.
These fields are called Galois Fields or GF(pn
).
The special case n = 1 reduces to the fields Zp
The multiplicative group of GF(pn
)/{0} is cyclic .

6. Galois Field GF(p)
It is a finite field and it consists of a set of integers {0,1,2,3….p-1} where p
is a prime number. Additionally it satisfies the following arithmetic
operations :
1. Addition : if a, b ∈ GF(p), then a + b = r where r is the
remainder of the division of a + b by p and 0<= r <= p-1. This
operation is called addition modulo p.
2. Multiplication : if a, b ∈ GF(p), then a . b = s where s is the
remainder of the division of a . b by p and 0<= s <= p-1. This
operation is called multiplication modulo p.
6

7. Galois Field GF(2m
)
It is a finite field and is called binary finite field. It is a vector space
of dimension m over GF(2) i.e. there exists a set of m elements {αm-
1, …,α1, α0} each αi ∈ {0,1} in GF(2m
) such that each a ∈ GF(2m
)
a = αm-1xm-1
+ … + α1x + α0
Additionally it satisfies the following arithmetic operations :
a = {am-1,..a1,a0} and b = {bm-1,..b1,b0} ∈ GF(2m
)
• Addition : a + b = c = {cm-1,..c1,c0} where ci = (ai + bi) mod 2. c
∈ GF(2m
)
• Multiplication : a . b = c = {cm-1,..c1,c0} where c is the
remiander of the division of the polynomial a(x) . b(x) by an
irreducible polynomial of degree m. c ∈ GF(2m
)
7

8. Definition of Elliptic curves
An elliptic curve over a field K is a nonsingular
cubic curve in two variables, f(x,y) =0 with a
rational point (which may be a point at infinity).
The field K is usually taken to be the complex
numbers, reals, rationals, algebraic extensions of
rationals, p-adic numbers, or a finite field.
Elliptic curves groups for cryptography are
examined with the underlying fields of Fp (where
p>3 is a prime) and F2
m
(a binary representation
with 2m
elements).

9. General form of a EC
An elliptic curve is a plane curve defined by an
equation of the form
baxxy ++= 32
Examples

10. Let GF(p) be a finite field, p > 3, and let a, b ∈ GF(p) are
constant such that
4a3
+ 27b2
≡ 0 (mod p).
An elliptic curve, E(a,b)
(GF(p)), is defined as the set of points
(x,y) ∈ GF(p) * GF(p) which satisfy the equation
y2
≡ x3
+ ax + b (mod p)
together with a special point, O, called the point at infinity.
Elliptic Curve over GF(p)
10

11. P and Q be two points on E(a,b)
(GF(p)) and O is the point at infinity.
• P+O = O+P = P
• If P = (x1
,y1
) then -P = (x1
,-y1
)
and P + (-P) = O.
• If P = (x1
,y1
) and Q = (x2
,y2
), and P and Q are not O.
then P +Q = (x3
,y3
) where
x3
= λ2
- x1
- x2
y3
= λ(x1
- x2
) - y1
and λ = (y2
-y1
)/(x2
-x1
) if P ≠ Q
Elliptic Curve over GF(p)
11

12. Task 1 - Multiplication c = a.b in GF11
 Compile a multiplication table for c = a . b mod 11
 Determine the solutions of the equation x2
= 5 mod 11
 You have about 10 minutes for this task

13. Solution 1 : Multiplication c = a.b in
GF11
 x2
= 5 mod 11 ?
 x1 = 4, x2 = 7

14. Task 2 : Iterate a Point on the
Elliptic Curve
 Iterate the point P(2,4) lying on y2
= x3
+ x + 6 mod 11:
 Compute P2 = P  P by doubling the point P
 Compute P3 = P  P  P = P2  P by point addition
 All operations are computed in GF11

15. • Elliptic curve E(a,b)
(GF(2m
)) is defined to be
the set of points (x,y) ∈ GF(2m
) * GF(2m
) which satisfy the
equation
y2
+ xy = x3
+ ax2
+ b;
where a, b ∈ GF(2m
) and b≠0,
together with the point on the curve at infinity, O.
• The points on an elliptic curve form an abelian group under a
well defined group operation.
The identity of the group operation is the point O.
Elliptic Curve over GF(2m
) for some m ≥ 1.
15

16. Elliptic Curve over GF(2m
) for some m ≥ 1.
P and Q be two points on E(a,b)
(GF(2m
)) and O is the point at infinity.
• P+O = O+P = P
• If P = (x1
,y1
) then -P = (x1
,-y1
)
and P + (-P) = O.
• If P = (x1
,y1
) and Q = (x2
,y2
), and P and Q are not O, then P +Q =
(x3
,y3
):
if P ≠ Q
x3
= λ2
+ λ + x1
+ x2
+ a
y3
= λ(x1
+ x3
) + x3
+ y1
and
λ = (y1
+y2
)/(x1
+x2
)
if P = Q
x3
= λ2
+ λ + a
y3
= x1
2
+ (λ + 1)x 1
16

17. What Is Elliptic Curve
Cryptography (ECC)?
Elliptic curve cryptography [ECC] is a public-key
cryptosystem just like RSA, Rabin, and El Gamal.
Every user has a public and a private key.
 Public key is used for encryption/signature verification.
 Private key is used for decryption/signature generation.
Elliptic curves are used as an extension to other
current cryptosystems.
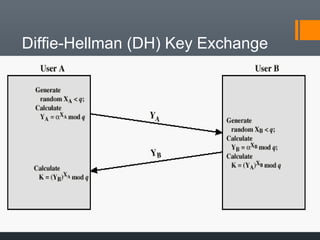
 Elliptic Curve Diffie-Hellman Key Exchange
 Elliptic Curve Digital Signature Algorithm

18. Using Elliptic Curves In Cryptography
The central part of any cryptosystem involving
elliptic curves is the elliptic group.
All public-key cryptosystems have some
underlying mathematical operation.
RSA has exponentiation (raising the message or
ciphertext to the public or private values)
ECC has point multiplication (repeated addition of two
points).

19. Elliptic Curve Discrete Logarithm
Problem (ECDLP)
 Given an elliptic curve
y2 = x3 + ax + b mod p and
a basis point P,
we can compute Q = Pk through k-1
iterative point additions.
 Fast algorithms for this task exist.
 Question: Is it possible to compute k
when the point Q is known?
 Answer: This is a hard problem known as
the Elliptic Curve Discrete Logarithm.

20. ECC Domain Parameters
ECC domain parameters over GF(q), are a six tuple:
T = (q, a, b, G, n, h)
• q = p or q = 2m
• a and b ∈ GF(q)
y2
≡ x3
+ ax + b (mod p) for q = p > 3
y2
+ xy = x3
+ ax2
+ b for q = 2m
≥ 1
• a base point G = (xG
,yG
) on E(a,b)(
GF(q)),
• a number n which is the order of G
(The order of a point P on an elliptic curve is the smallest
positive integer n such that nP = O.)
• h = #E/n. where #E represents number of points on elliptic
curve and is called the curve order.
20

21. Key Generation
 Agree on the following (public):
 Curve parameters (a, b)
 The modulus p
 Base point G (on the curve)
 Pick a random integer n as private key
 Calculate public key P = n*G
21

22. Diffie-Hellman (DH) Key Exchange

23. ECC Diffie-Hellman
Public: Elliptic curve and point G=(x,y) on curve
Secret: Alice’s a and Bob’s b
Alice, A Bob, B
a(x,y)
b(x,y)
• Alice computes a(b(x,y))
• Bob computes b(a(x,y))
• These are the same since ab = ba

24. Example – Elliptic Curve
Diffie-Hellman Exchange
 Alice and Bob want to agree on a shared key.
 Alice and Bob compute their public and private keys.
 Alice
 Private Key = nA
 Public Key = PA = nA* G
 Bob
 Private Key = nB
 Public Key = PB = nB * G
 Alice and Bob send each other their public keys.
 Both take the product of their private key and the other user’s
public key.
 Alice  KAB = PB*nA = (nB * G)*nA
 Bob  KAB = PA* nB = (nA* G)*nB
 Shared Secret Key = KAB = nA *nB * G

25. Encryption/Decryption
 Alice represents her text or data to send as a point Pm
 Alice sends Bob a pair of points:
Cm= {k*G, Pm + k*PB}
where k = randomly chosen integer
 Bob decrypts the message using his private key:
Pm + k*P – nB (k*G) = Pm + k(nB *G) - nB (k*G) = Pm
25

26. Example – Elliptic Curve Cryptosystem
Analog to El Gamal
Suppose Alice wants to send to Bob an encrypted
message.
 Both agree on a base point, G.
 Alice and Bob create public/private keys.
 Alice
 Private Key = a
 Public Key = PA = a* G
 Bob
 Private Key = b
 Public Key = PB = b * G
 Alice takes plaintext message, M, and encodes it onto a
point, PM, from the elliptic group

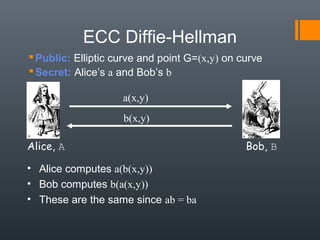
27. Example – Elliptic Curve Cryptosystem
Analog to El Gamal
Alice chooses another random integer, k from
the interval [1, p-1]
The ciphertext is a pair of points
 CM = [ (kG), (PM + kPB) ]
To decrypt, Bob computes the product of the first
point from PC and his private key, b
 b * (kG)
Bob then takes this product and subtracts it from
the second point from PC
 (PM + kPB) – [b(kG)] = PM + k(bG) – b(kG) = PM
Bob then decodes PM to get the message, M.

28. Example – Compare to El Gamal
The ciphertext is a pair of points
 CM = [ (kG), (PM + kPB) ]
The ciphertext in El Gamal is also a pair.
 C = (gk
mod p, mPB
k
mod p)
------------------------------------------------------------------
-Bob then takes this product and subtracts it
from the second point from PC
 (PM + kPB) – [b(kG)] = PM + k(bG) – b(kG) = PM
In El Gamal, Bob takes the quotient of the
second value and the first value raised to Bob’s
private value
 m = mPB
k
/ (gk
)b
= mgk*b
/ gk*b
= m

29. Why use ECC?
How do we analyze Cryptosystems?
 How difficult is the underlying problem that it is based upon
 RSA – Integer Factorization
 DH – Discrete Logarithms
 ECC - Elliptic Curve Discrete Logarithm problem
 How do we measure difficulty?
 We examine the algorithms used to solve these problems

30. Security of ECC
 The difficult mathematical problem is called the
 elliptic curve discrete logarithm problem
 That is, given P and G, (and P= n*G), find n
 not susceptible to common attacks
 Runs in exponential time
 RSA runs in sub-exponential time

31. Applications of ECC
Many devices are small and have limited
storage and computational power
Where can we apply ECC?
 Wireless communication devices
 Smart cards
 Web servers that need to handle many encryption
sessions
 Any application where security is needed but
lacks the power, storage and computational
power that is necessary for our current
cryptosystems

32. Benefits of ECC
Same benefits of the other cryptosystems:
confidentiality, integrity, authentication and non-
repudiation but…
Shorter key lengths
 Encryption, Decryption and Signature Verification speed
up
 Storage and bandwidth savings

33. Summary of ECC
“Hard problem” analogous to discrete log
 Q=kP, where Q,P belong to a prime curve
given k,P  “easy” to compute Q
given Q,P  “hard” to find k
 known as the elliptic curve logarithm problem
 k must be large enough
ECC security relies on elliptic curve logarithm
problem
 compared to factoring, can use much smaller key sizes
than with RSA etc
 for similar security ECC offers significant
computational advantages