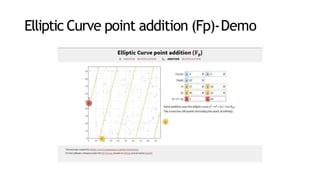
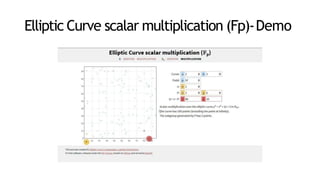
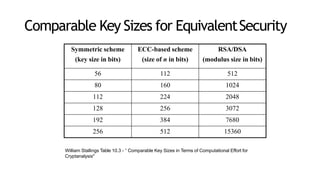
This document provides an introduction to elliptic curve cryptography (ECC). It explains that ECC uses smaller key sizes than RSA for an equivalent security level. ECC performs computations using elliptic curve arithmetic over finite fields rather than integer arithmetic. The document covers elliptic curves over real numbers and finite fields, point addition and scalar multiplication, the discrete logarithm problem that ECC is based on, applications of ECC, and its security advantages compared to RSA. Interactive demos are included to demonstrate point addition and scalar multiplication on elliptic curves over both real numbers and finite fields.

1. Elliptic Curve Cryptography

2. Agenda
• Introduction
• Elliptic Curves Over the Real Numbers
• Elliptic Curves Over a Finite Field
• Elliptic Curve Cryptography Demo
• Elliptic Curve Cryptography – Key
Exchange

3. Introduction
• Major issue with use of public key is the size of numbers used.
• ECC belongs to the category of Public-key Cryptography,
performs the computations using elliptic curve arithmetic
instead of integer or polynomial arithmetic.
• ECC provides equally good security compared to RSA, but uses
smaller key size.
• Notable Advantages of ECC
• Uses smaller keys, ciphertexts and signatures.
• ECC supports, very fast key generation.
• ECC scores over RSA because of its moderately fast encryption and
decryption.
• ECC computations are uses less memory and CPU cycles compared to
RSA, hence
suited for securing Mobile Handheld devices.

4. Comparable Key Sizes for EquivalentSecurity
Symmetric scheme
(key size in bits)
ECC-based scheme
(size of n in bits)
RSA/DSA
(modulus size in bits)
56 112 512
80 160 1024
112 224 2048
128 256 3072
192 384 7680
256 512 15360
William Stallings Table 10.3 - “ Comparable Key Sizes in Terms of Computational Effort for
Cryptanalysis"

5. Introduction
• An elliptic curve is defined by an equation in two variables
with coefficients.
• Elliptic curves are not ellipses. Elliptic curves are described by
cubic equations similar to those used for calculating the
circumference of an ellipse
• Elliptic curve cryptography makes use of elliptic curves, in
which the variables and coefficients are all restricted to
elements of a finite field.

6. ECC over RealNumbers
• Elliptic curve over real numbers are nothing but set of points (x,y)
which
satisfy an elliptic curve equation y2 = x3 + ax + b, where x, y, a
and b are real numbers.
• Supplying different set of values for a and b results in a different
elliptic curve.
• For example a = -4 and b = 0.67 gives the elliptic curve with
equation y2 = x3 - 4x + 0.67
• If the cubic polynomial x3+ax+b has no repeated roots, we say the
elliptic curve is non-singular.
• A necessary and sufficient condition for the cubic polynomial
x3+ax+b to have distinct roots is 4a^3 + 27 b^2 not equal to 0.
• we’ll always assume the elliptic curves are non-singular.

7. P + Q = R is the additive property defined
geometrically

8. Elliptic Curves Over FiniteFields
• Instead of choosing the field of real numbers, we can create elliptic
curves over other fields!
• Let a and b be elements of Zp for p prime, p>3. An elliptic curve E
over Zp is the set of points (x,y) with x and y in Zp that satisfy the
equation
together with a single element , called the point at infinity.
• As in the real case, to get a non-singular elliptic curve, we’ll require 4a3
+ 27 b2 (mod p)  0 (mod p).
• Elliptic curves over Zp will consist of a finite set of points

9. Elliptic Curves Over FiniteFields
• Just as in the real case, we can define addition of points on an
elliptic curve E over Zp, for prime p>3.
• This is done in the essentially the same way as the real
case, with appropriate modifications.

10. Point Addition over FiniteFieldFp
• Point addition and doubling
are now slightly different
visually.
• Lines drawn on this graph
will wrap around the
horizontal and vertical
directions, just like in a
game of Asteroids,
maintaining the same slope.
• So adding points (2, 22) and
(6,
25) looks like this:
• The third intersecting point is
(47, 39) and its reflection point
is (47, 28).
Ref: http://www.coindesk.com/math-behind-
bitcoin/

11. Elliptic Curve CryptographyDiscrete
Logarithm Problem [ ECCDLP]
• Addition is simple
P + P = 2P
Multiplication is faster , it takes only 8 steps to compute 100P, using point doubling
and add 1. P * 2 = 2P
2. P + 2P = 3P
3. 3P * 2 = 6P
4. 6P *2 = 12P
5. 12P * 2 =24 P
6. P + 24 P = 25 P
7. 25P * 2 = 50 P
8. 50P *2 = 100 P

12. Elliptic Curve CryptographyDiscrete
Logarithm Problem [ ECCDLP]
• Division is slow,
• In ECC Q is defined as product of n*P is another point on
the curve
Q = nP
given initial point P and final point Q, it is hard to
compute ‘n’ which serves as a secret key.
Brute force method, start with P,every step multiply P
with number 1, 2 and so on,
For each step compare result of P*x where x=1,2,3,…
with Q This problem is known as discrete log problem,
difficult to beak

13. Elliptic Curve point addition (R)-Demo

14. Elliptic Curve scalar multiplication (R)-Demo

15. Elliptic Curve point addition (Fp)-Demo

16. Elliptic Curve scalar multiplication (Fp)-Demo

17. ECCApplication
• ECC is being used in many places
such as
• PDAs
• VOIP
• Smart cards
• Mobile devices

18. Diffie-Hellman Key Exchange – ECC scenario
• Alice and Bob two parties need to exchange secret key
1. Both Alice and Bob agree upon starting point P point on
elliptic curve publicly defined y2 = x3 - 4x + 0.67
2. Alice selects his private ‘α’ and computes αP shares this
with bob
3. Bob selects his private ‘β’ and computes βP shares with Alice
4. Alice receives βP and computes βPα by multiplying with his
private
5. Bob receives αP and computes αPβ by multiplying with his
private

19. Security Aspect
• Attacks on groups of elliptic curves are weaker than available
factoring algorithms attacks
• Best known attacks on elliptic curves based on cryptographic
criterions are the Baby-Step Giant-Step and Pollard-Rho method
• Complexity of these methods are approximately √ p .
• An elliptic curve using a prime p with 160 bit ,roughly 2160 points,
provides a security of 280 steps on an average that is
required by an attacker.
• An elliptic curve using a prime p with 256 bit, roughly 2256 points,
provides a
security of 2128 steps on an average.

20. Reference
1. Network security and cryptography - William Stallings
2. Kwangjo Kim, Cryptography, Open Access Journal
3. Elliptic Curve Cryptography - Lecture notes by Wayne
Patterson
4. Elliptic Curve Cryptography: a gentle introduction,
http://andrea.corbellini.name/2015/05/17/elliptic-
curve- cryptography-a-gentle-introduction/
5. Certicom, https://www.certicom.com/ecc

22. Presented by: Ayush Jain
IU1941090004
EC 7TH Sem.