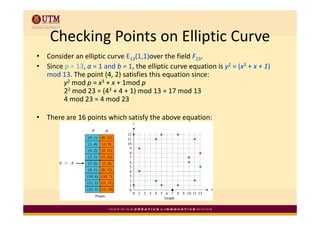
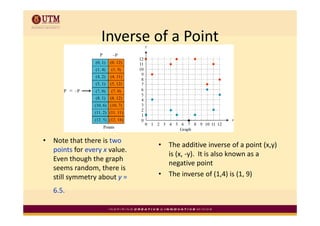
Elliptic curve cryptography uses elliptic curves over finite fields for public-key encryption. It offers the same security as other public-key cryptosystems using smaller key sizes. The points on an elliptic curve over a finite field form a finite abelian group which can be used for cryptographic operations like point addition. Point addition involves calculating the slope between two points and using it to find the x-coordinate of the sum point, while point doubling uses the tangent line to find the double of a point.

1. Elliptic Curve Cryptography
Introduction
Addition of Points in Elliptic Curve
Additi f P i t i Elli ti C
Key Exchange
y g
Encryption

2. Elliptic Curve Cryptography
Elliptic Curve Cryptography
• Majority of public‐key crypto (RSA, D‐H) use
g p y
either integer or polynomial arithmetic with
very large numbers/polynomials.
• This imposes a significant load in storing and
This imposes a significant load in storing and
processing keys and messages.
• An alternative is to use elliptic curves (ECC).
• ECC offers the same security with smaller bit
ECC offers the same security with smaller bit
sizes

3. Key Size
Key Size
• Symmetric vs public‐key vs ECC key sizes
Symmetric Public‐key ECC
(40 bits) — —
56 bits (400 bits) —
64 bits 512 bits —
80 bits
80 bits 768 bits
768 bits —
90 bits 1024 bits 160 bits
112 bits 1792 bits 195 bits
120 bits 2048 bits 210 bits
128 bits 2304 bits 256 bits

4. Elliptic Curves over Real Numbers
Elliptic Curves over Real Numbers
• An elliptic curve is defined by an equation in two variables x & y, with
An elliptic curve is defined by an equation in two variables x & y with
coefficients
• The general equation for an elliptic curve is
• Elliptic curves over real numbers use a special class of elliptic curves
Elli ti l b i l l f lli ti
of the form
– y2 = x3 + ax + b (equation 1)
– where x, y, a, b are all real numbers
– also define zero point O (also known as infinity point)
– If the curve has no repeated factors, then the following condition is true:
4a3 +27b2 <> 0
• The set of points E(a,b) which consists of all points (x,y) satisfy the
( q
(equation 1) together with the element O.
) g

5. Examples of Real Elliptic Curves
Examples of Real Elliptic Curves
• Figures below shows two elliptic curves with equations y2 = x3 − 4x and y2
b l h ll h d
= x3 − 1. Both are nonsingular. However, the first has three real roots (x =
−2, x = 0, and x = 2), but the second has only one real root (x = 1) and two
imaginary ones.

6. Checking a Point on the Curve
Checking a Point on the Curve
• Is (4,7) a point on the elliptic curve y2= x3‐ 5x +
5 over real numbers?
• Yes since the equation holds true for x = 4 and
Yes, since the equation holds true for x = 4 and
y = 7:
( )2= (4)3‐ 5(4) + 5
(7) ( ) ( )
49 = 64 ‐ 20 + 5
49 = 49

7. Elliptic Curve Groups over F
Elliptic Curve Groups over Fp
• E
Essential property for cryptography is that a group has a finite
i l f h i h h fi i
number of points.
• Calculations over the real numbers are slow and inaccurate
Calculations over the real numbers are slow and inaccurate
due to round‐off error.
• Cryptographic applications require fast and precise arithmetic;
thus elliptic curve groups over the finite fields of Fp and F2m
are used in practice.
• Field Fp uses the numbers from 0 to p ‐ 1 and computations
Field F uses the numbers from 0 to p 1, and computations
end by taking the modulo of p.
– For example, in F23 the field is composed of integers from 0 to
p , p g
22, and any operation within this field will result in an integer
also between 0 and 22.

8. Finite Elliptic Curves
Finite Elliptic Curves
• Elliptic curve cryptography uses curves whose
variables & coefficients are finite
• have two families commonly used:
– prime curves Ep( b) d fi d
i E (a,b) defined over Zp
Z
• use integers modulo a prime
• best in software
– binary curves E2m(a,b) defined over GF(2m)
• use polynomials with binary coefficients
• best in hardware

9. Fp
• An elliptic curve with the underlying field of Fp can be formed by choosing
A lli ti ith th d l i fi ld f F b f db h i
the variables a and b within the field of Fp. The elliptic curve includes all
points (x, y) which satisfy the elliptic curve equation modulo p (where x
and y are numbers in F ).
and y are numbers in Fp)
• For example: y2 mod p = x3 + ax + b mod p has an underlying field of Fp if a
and b are in Fp. The curve can be noted as Ep(a,b).
• If x3 + ax + b contains no repeating factors (or, equivalently, if 4a3 + 27b2
mod p <> 0), then the elliptic curve can be used to form a group.
• An elliptic curve group over Fp consists of the points on the corresponding
elliptic curve, together with a special point O called the point at infinity.
There are finitely many points on such an elliptic curve.

10. Checking Points on Elliptic Curve
Checking Points on Elliptic Curve
• Consider an elliptic curve E13(1,1)over the field F23.
• Since p = 13, a = 1 and b = 1, the elliptic curve equation is y2 = (x3 + x + 1)
mod 13. The point (4, 2) satisfies this equation since:
y2 mod p = x3 + x + 1mod p
22 mod 23 = (43 + 4 + 1) mod 13 = 17 mod 13
4 mod 23 = 4 mod 23
• There are 16 points which satisfy the above equation:

11. Inverse of a Point
Inverse of a Point
• Note that there is two
N t th t th i t
• The additive inverse of a point (x,y)
points for every x value.
is (x, ‐y). It is also known as a
Even though the graph
negative point
negative point
seems random, there is
still symmetry about y = • The inverse of (1,4) is (1, 9)
6.5.
65

12. Exercise
• Does the elliptic curve equation y2 = x3 +10x
+5 define a group over F17?
g p
• a = 10, b = 5, p = 17
4a3 +27b2 mod 17 = 4(10)3 +27(5)2 mod 17
= 4675 mod 17
= 0
• Therefore the curve does not define a group.

13. Activity 1
Activity 1
• Does the elliptic curve equation
Does the elliptic curve equation
y2 = x3 +x +6
define a group over F11?
• Write the equation in terms of Ep(a,b).

14. Addition of Points in EC

15. Addition Rules over an Elliptic Curve
Addition Rules over an Elliptic Curve
• P+Q+R = O if P, Q and R are three points on an elliptic curve that lie on a
P Q R O if P Q d R th i t lli ti th t li
straight line.
• O = ‐O; P+O =P: then O is an additive identity
• The negative of a point P is the point with the same x coordinate but the
The negative of a point P is the point with the same x coordinate but the
negative of the y coordinate (i.e. if P1 = (x,y) and P2 = (x, ‐y), then P1 = ‐P2.
• To add 2 point P and Q with different coordinates:
T dd 2 i t P d Q ith diff t di t
– Q+R+P1 = O, Therefore Q+R = ‐P1
• To double a point Q, draw the tangent line and find the other point of
intersection S. Then Q+Q = 2Q = ‐S (Note: Q+R+S = O, If R=Q, then 2Q =‐S).

16. Adding 2 points: P+Q
Adding 2 points: P+Q
• R ll th t i
Recall that a is one of the parameters chosen with the elliptic
f th t h ith th lli ti
curve and that λ is the tangent on the point P.
• The negative of the point P = (xP, yP)
is the point ‐P = (xP, ‐yP mod p).
• If P = (x1, y1) and Q = (x2, y2) are distinct points such that P is
not ‐Q, then P + Q = R where (meaning have different
coordinates)
λ = (y2 – y1) / (x2 – x1) mod p
x3 = λ 2 – x1 – x2 mod p
y3 = y1 + λ(x1 – x3) mod p
= ‐y + ) mod p
• Note that λ is the slope of the line through P and Q.

17. Doubling the point P
Doubling the point P
• Provided that y1 is not 0, 2P = R where
λ = (3x12 + a) / (2y1 ) mod p
x3 = λ 2 ‐ 2x1 mod p
= mod p
y3 = ‐y1 + λ(x1 – x3) mod p

18. Example: The Negative Points
Example: The Negative Points
• What are the negatives of the following
elliptic curve points over F17?
p p
P=(5,8) Q=(3,0) R=(0,6)
• The negative of a point P = (xP, yP) is the point
‐P = (xP, ‐yP mod p).
( )
• Thus ‐P=(5,9) ‐Q=(3,0) ‐R=(0,11)

19. Example: Adding 2 Points
Example: Adding 2 Points
In the elliptic curve group defined by y2 = x3 + x + 7 over F17,
• I h lli i d fi d b 3 7 F
what is P + Q if P = (2,0) and Q = (1,3)?
• λ = (y2 – y1) / (x2 – x1) mod p
= (y ) / (x ) mod p
= (‐3) / 1 mod 17
= ‐3 mod 17 = 14
x3 = λ 2 – x1 – x2 mod p
d
= 196 ‐ 2 ‐ 1 mod 17
= 193 mod 17 = 6
y3 = ‐y1 + λ(x1 – x3) mod p
= 0 + 14*(2 ‐ 6) mod 17
= ‐56 mod 17 = 12
= 56 mod 17 = 12
• Thus P + Q = (6,12)
Q ( , )

20. Example: Doubling the Points
Example: Doubling the Points
In the elliptic curve group defined by y2 = x3 + x + 7 over F17,
• I h lli i d fi d b 7 F
what is 2P if P = (1, 3)?
• λ = (3x12 + a) / (2y1 ) mod p
= (3 + 1) * 6‐1 mod 17
= 4 * 3 mod 17 = 12
4*3 d 17 12
x3 = λ 2 ‐ 2x1 mod p
= 144 ‐ 2 mod 17
= 142 mod 17 = 6
y3 = ‐y1 + λ(x1 – x3) mod p
= ‐3 + 12 * (1 ‐ 6) mod 17 = ‐63 mod 17 = 5
= 3 + 12 * (1 6) mod 17 = 63 mod 17 = 5
• Thus 2P = (6 5)
Thus 2P = (6,5)

21. Elliptic Curve: y2
Elliptic Curve: y2 = x3+x+6(mod11)
• All the points on the curve are:
(2, 4)
(2, 4) (7, 2)
(7, 2)
(2, 7) (7, 9)
(3, 5) (8, 3)
(3, 6)
(3 6) (8, 8)
(8 8)
(5, 2) (10, 2)
(5, 9) (10, 9)

22. Activity 2
Activity 2
• Given P = (2, 4) and Q = (3, 5)
• Calculate :
Calculate :
– P+Q
– 2P
– 3P
– 4P
–DDoes 4P = 3P + P = 2P + 2P?
4P 3P P 2P 2P?

23. Generating Public and Private Keys
Generating Public and Private Keys
• can do key exchange analogous to D‐H
• users select a suitable curve Ep(a,b)
users select a suitable curve E
• select base point G=(x1,y1) with large order n
such that nG=O
h h
• A & B select private keys nA<n, nB<n
p y ,
• compute public keys: PA=nA×G, PB=nB×G

24. Determining n
Determining n
Starting with P = (2, 7), 2P = P + P
λ = (3 * 22 + 1) / (2 * 7)
3-1 mod 11
= (13 mod 11)/ (14 mod 11) = 39 mod 11
32 mod 11=9
= (2 mod 11) / (3 mod 11) 34 mod 11=81 mod 11=4
= 2 *4 = 8 38 mod 11=16 mod 11=5
39 mod 11= (38 × 3) mod 11
x3 = 82 ‐ 2 ‐ 2 (mod 11) = (5 × 3) mod 11
= 5 = 15 mod 11
=4
y3 = 8 (2 ‐ 5) ‐ 7 (mod 11)
= 2
Therefore, P + P = (2, 7) + (2, 7) = (5, 2).

25. Multiples of P
Multiples of P
2P = (5, 2) 3P = (8, 3)
4P = (10, 2)
(10, 2) 5P = (3, 6)
(3, 6)
6P = (7, 9) 7P = (7, 2)
8P = (3, 5) 9P = (10, 9)
10P = (8 8)
= (8, 8) 11P = (5 9)
= (5, 9)
12P = (2, 4) 13P = O

26. RECALLING KEY GENERATION
RECALLING KEY GENERATION
Global Public Elements:
Gl b l P bli El t
Ep(a,b) – elliptic curve G – point on elliptic curve
Alice Bob
• Key Generation • Key Generation
– Alice selects a private no.
p – Bob selects a private no.
p
• nA < n • nB < n
– Alice calculates her public – Bob calculates his public
key
k key
k
• PA = nA × G • PB = nB × G

27. Key Generation
Key Generation
• Recall equation y2 = x3+x+6(mod11)
• Select G(x1, y1) = (2, 7)
and Ep(a,b) = E11(1, 6) where they are known to both parties.
• Alice chooses a Private key :
Alice chooses a Private key
– Select integer nA = 7 < n, where nG = O.
– In this case n = 13
• Alice’s Public key :
– PA = nA * G ∈ E11(1,6)
= 7 (2 7)
= 7 * (2, 7)
= (7, 2)

28. Activity 3
Activity 3
• You are Bob:
• Choose a private key
Choose a private key
• Calculate your public key
– PB = nB × G

29. ECC Encryption/Decryption
ECC Encryption/Decryption
• several alternatives, will consider simplest
• must first encode any message M as a point on the elliptic
curve Pm
P
• select suitable curve & point G as in D‐H
• each user chooses private key nA<n
h h i t k Message M
• and computes public key PA=nA×G Bob’s public key
• to encrypt Pm : Cm={kG, Pm+k PB}, k random
k d
• decrypt Cm compute:
Pm+kPB–nB(kG) = Pm+k(nBG)–nB(kG) = Pm
Bob’s private key

30. Example: Encryption
Example: Encryption
• Encrypt pm = (10, 9), k = 3, G(2, 7)
Private key, KBpr = 7 ( < 13)
y Bpr ( )
Public key KBpu = (7, 2)
• cm = {kG pm + kKBpu }
= {kG, p + kK
= {3(2, 7), (10, 9) + 3(7, 2)}
= {(8, 3), (10, 9) + (3, 5)}
{( ) ( ) ( )}
= {(8, 3), (10, 2)}

31. Example: Decryption
Example: Decryption
• Procedure:
– Receiver multiplies the first point in the pair by
p p p y
the receiver’s secret key
KBpr(kG) = 7*(8, 3) = (3, 5)
( ) ( , ) ( , )
– Subtracts the result from the second point.
(pm + kKBpu) KBpr(kG)
+ kK ) ‐
= Pm +k(KBprG) – KBpr(kG) = Pm
(10, 2) – (3, 5) = (10,2) + (– (3, 5)) = ?
What is the +ve value of this?
ve
y2 = x3+x+6(mod11)

32. Security Strength
Security Strength
• The security of ECC depends on how to determine k given kP and P.
h f d d h d k k d
This is referred to as elliptic curve logarithm problem.
• The fastest method for taking the elliptic curve logarithm is “Pollard
g p g
rho method”.
• Compared to factoring, can use much smaller key sizes than with RSA
etc
etc
• Eg. To solve logarithm problem for ECC with key size = 150 bit takes
more time than factoring problem of 512 bit key size of RSA.
• For equivalent key lengths, computations are roughly equivalent.
• Hence for similar security ECC offers significant computational
advantages.
advantages

33. Discrete Log Problem Over ECC (ECDLP)
Discrete Log Problem Over ECC (ECDLP)
• Th ECDLP i i
The ECDLP is, given elements r and q of the group formed
l t d f th f d
over elliptic curve find a number k such that r = kq.
p
• Example:
– In the elliptic curve defined by y2 = x3 + 9x + 17, what is the
discrete log k of Q(4,5) to the base P(16,5) ?
– One way to find k is to compute multiples of P until Q is found
One way to find k is to compute multiples of P until Q is found.
– P = (16,5) 2P = (20,20) 3P = (14,14)....8P = (12,17) 9P = (4,5)
– Since, 9P = (4,5) = Q, the discrete log of Q is k = 9.
• In a real application, k would be large enough such that it
would be infeasible to determine k in this manner.

34. Advantages of ECC over other
Cryptosystem
• For RSA which depends on Integer
p p
Factorization, DSA which depends upon
Fermat’s little Theorem and Diffie‐Hellman
protocol which depends upon DLP
protocol which depends upon DLP
– time required to crack them grows
subexponentially (a√n) with the length of key
subexponentially (a ) with the length of key.
• For Elliptic Curve Discrete Log Problem
(ECDLP) the time required to crack it grows
fully exponentially an.
y p y

35. Industrial Advantages
Industrial Advantages
• ECC offers equivalent security with much
y
smaller key size.
• Practical advantages of ECC :
–F t
Faster
– Low power consumption
– Low memory usage
– Low CPU utilization
Low CPU utilization
– Benefits of over its competitors increases with
increase in the security needs.
increase in the security needs