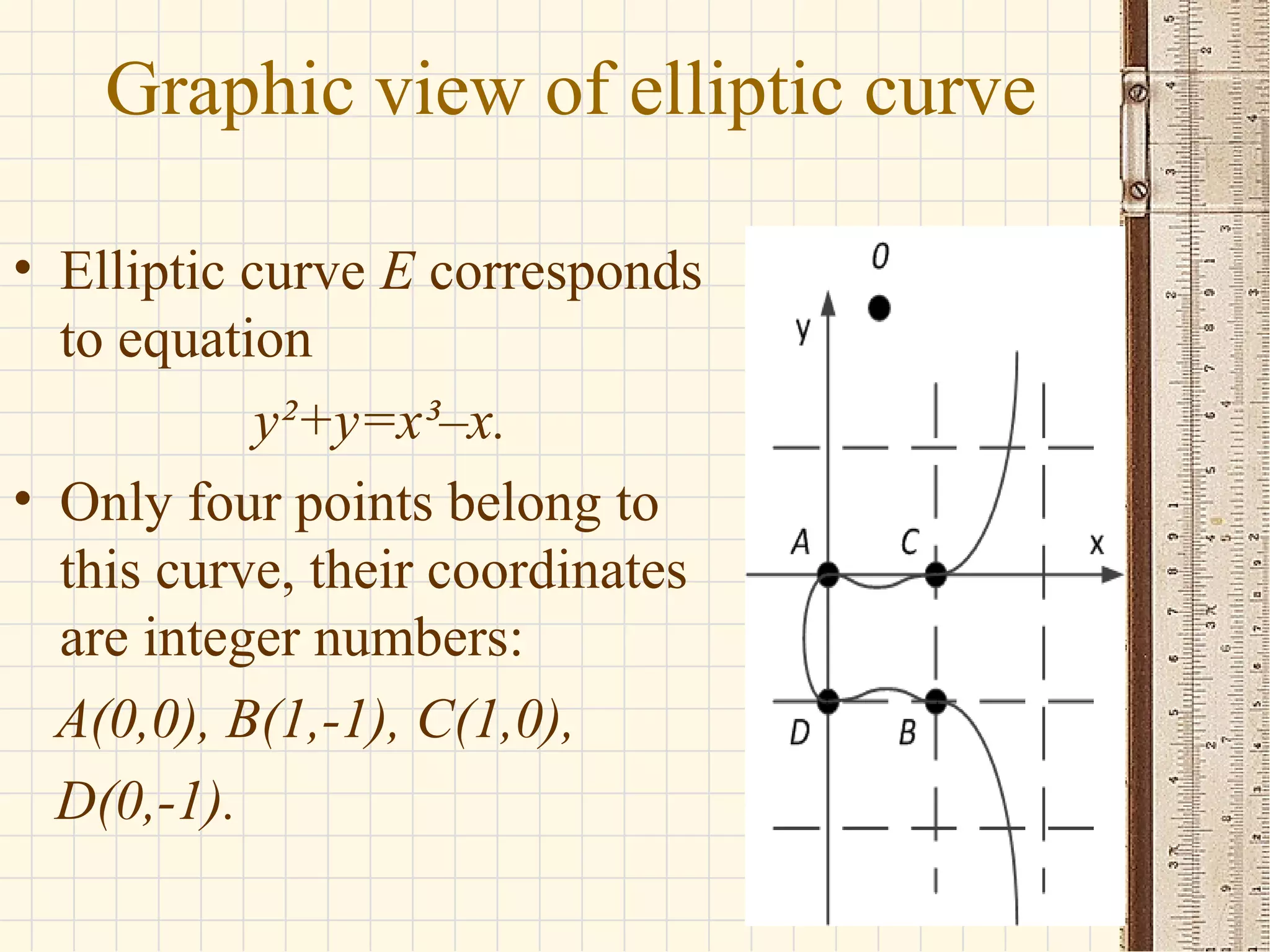
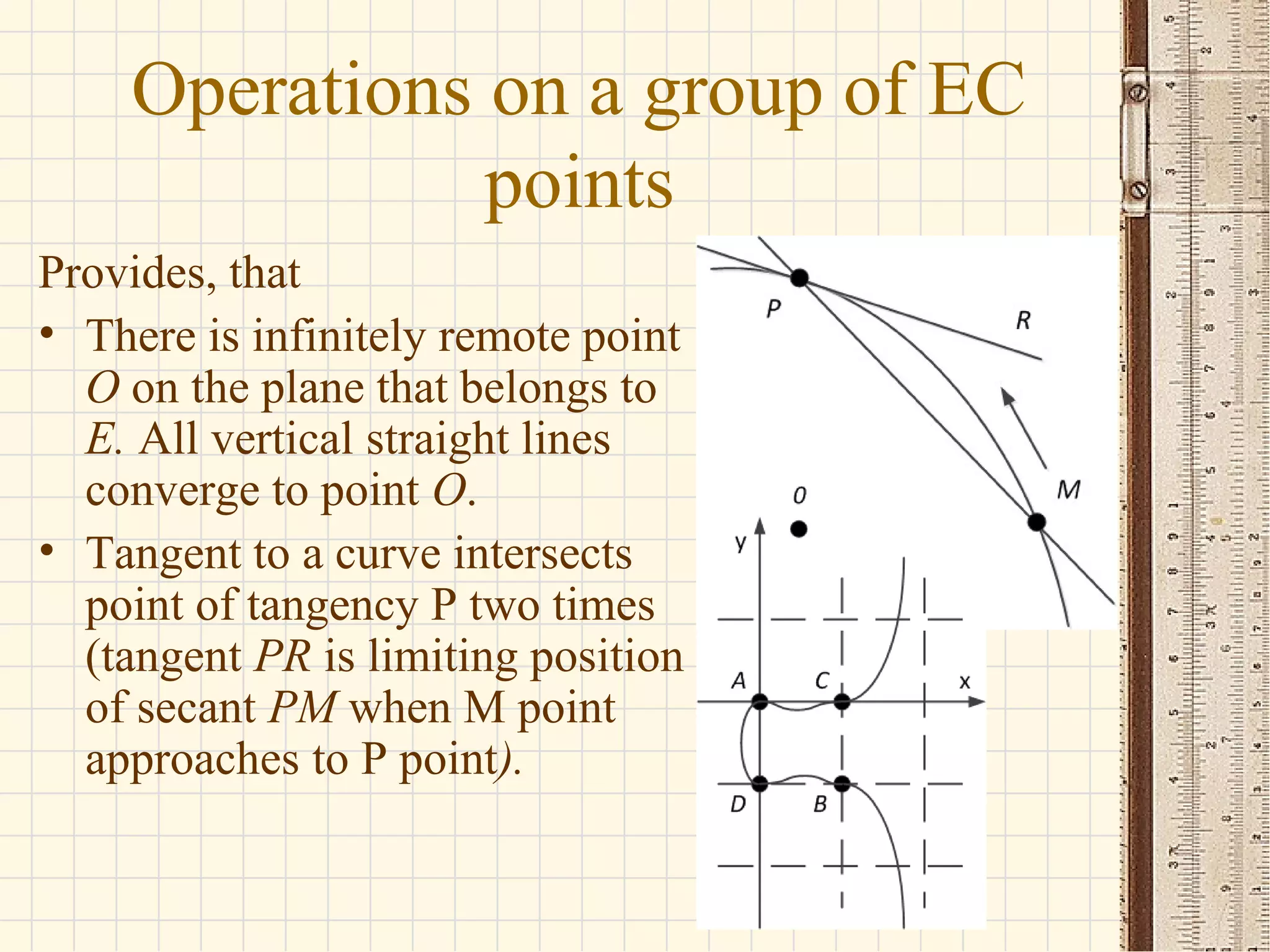
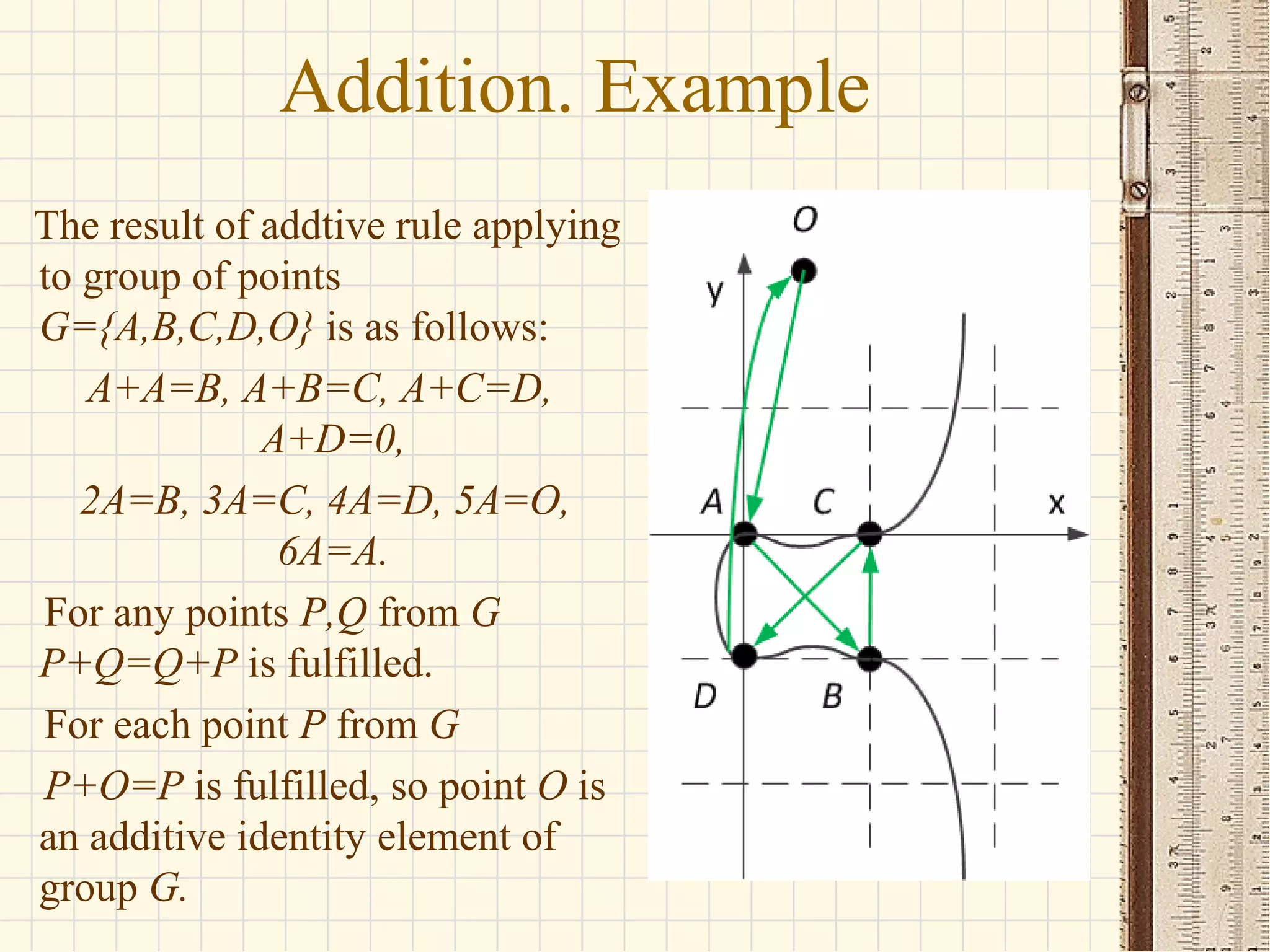
- Elliptic curves are algebraic structures used in cryptography and defined by cubic equations over finite fields. They form groups where the group operation is point addition. - A digital signature algorithm can be based on elliptic curves by using the discrete logarithm problem over elliptic curve groups. - The seminar discusses definitions of groups, elliptic curves, and their use in cryptography including defining the group operation of point addition on elliptic curves and calculating parameters like the group order.

1. Seminar #7
Information security
Elliptic curves
Kolybelnikov Alexander
kisttan@gmail.com

2. Agenda
• Group definition
• Elliptic curve definition
• Digital signature algorithm based on elliptic
curves

3. Terms and definitions

4. Group G is a set of elements a,b,c that have the following
properties:
• Operation of two variables is defined for G elements that is
written a┴b=c.
• Operation completeness: the result of an operation applying to
two group elements is another group element (completeness).
• For any three group elements associativity is fulfilled:
(a ┴ b) ┴ c = a ┴ (b ┴ c).
• There is a neutral element e in a group and for any group element
e ┴ a=a ┴ e=a is fulfilled.
• Each element a of G group has an inverse element a’:
a’ ┴ a=a ┴ a’=e.
Group definition

5. Group definition
• If commutative law is fulfilled for any G group elements a and
b (that means equation a ┴ b=b ┴ a is fulfilled) then G group is
Abelian.
• Order of group is a number of group elements. For complete
residue system GF(p) a set of all nonzero group elements is an
Abelian group of (p - 1) order.
• Some subset of G group is a subgroup if it meets all group
requirements (properties).
• Finite group that consists of its g element degrees 1, g, g², g³, …
is a cyclic group. The least integer number m: gm
=1 is an order
of g element.

6. General view of elliptic curve
• Generally EC is written
y2
+ axy + by = x3
+ cx2
+ dx + e
Cryptography restrictions:
• Elliptic curve shall not have singular points
that include self-intersections and cusp
points.

7. Graphic view of elliptic curve
• Elliptic curve E corresponds
to equation
y²+y=x³–x.
• Only four points belong to
this curve, their coordinates
are integer numbers:
A(0,0), B(1,-1), C(1,0),
D(0,-1).

8. Operations on a group of EC
points
Provides, that
• There is infinitely remote point
O on the plane that belongs to
E. All vertical straight lines
converge to point O.
• Tangent to a curve intersects
point of tangency P two times
(tangent PR is limiting position
of secant PM when M point
approaches to P point).

9. Addition. Example
Additive rule for P and Q points:
1) Draw straight line across P and
Q points, S is an intersection
point of this straight line and E
curve;
2) Draw vertical straight line across
S point before intersection with E
curve at T point;
3) Required sum is equal to
P+Q=T.

10. Addition. Example
The result of addtive rule applying
to group of points
G={A,B,C,D,O} is as follows:
A+A=B, A+B=C, A+C=D,
A+D=0,
2A=B, 3A=C, 4A=D, 5A=O,
6A=A.
For any points P,Q from G
P+Q=Q+P is fulfilled.
For each point P from G
P+O=P is fulfilled, so point O is
an additive identity element of
group G.

11. EC on finite field
The following equation is used in real
cryptosystems:
Provides, then
2 3 3 2
, , ( ),4 27 0(mod ), 3y x ax b a b GF p a b p p= + + ∈ + ≠ >
1 1 2 2
( , ), ( , )P x y Q x y= = 3 3
( , ),P Q x y+ =
2
3 1 2
3 1 3 1
;
( ) ;
x x x
y x x y
λ
λ
= − −
= − −
2 1
2 1
2
1
1
, ;
3
, .
2
y y
если P Q
x x
x a
если P Q
y
λ
−
≠ −
= 
+ =


12. Curve parameters
• Order of elliptic curve is an order of elliptic
curve points group (a number of different
points on E including O point)
• For elliptic curve E on prime field Fp the
order m of curve points group depends on
field dimension that is defined by prime
number p according to inequality:
p+1-2√p≤m≤p+1+2√p

13. Curve parameters
• Each point P of elliptic curve on prime field E(Fp)
forms cyclic subgroup G of elliptic curve points
group
• Order of cyclic subgroup of elliptic curve points
(number of points in a subgroup) is an order of
point of elliptic curve
• Point P on EF(p) is a point of q order if
qP=O
q is the least natural number which this condition
holds for

14. Caclulatin group generator and
point groups for EC
• Shouf algorithm
• Shouf-Etkis-Atkin algorithm
• Number of group elements φ(m), m is
module of curve.

15. Thank you for your attention!