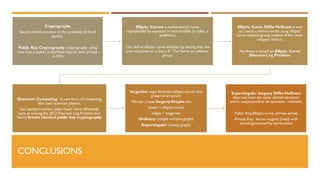
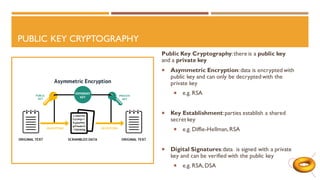
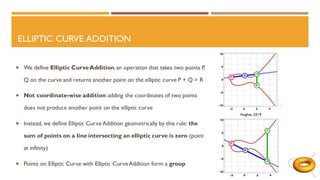
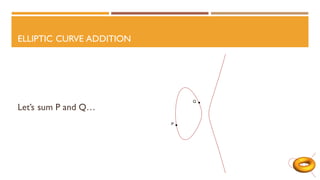
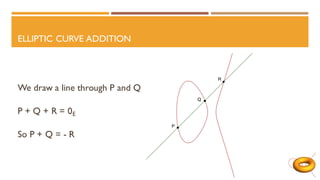
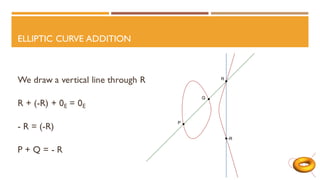
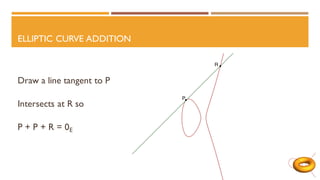
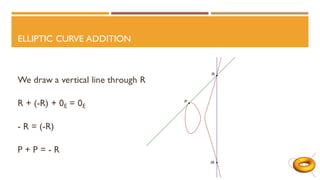
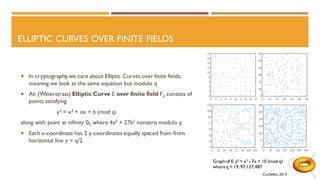
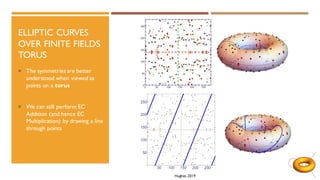
The document discusses elliptic curves in cryptography. It introduces elliptic curves, elliptic curve addition and multiplication, and how they can be used in public key cryptography. It describes elliptic curve Diffie-Hellman key exchange, where two parties establish a shared secret key over an elliptic curve. It also discusses how isogenies, which are rational maps between elliptic curves, can be used in post-quantum cryptographic protocols like the supersingular isogeny Diffie-Hellman key exchange. This protocol allows secure key exchange that is conjectured to be secure against both quantum and classical computers.








![ELLIPTIC CURVE MULTIPLICATION
We define elliptic curve multiplication-by-n map that takes a point P and produces a point [n]P = Q on the
elliptic curve by repeatedly adding P to itself
[n]P = P + P + … + P (n times)
Leuven, 2019](https://image.slidesharecdn.com/emilystamm-eccjan2020-200208225842/85/Elliptic-Curves-in-Cryptography-16-320.jpg)


![Alice
Bob
Alice Private Key
Integer a
Bob Private Key
Integer b
A B
K
Bob sends B to Alice
Alice sends A to Bob
Alice compute A = a[G]
Bob compute secret point
K = b[A]
Bob compute B = b[G]
Alice computes secret point
K = a[B]
Eve can only find K if she can solve
Elliptic Curve Discrete Log Problem:
Given A, G, find a such that A = a[G]
Eve
Public Key
• Prime q
• Elliptic Curve E: y2 = x3+ax+b
• Generator G of E(Fq)G
Elliptic Curve Diffie-Hellman](https://image.slidesharecdn.com/emilystamm-eccjan2020-200208225842/85/Elliptic-Curves-in-Cryptography-21-320.jpg)







![Alice
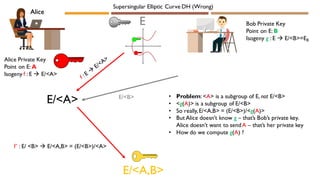
Alice Private Key
Integers m and n
Point A = [m]P +[n]Q
Isogeny f : E → E/<A>
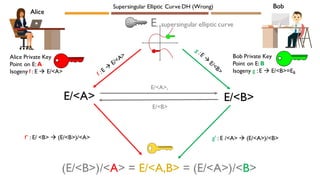
E/<A>
E/<A,B>
E
f’ : E/ <B> → E/<A,B> = (E/<B>)/< g( A)>
E/<B>, g(P), g(Q)
• Solution:Create private point A as a secret
linear combination of two public points P, Q
• Now Bob can send Alice g(P), g(Q)
• Which Alice can use to compute g(A) as
follows:
• g(A) = g(mP + nQ) = [m]g(P)+ [n] g(Q)
because g preserves group structure
• Now Alice can get
• E/<A,B> = (E/<B>)/< g( A)>
Bob Private Key
Integers mB, nB
Point B = [mB]PB +[nB]QB
Isogeny g : E → E/<B>
Supersingular Elliptic Curve DH](https://image.slidesharecdn.com/emilystamm-eccjan2020-200208225842/85/Elliptic-Curves-in-Cryptography-33-320.jpg)
![Alice
Bob
E/<A> E/<B>
Velu’s Formula to get f’
f’ : E/ <B> → (E/<B>)/<g(A)>
E/<B>, PB, QB , g(P), g(Q)
E/<A>, P, Q, f(PB ), f(QB)
g' : E /<A> → (E/<A>)/<f(B)>
Alice Private Key
Integers m and n
Point A = [m]P +[n]Q
Isogeny f : E → E/<A>
Bob Private Key
Integers mB, nB
Point B = [mB]PB +[nB]QB
Isogeny g : E → E/<B>
(E/<B>)/<g(A)> = E/<A,B> = (E/<A>)/<f(B)>
E, supersingular elliptic curve
E/<B> E/<A>
Supersingular Elliptic Curve DH](https://image.slidesharecdn.com/emilystamm-eccjan2020-200208225842/85/Elliptic-Curves-in-Cryptography-34-320.jpg)
![Alice
Bob
Alice Private Key
Integers mA, nA
Point A = [mA]PA +[nA]QA
Isogeny f : E → E/<A>=EA
Alice sends curve EA and points RA,SA
Bob compute new points on EB
RB = g(PA) and SB= g(QA)
Eve
Supersingular Isogeny Diffie-Hellman
Shared Secret Key K
K = j-invariant of E/<A,B>
Alice compute new isogeny with
kernel = <A,B>
E → EB/ <g(A)> = E/<A,B>
Eve can only find K if she can
compute g(A) or f(B) which she can
get g or f she can find the isogeny
between E and EA or EB
• Primes lA, lB, and p = lA
d lB
e f + 1
• Supersingular Elliptic Curve E over Fq, q = p2
• Points PA, QA (basis for lA
d torsion subgroup)
• Points PB, QB (basis for lB
e torsion subgroup)
Bob Private Key
Integers mB, nB
Point B = [mB]PB +[nB]QB
Isogeny g : E → E/<B>=EB
Alice compute new points on EA
RA = f(PB) and SA= f(QB)
Bob sends curve EB and points RB, SB
Bob compute new isogeny with
kernel = <A,B>
E → EA/ <f(B)> = E/<A,B>
Shared Secret Key K
K = j-invariant of E/<A,B>
Public Key](https://image.slidesharecdn.com/emilystamm-eccjan2020-200208225842/85/Elliptic-Curves-in-Cryptography-35-320.jpg)