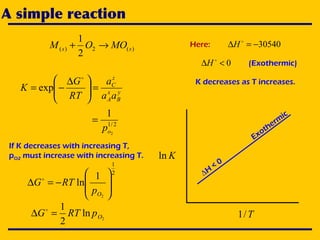
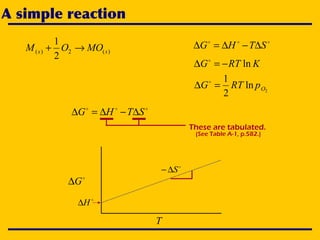
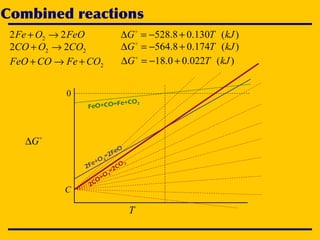
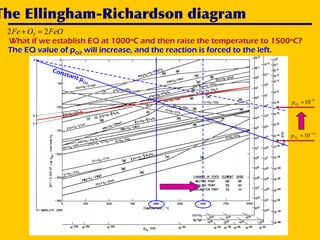
1. The document discusses thermodynamics and Ellingham diagrams for analyzing chemical reaction equilibria. It covers concepts like Gibbs free energy, equilibrium constants, and the temperature dependence of reactions. 2. An Ellingham diagram graphs the standard Gibbs free energy of formation of metal oxides as a function of temperature. This allows analyzing the stability of metals and oxides under different oxygen partial pressures and temperatures. 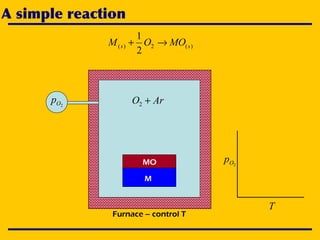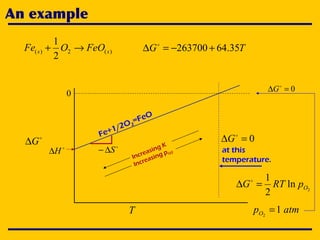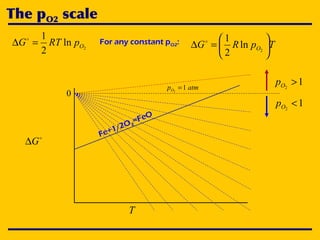3. The document uses the iron-oxygen reaction to illustrate how the equilibrium oxygen partial pressure increases with temperature according to the Ellingham diagram in order to maintain equilibrium.

1. Thermodynamics in Materials Engineering
Mat E 212 - Course Notes
R. E. Napolitano
Department of Materials Science & Engineering
Iowa State University
Reaction Equilibria
and an introduction to Ellingham Diagrams

2. A simple chemical reaction
CBA 2→+
State I
1A 1B
State II
2CCnBnAn CBA ++
Intermediate state
III GGG −=∆ 

BAC GGG −−= 2
Reaction coordinate
An
Bn
Cn
1
1
0
0
0
2
AB nn =
BAC nnn −−= 2
An22 −=
( )An−= 12
An
An
( )An−12
CCBBAA nnnG µµµ ++=
( ) CABAAA nnn µµµ −++= 12
For any intermediate state:

3. Consider only the mixing of A and B
State I
1A 1B
CBA 2→+
State II
2CCnBnAn CBA ++
Intermediate state
III GGG −=∆ 

BAC GGG −−= 2
0
0
2
AB nn =
BAC nnn −−= 2
An22 −=
( )An−= 12
An
An
( )An−12
CCBBAA nnnG µµµ ++=
( ) CABAAA nnn µµµ −++= 12
Reaction coordinate
An
Bn
Cn
1
1
0
For any intermediate state:

4. XB
G
Consider only the mixing of A and B
State I
1A 1B

AG

BG
For 1 mole A
and 1 mole B
(MIXED)
A+B
IG

BBAA GXGX +
(UNMIXED)
A B For 1 mole A
and 1 mole B
( )BBAABBAA XXXXRTGXGX lnln +++= 
mixBBAA STGXGX ∆−+ 

5. Gibbs free energy along reaction coordinate
State I State II
CBA 2→+
1A 1B 2CCnBnAn CBA ++
Intermediate state
III GGG −=∆ 

BAC GGG −−= 2
Reaction coordinate

AG

BG
mixed
A+B
IGA B 
CCBBAA GnGnGn ++
CCBBAA nnn µµµ ++

CII GG 2=
Equilibrium State
0=
∂
∂
An
G

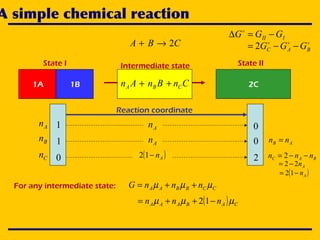
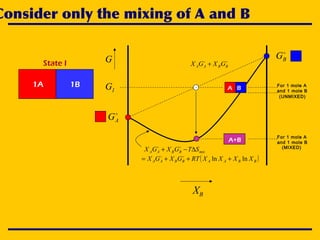
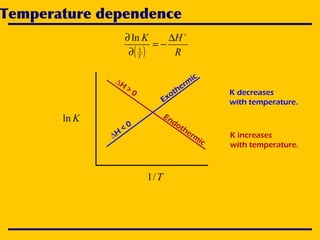
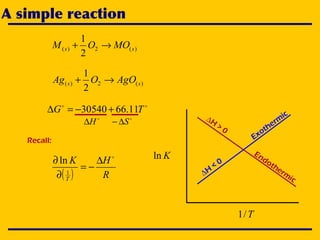
6. A simple chemical reaction
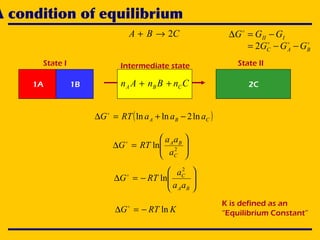
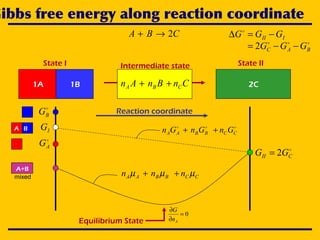
State I State II
CBA 2→+
1A 1B 2CCnBnAn CBA ++
Intermediate state
III GGG −=∆ 

BAC GGG −−= 2
( ) CABAAA nnn µµµ −++= 12CCBBAA nnnG µµµ ++=
Recall: iii aRTG ln+= 
µ
( ) ( ) ( )( )CCABBAAAA aRTGnaRTGnaRTGnG ln12lnln +−++++= 
( ) ( )[ ]CABAAACABAAA anananRTGnGnGn ln12lnln12 −+++−++= 
( ) 0ln2lnln2 =−++−+=
∂
∂
CBACBA
A
aaaRTGGG
n
G 
Find
minimum
along
reaction
coordinate: 
G∆−
( )CBA aaaRTG ln2lnln −+=∆ 

7. A condition of equilibrium
State I State II
CBA 2→+
1A 1B 2CCnBnAn CBA ++
Intermediate state
III GGG −=∆ 

BAC GGG −−= 2
( )CBA aaaRTG ln2lnln −+=∆ 






=∆ 2
ln
C
BA
a
aa
RTG






−=∆
BA
C
aa
a
RTG
2
ln
KRTG ln−=∆  K is defined as an
“Equilibrium Constant”

8. Temperature dependence
KRTG ln−=∆ 





 ∆
−=
RT
G
K

exp

STHG ∆−∆=∆Note that:


S
T
H
T
G
∆−
∆
=
∆
2
T
H
T
G
T

∆
−=




 ∆
∂
∂
( ) 2
ln
T
H
KR
T

∆
−=−
∂
∂
2
ln
RT
H
T
K 
∆
=
∂
∂
( )


H
T
G
T
∆=




 ∆
∂
∂
1
( )
( ) 
HKR
T
∆=−
∂
∂
ln1
( ) R
HK
T

∆
−=
∂
∂
1
ln

9. Temperature dependence
( ) R
HK
T

∆
−=
∂
∂
1
ln
Kln
T/1
Endotherm
ic
Exotherm
ic∆H
> 0
∆H
< 0
K increases
with temperature.
K decreases
with temperature.

10. A simple reaction
)(2)(
2
1
ss MOOM →+
ArO +2
MO
M
Furnace – control T
2Op
2Op
T

11. A simple reaction
)(2)(
2
1
ss MOOM →+

TG 11.6630540 +−=∆

S∆−
)(2)(
2
1
ss AgOOAg →+

H∆
( ) R
HK
T

∆
−=
∂
∂
1
ln
Recall:
Kln
T/1
Endotherm
ic
Exotherm
ic∆H
> 0
∆H
< 0

12. A simple reaction
Kln
T/1
Exotherm
ic
∆H
< 0
Here: 30540−=∆ 
H
0<∆ 
H (Exothermic)
K decreases as T increases.
)(2)(
2
1
ss MOOM →+
y
B
x
A
z
C
aa
a
RT
G
K =




 ∆
−=

exp
2/1
2
1
op
=
If K decreases with increasing T,
pO2 must increase with increasing T.
2
1
2
1
ln








−=∆
Op
RTG
2
ln
2
1
OpRTG =∆ 

13. A simple reaction
)(2)(
2
1
ss MOOM →+

STHG ∆−∆=∆
2
ln
2
1
OpRTG =∆ 
KRTG ln−=∆ 

STHG ∆−∆=∆
These are tabulated.
(See Table A-1, p.582.)

G∆
T

H∆

S∆−

14. An example
)(2)(
2
1
ss FeOOFe →+ TG 35.64263700 +−=∆ 

H∆

S∆−

G∆
T
Fe+1/2O2
=FeO
0=∆ 
G
at this
temperature.Increasing K
Increasing pO2
2
ln
2
1
OpRTG =∆ 
atmpO 12
=
0=∆ 
G
0

15. The pO2 scale

G∆
T
Fe+1/2O2
=FeO
atmpO 12
=
0
For any constant pO2:
2
ln
2
1
OpRTG =∆ 
TpRG O 





=∆ 2
ln
2
1
12
<Op
12
>Op

16. Combined reactions
FeOOFe 22 2 →+ )(130.08.528 kJTG +−=∆ 
22 22 COOCO →+ )(174.08.564 kJTG +−=∆ 
2COFeCOFeO +→+ )(022.00.18 kJTG +−=∆ 

G∆
T
2Fe+O2
=2FeO
0
2CO+O2
=2CO 2
FeO+CO=Fe+CO2
C

17. The Ellingham-Richardson diagram
FeOOFe 22 2 =+ )(7.128400,527 JTG +−=∆ 
)(76.30052,126 calTG +−=∆ 

18. The Ellingham-Richardson diagram
FeOOFe 22 2 =+ )(7.128400,527 JTG +−=∆ 
)(76.30052,126 calTG +−=∆ 
KRTG ln−=∆ 





 ∆
−=
RT
G
K

exp
At T=1000ºC:
( )127376.30052,126 +−=∆ 
G
)/(895,86 molcal=





 ∆
==
RT
G
K
pO

exp
1
2






−
−
=
)1273)(/987.1(
/86895
exp
KmolKcal
molcal
15
1021.1 −
×=
2
2
2
OFe
FeO
aa
a
K =
2
1
Op
K =

19. The Ellingham-Richardson diagram
FeOOFe 22 2 =+ )(7.128400,527 JTG +−=∆ 
)(76.30052,126 calTG +−=∆ 
Constant pO2
15
102
−
≈Op

20. The Ellingham-Richardson diagram
Constant pO2
15
102
−
≈Op
9
102
−
≈Op
The EQ value of pO2 will increase, and the reaction is forced to the left.
What if we establish EQ at 1000ºC and then raise the temperature to 1500ºC?
FeOOFe 22 2 =+