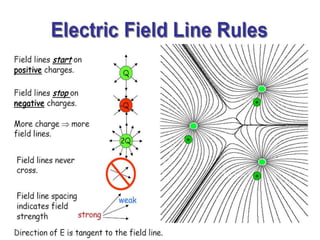
This document summarizes key concepts related to electric fields. It defines electric fields and their relationship to force. It then describes the electric field intensity and field patterns due to various charge distributions including point charges, multiple charges, infinite line charges, and infinite surface charges. It also covers Gauss's law relating electric field and charge distribution.

1. PREPARED BY
RAHUL SINHA-130280109107

2.  INTRODUCTION
 MAGNITUDE OF ELECTRIC FIELD INTENSITY
 ELECTRIC FIELD DUE TO POINT CHARGE
 PRINCIPLE OF SUPERPOSITION
 ELECTRIC FIELD DUE TO N CHARGES
 ELECTRIC FIELD LINES RULES & PATTERNS
 GAUSS’S LAW
 ELECTRIC FIELD DUE TO INFINITE LINE CHARGE
 ELECTRIC FIELD DUE TO INFINITE SURFACE
CHARGE

3.  In physics, the space
surrounding an electric charge
has a property called an
electric field.
 The electric field exerts a force
on other electrically charged
objects.
 The concept of an electric field
was introduced by Michel
Faraday.
Michael Faraday
(1791-1867)

4.  The magnitude of electric field intensity at any point in
electric field is given by force that would be
experienced by a unit positive charge placed at that
point.
UNIT: N/C OR V/M
F
E
Q


5.  The electric field at a point P due to a charge q is the
force acting on a test charge q0 at that point P,
divided by the charge q0 :
For a point charge q
0
0
( )
qq
q
F
E p
q

ˆ( )
4 ^ 2
q
q
E p r
r



6.  The total field at a point is the vector sum of the
individual component fields at the point.
 The field intensity of the charge Q1 at the point P is E1
and field due to charge Q2 is E2.
 The total field at P due to both charges is the vector sum
of E1 and E2.

7.  When there are n number of charges,the field due to
each point charge is given by,
4 ^ 2
r
Q
E a
r



8.  By the principle of superposition electric field due to n
number of charges is,
1 2
1 2
1 22 2 2
1 2
2
1
...
...
4 4 4
1
4
N
n
r r n
n
n
i
ri
i i
E E E E
QQ Q
E a a a
r r r
Q
E a
r
  
 
   
   
  




10.  For a positive charge electric field lines radiate
outwards.
 For a negative charge electric field lines point inwards.

11.  Gauss’s law: The electric field at any point in
space is proportional to the line density at that point.
Line density
s
DN
N
A
s
D

D

12.  Consider the field near a positive charge q.
 Then imagine a surface of radius r surrounding the
charge q.
 E is proportional tos
0
E
N
E
A
N
E
A
s

D
D
D

D
Gaussian Surface
Radius r
r

13.  The proportionality constant for line density is known
as the permittivity and is given by
 Recalling the relationship with line density we have:
2
12
0 2
1
8.85 10
4 .
C
k N m

   
0
0
N
E
A
N E A
D

D
D  D

14.  Summing over the entire area A gives the total lines as
 If we represent q as net charge then
0N EA
Gauss’s law: The net number of electric field
lines crossing any closed surface in outward
direction is numerically equal to the net total
charge within that surface.
0
q
EA 


0N EA q   

15.  Consider the infinite line
charge is placed along the
z-axis.
 Consider the line charge as
axis of the cylinder in
cylindrical co ordinates
 The point where we desire
the field is in xy plane at
point P.

16.  Consider a small charge dQ on z-axis at point Q.
So,Vector from point P to Q
So , unit vector
l ldQ dl dz  
zR a za 
^ 2 ^ 2
z
R
a za
a
z






17.  Thus ,the diffrential electric field due to dQ is
04 ^ 2
R
dQ
dE a
R


04 ^ 2 ^ 2 ^ 2
za zadQ
dE
R z

 
 
     
04 ( ^ 2 ^ 2) ^ 2 ^ 2
zl
a zadz
dE
z z

  
 
      

18.  By solving above equation we get the equation of
electric field intensity due to infinite line charge
04 ( ^ 2 ^ 2) ^ (3 / 2)
l dz
dE a
z



 
 

 
02
l
RE a
R





19.  Consider the infinite sheet
with charge density given in
the xy-plane.
 The point where we desire the
electric field is on z-axis refer
fig given.

20.  The vector from Q to P and its unit vector are given by,
 The electric field due to small charge dQ on the sheet is
given by,
^ 2 ^ 2
z
z
R
R a za
a za
a
z





  
 


04 ^ 2
R
dQ
dE a
R



21.  Putting the value of R we get the equation
 The total electric field is obtained by integrating dE we
get,
04 ( ^ 2 ^ 2) ^ 2 ^ 2
zs
a zad d
dE
z z
   
  
  
  
    
2
00 0
( )
4 ( ^ 2 ^ 2) ^ 3/ 2
s
z
d d
E za
z

   
 


  

22.  By solving the above equation we get the electric field
intensity due to infinite sheet charge,
02
s
nE a




23.  Magnitude of electric field
 Electric field due to point charge
ˆ( )
4 ^ 2
q
q
E p r
r


F
E
Q


24.  GAUSS’S LAW
 Electric field due to infinite line charge
 Electric field due to infinite surface charge
02
s
nE a



02
l
RE a
R




0
q
EA 



25.  http://en.wikipedia.org/wiki/Electric_field
 http://en.wikipedia.org/wiki/Gauss%27s_law
 http://en.wikipedia.org/wiki/Field_line

26. THANK YOU