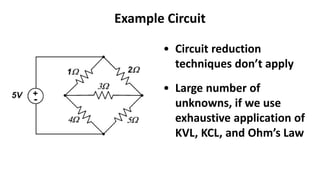
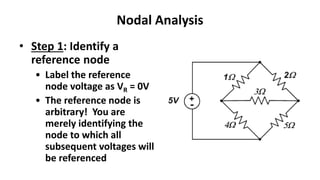
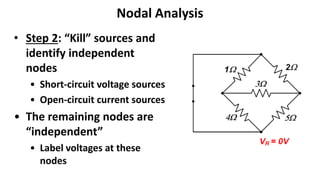
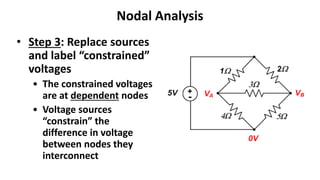
The document discusses nodal analysis techniques for circuit analysis. It begins with an overview of circuit analysis methods introduced so far like Ohm's Law, Kirchoff's Laws, and circuit reduction. It then explains that nodal analysis and mesh analysis provide rigorous ways to define a small set of unknowns and write governing equations in terms of these unknowns. The document proceeds to provide an overview of nodal analysis techniques like identifying independent nodes and writing KCL equations at each node. It works through an example circuit applying the nodal analysis steps and provides shortcuts that can be taken.

1. Lecture 7
•Review:
•Circuit techniques to date
•Overview of Nodal and Mesh analysis
•Nodal Analysis
•Related educational modules:
–Sections 1.6.0, 1.6.1

2. Circuit analysis methods introduced so far
• Voltage-current relations:
• Ohm’s Law
• Kirchoff’s Current Law (KCL)
• Kirchoff’s Voltage Law (KVL)
• Circuit Reduction
• But circuit reduction is just a way of applying Ohm’s Law,
KCL, and KVL to simplify the analysis by reducing the
number of unknowns!

3. Example Circuit
• Circuit reduction
techniques don’t apply
• Large number of
unknowns, if we use
exhaustive application of
KVL, KCL, and Ohm’s Law

4. Two new analysis techniques
• Next:
• Nodal Analysis
• Mesh Analysis
• Nodal analysis and mesh analysis provide rigorous
ways to define a (relatively small) set of unknowns
and write the circuit governing equations in terms
of these unknowns

5. Nodal analysis – overview
• Identify independent nodes
• The voltages at these nodes are the node voltages
• Use Ohm’s Law to write KCL at each independent node
in terms of the node voltages
• Solve these equations to determine the node voltages
• Any desired circuit parameter can be determined from
the node voltages

6. Mesh analysis – overview
• Identify mesh loops
• The currents around these loops are the mesh currents
• Use Ohm’s Law to write KVL around each loop in terms
of the mesh currents
• Solve these equations to determine the mesh currents
• Any desired circuit parameter can be determined from
the mesh currents

7. Important observation
• Nodal analysis and mesh analysis are not
fundamentally “new” analysis techniques
• We are still applying KVL, KCL, and Ohm’s Law!
• Nodal and mesh analysis simply allow us to identify a
reduced set of unknowns which completely characterize
the circuit  we can write and solve fewer equations to
simplify our analysis!

8. Nodal Analysis
• We will illustrate the nodal analysis technique in
the context of an example circuit:

9. Nodal Analysis
• Step 1: Identify a
reference node
• Label the reference
node voltage as VR = 0V
• The reference node is
arbitrary! You are
merely identifying the
node to which all
subsequent voltages will
be referenced

10. Nodal Analysis
• Step 2: “Kill” sources and
identify independent
nodes
• Short-circuit voltage sources
• Open-circuit current sources
• The remaining nodes are
“independent”
• Label voltages at these
nodes

11. Nodal Analysis
• Step 3: Replace sources
and label “constrained”
voltages
• The constrained voltages
are at dependent nodes
• Voltage sources
“constrain” the
difference in voltage
between nodes they
interconnect

12. Nodal Analysis
• Step 4: Apply KCL at
each independent
node
•

13. Nodal Analysis
• Step 5: Use Ohm’s Law
to write the KCL
equations in terms of
node voltages
–

14. Nodal Analysis
• Step 5: continued

15. Nodal Analysis
• Step 6: Solve the
system of equations
to determine the
node voltages
• The node voltages
can be used to
determine any other
desired parameter in
the circuit

16. Nodal Analysis – checking results
• Checking results in step 5:
• In general, in the equation for node “X”, the
multiplicative factor on the node voltage VX will be the
sum of the conductances at node “X”
• The multiplicative factors on all other node voltages in
the equation will be the negative of the conductances
between node “X” and the respective node voltage

17. Nodal Analysis – checking results

18. Nodal Analysis – shortcuts
• It is common to combine steps 4 and 5
• Apply KCL and Ohm’s Law simultaneously
• You can, if you wish, choose your current directions
independently each time you apply KCL
• For example, you can assume that all currents are leaving
the node, each time you apply KCL

19. Shortcuts applied to our example
• • Previous Results:

20. Nodal analysis – example 2
• Use nodal analysis to find i in the circuit below

21. Example 2 – continued

22. Example 2 – What if we mis-identify independent
nodes?

23. Nodal analysis – example 3
• Use nodal analysis to determine v in the circuit below

24. Example 3 – Alternate reference node