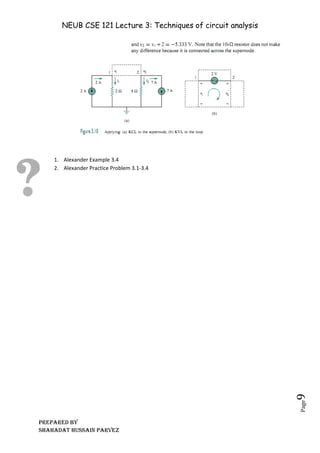
The document discusses advanced techniques for circuit analysis, particularly nodal and mesh analysis, which simplify the analysis of larger circuits beyond basic laws like KCL, KVL, and Ohm’s Law. Nodal analysis focuses on calculating node voltages by selecting a reference node and applying KCL, while mesh analysis uses mesh currents and KVL to find unknown currents in planar circuits. Each technique has defined steps for formulating and solving simultaneous equations to derive the desired electrical variables.