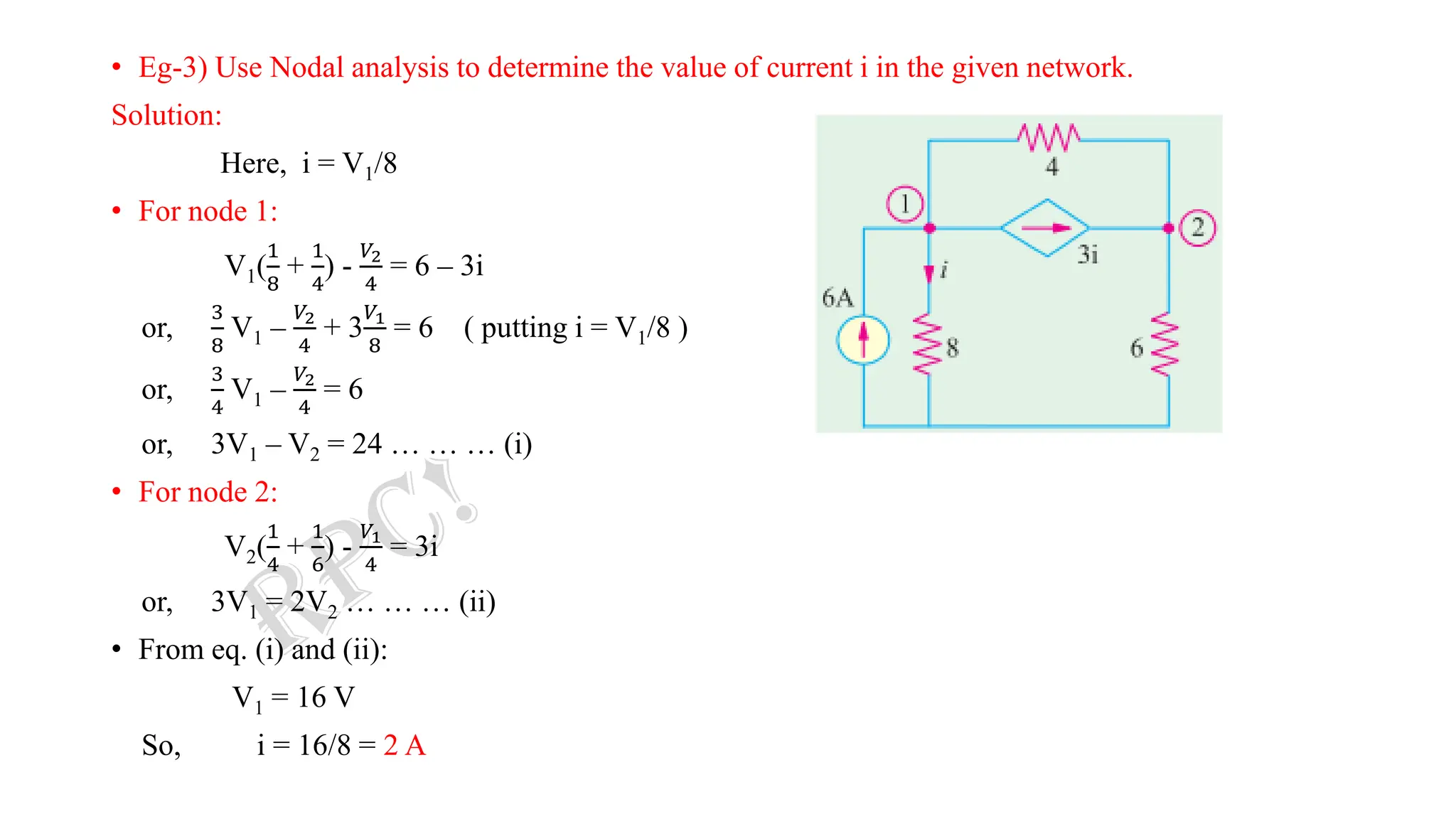
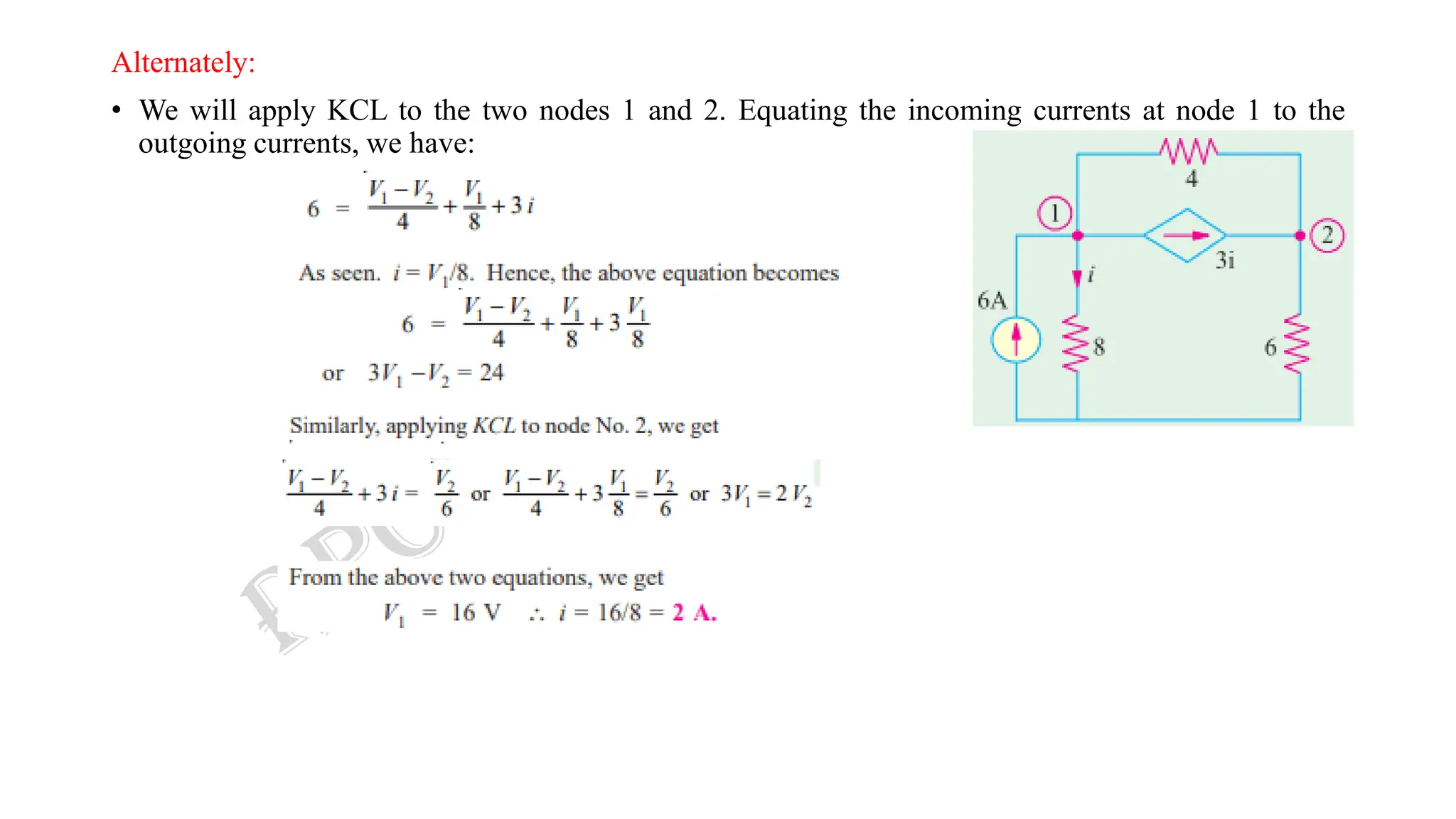
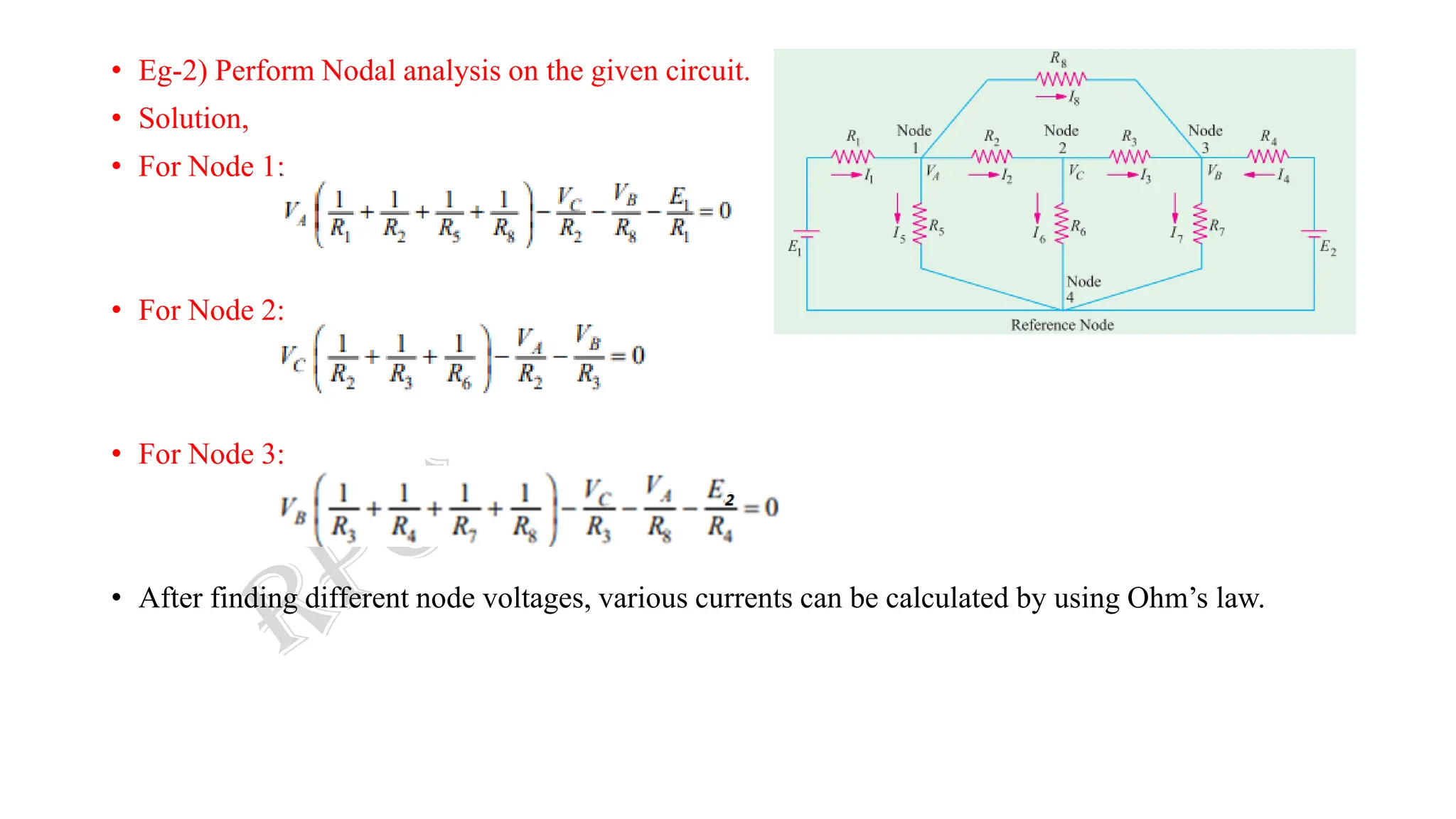
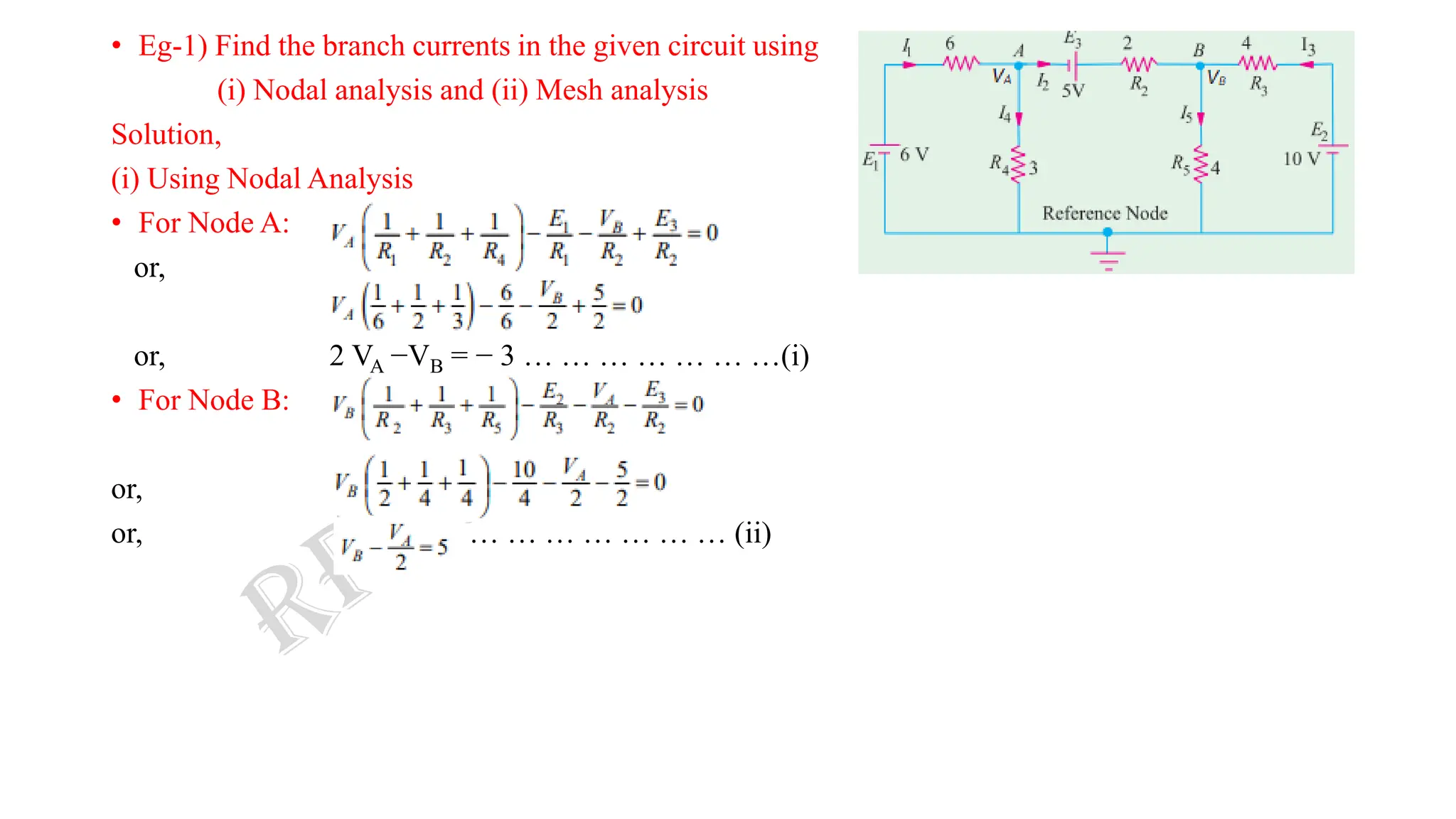
Nodal analysis is a technique to analyze electrical circuits using Kirchhoff's Current Law (KCL). It involves writing nodal equations for each node in the circuit where three or more branches meet. The document discusses nodal analysis through examples. It explains how to write nodal equations for each node by equating the sum of incoming currents to the sum of outgoing currents. The equations relate the node voltages to branch currents using Ohm's law. Solving the system of nodal equations determines the node voltages and allows calculating branch currents. The document also discusses applying nodal analysis to circuits with current sources.

1. NODAL ANALYSIS

2. NODAL ANALYSIS:
• Unlike mesh analysis (which uses KVL), Nodal analysis uses KCL.
• Minimum number of equations are required to determine unknown quantities.
• Every junction in a network where three or more branches meet is regarded as NODE, one of
which is regarded as a reference or 0 potential node.
• If there are ‘n’ number of nodes, the number of equations is (n-1).
• It is particularly suited for networks having many parallel circuits with common ground connected
such as electronic circuits.

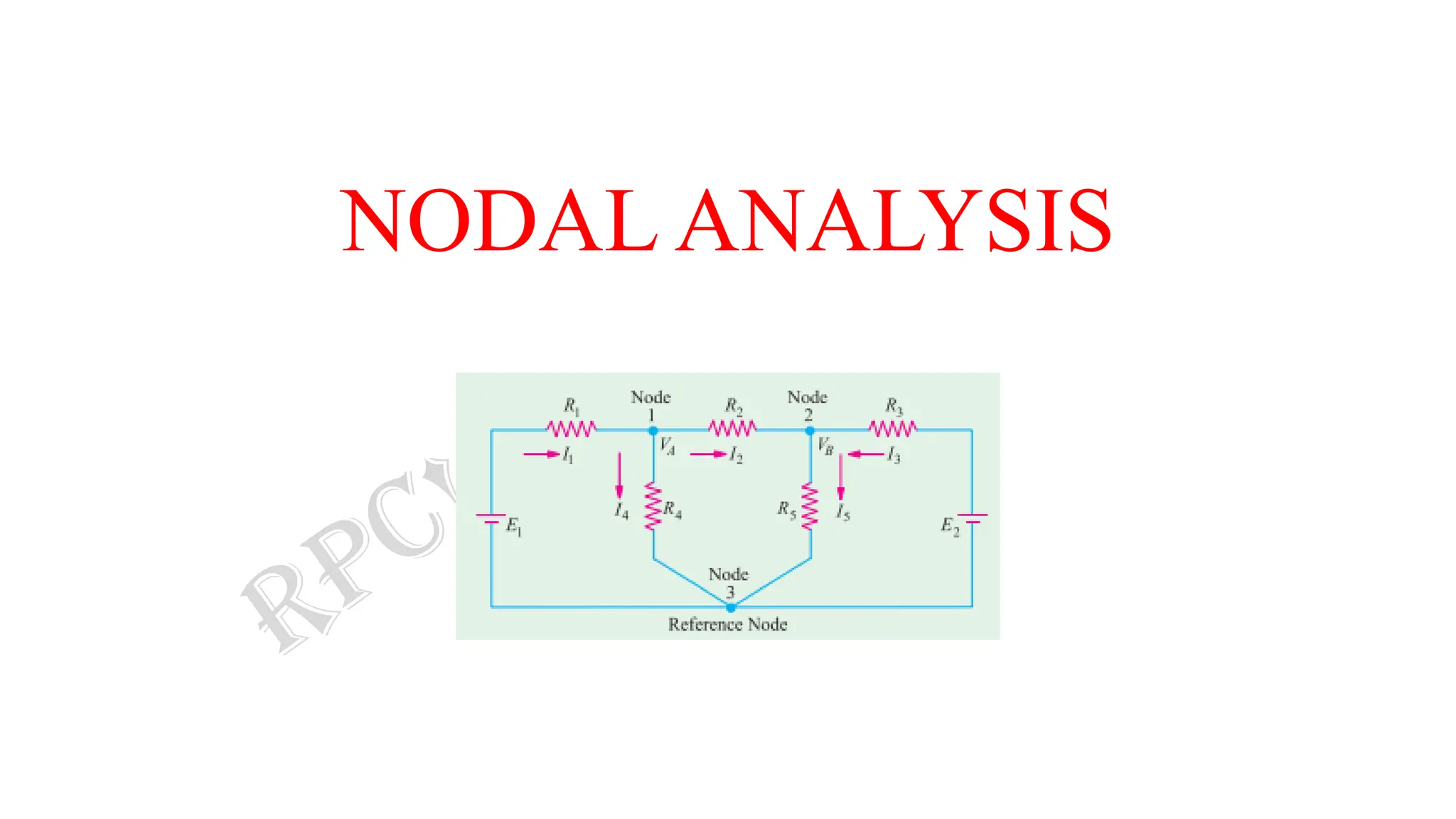
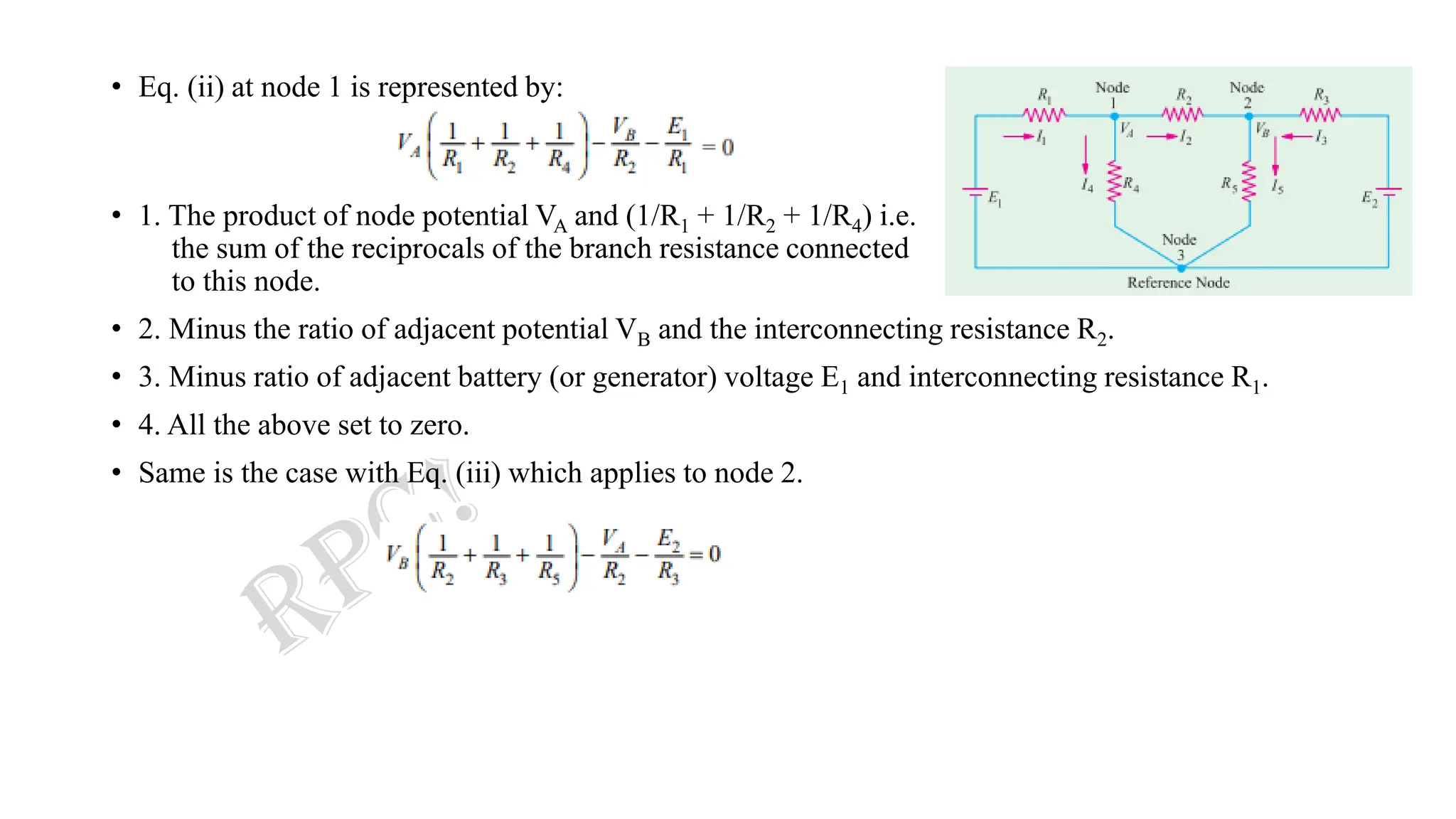
3. CASE I:
• Consider the circuit of figure below which has three nodes.
• One of these i.e. node 3 has been taken in as the reference
node.
• VA represents the potential of node 1 with reference to the
reference node 3.
• Similarly, VB is the potential difference between node 2 and node 3.
• Let the current directions, which have been chosen arbitrary, be as shown.
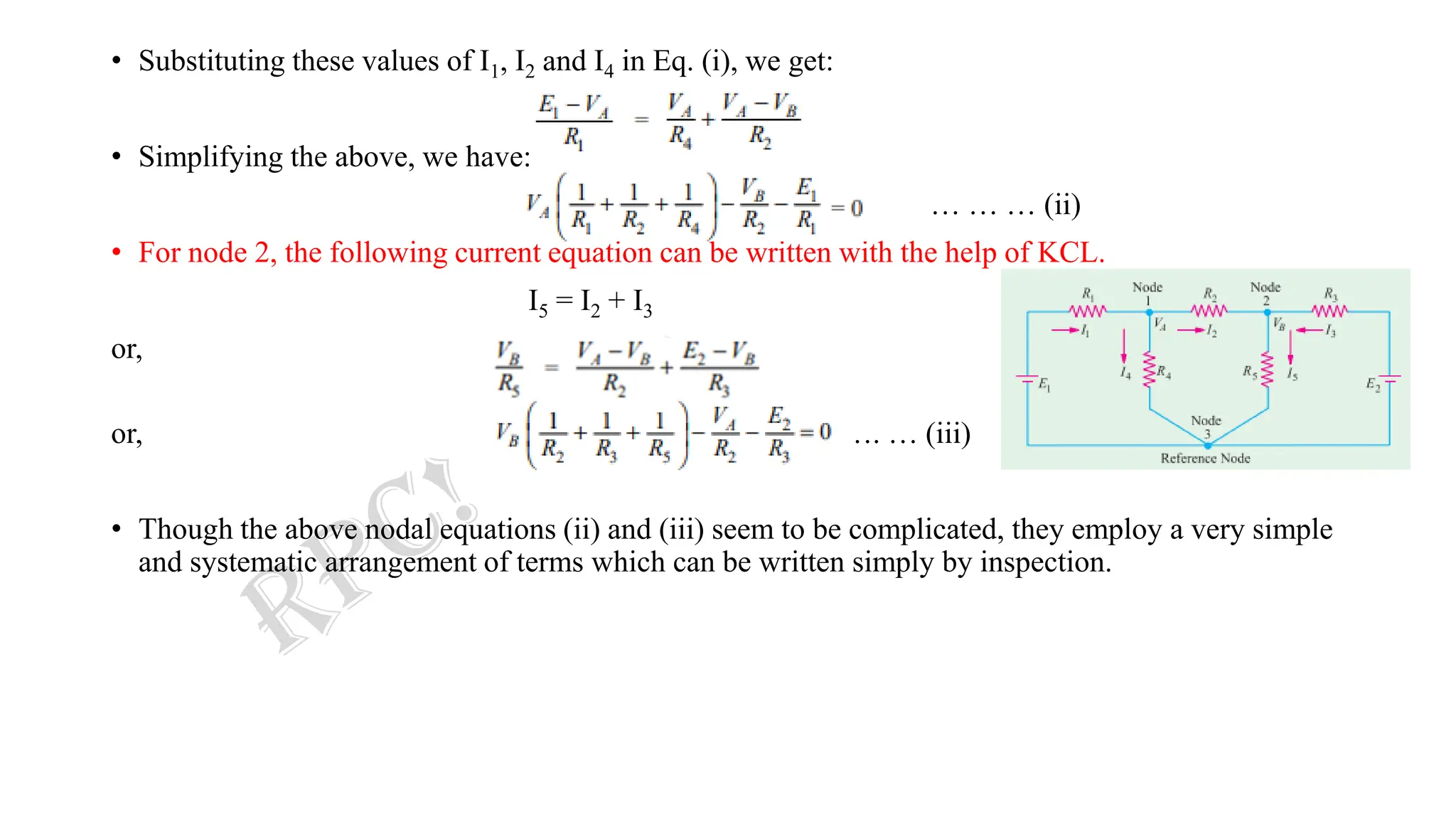
• For node 1, the following current equation can be written with the help of KCL.
I1 = I4 + I2 ... … … (i)
Now, I1R1 = E1 −VA [Applying KVL in Mesh (i)]
∴ I1 = (E1 −VA) /R1
And, I4 = VA/R4
Also, I2R2 = VA −VB ( since, VA > VB) [Applying KVL in Mesh (ii)]
∴ I2 = (VA −VB) /R2

4. • Substituting these values of I1, I2 and I4 in Eq. (i), we get:
• Simplifying the above, we have:
… … … (ii)
• For node 2, the following current equation can be written with the help of KCL.
I5 = I2 + I3
or,
or, …. … (iii)
• Though the above nodal equations (ii) and (iii) seem to be complicated, they employ a very simple
and systematic arrangement of terms which can be written simply by inspection.

5. • Eq. (ii) at node 1 is represented by:
• 1. The product of node potential VA and (1/R1 + 1/R2 + 1/R4) i.e.
the sum of the reciprocals of the branch resistance connected
to this node.
• 2. Minus the ratio of adjacent potential VB and the interconnecting resistance R2.
• 3. Minus ratio of adjacent battery (or generator) voltage E1 and interconnecting resistance R1.
• 4. All the above set to zero.
• Same is the case with Eq. (iii) which applies to node 2.

6. • Eg-2) Perform Nodal analysis on the given circuit.
• Solution,
• For Node 1:
• For Node 2:
• For Node 3:
• After finding different node voltages, various currents can be calculated by using Ohm’s law.

7. CASE II:
• Now, consider the case when a third battery of emf E3 is connected between nodes 1 and 2 as
shown in Figure.
• It must be noted that as we travel from node 1 to node 2,
we go from the −ve terminal of E3 to its +ve terminal.
Hence, according to the sign convention, E3 must be taken
as positive.
• However, if we travel from node 2 to node 1, we go from the
+ve to the −ve terminal of E3. Hence, when viewed from
node 2, E3 is taken negative.
• For node 1:
I1 −I4 −I2 = 0
Or, I1 = I4 + I2 − as per KCL
Now,
So,
… … …(i)

8. • For node 2:
I2 + I3 −I5 = 0
Or, I2 + I3 = I5 − as per KCL
Now,
So,
... ... ... (ii)
• As seen, the additional terms is −E3/R2 (and not + E3/R2) because as viewed from this node, E3
represents a fall in potential.
• It is worth repeating that the additional term in the above Eq. (i) and (ii) can be either +E3/R2 or
−E3/R2 depending on whether it represents a rise or fall of potential when viewed from the node
under consideration.

9. • Eg-1) Find the branch currents in the given circuit using
(i) Nodal analysis and (ii) Mesh analysis
Solution,
(i) Using Nodal Analysis
• For Node A:
or,
or, 2 VA −VB = − 3 … … … … … … …(i)
• For Node B:
or,
or, … … … … … … … (ii)

10. • From Eq. (i) and (ii), we get:
VA= 4/3 V and VB = 17/3 V
So,
And,
And,
And,
And,

11. (ii) Using Mesh Analysis:
• Let the direction of flow of the three loop currents be as shown in the
circuit.
• For Mesh I (Loop ABFA) :
− 6I1 − 3(I1 −I2) + 6 = 0
or, 3I1 −I2 = 2 … … … (i)
• For Mesh II (Loop BCEFB) :
+ 5 − 2I2 − 4(I2 −I3) − 3 (I2 −I1) = 0
or, 3I1 − 9I2 + 4I3 = − 5 ... ... ... (ii)
• For Mesh III (Loop CDEC) :
− 4I3 − 10 − 4 (I3 −I2) = 0
or, 2I2 − 4I3 = 5 ... ... ... (iii)

12. • Now, we have:
3I1 −I2 = 2 … … … (i)
3I1 − 9I2 + 4I3 = − 5 ... ... ... (ii)
2I2 − 4I3 = 5 ... ... ... (iii)

13. • Eg-2) Using Node voltage method, find the current in the 3Ω resistance for the network shown in
given figure.
• Solution:
• As shown in the figure node 2 has been taken as the reference node.
We will now find the value of node voltage V1. Using Nodal analysis,
we get:
• The reason for adding the two battery voltages of 2 V and 4 V is
because they are connected in additive series.
• Simplifying above, we get V1 = 8/3 V.
• The current flowing through the 3 Ω resistance towards node 1 =

14. • Eg-3) Solve the node equations of the network in the given circuit and find the total power
consumed by the passive elements of the circuit.
• Solution
• The node equation for node 1 is:
• Similarly, for node 2, we have:
• Solving (i) and (ii), we get:
• Now,
• The passive elements of the network are its five resistances. Total power consumed by them is =
(5.75)2 × 1 + (3.5)2 × 0.5 + (9)2 × 1 + (9.25)2 × 1 + (5.5)2 × 2 = 266.25 W.

15. • Eg-4) Find the branch currents in the given circuit by using (i) nodal analysis and (ii) mesh analysis
• Solution:
• This is your class work. Do it now and HURRY UP!

16. CASE III: NODAL ANALYSIS WITH CURRENT SOURCES
• Consider the network of Fig.(a) which has two current sources and three nodes out of which 1 and
2 are independent ones whereas No. 3 is the reference node.
• The given circuit has been redrawn for ease of understanding and is shown in Fig.(b). The current
directions have been taken on the assumption that:
1. both V1 and V2 are positive with respect to the reference node. That is why their respective
currents flow from nodes 1 and 2 to node 3.
2. V1 is positive with respect to V2 because current has been shown flowing from node 1 to node
2.

17. • We will now apply KCL to each node and use Ohm’s law to express branch currents in terms of
node voltages and resistances.
• For Node 1:
I1 −I2 −I3 = 0
or, I1 = I2 + I3
Now,
So, … … … (i)
• For Node II:
I3 −I5 −I4 = 0
or, I3 = I5 + I4
So,
Now, ... ... ... (ii)

18. • The above two equations can also be written by simple inspection. For example, Eq. (i) is
represented by
1. product of potential V1 and (1/R1 + 1 /R3) i.e. sum of the reciprocals of the branch
resistances connected to this node.
2. minus the ratio of adjoining potential V2 and the interconnecting resistance R3.
3. all the above equated to the current supplied by the current source connected to this node. This
current is taken positive if flowing into the node and negative if flowing out of it.
• Same remarks apply to Eq. (ii) where I2 has been taken negative because it flows away from node
2.

19. • Eg-1) Use nodal analysis method to find currents in the various resistors of the circuit shown in
circuit.
Solution:
• The given circuit is redrawn in Fig.(b) with its
different nodes marked 1, 2, 3 and 4, the last one
being taken as the reference or datum node. The
different node-voltage equations are as under:
• For Node 1:
or, 11V1 − 5V2 −V3 = 280 … … … (i)
• For Node 2:
or, 5V1 − 17 V2 + 10 V3 = 0 … … … (ii)
• For Node 3:
or, V1 + 10 V2 − 13.5 V3 = 20 … … … (iii)

20. • 11V1 − 5V2 −V3 = 280 … (i),
5V1 − 17 V2 + 10 V3 = 0 … (ii)
V1 + 10 V2 − 13.5 V3 = 20 … (iii)
• The matrix form of the above three equations is:
So,

21. • It is obvious that all nodes are at a higher potential with respect to the datum node. The various
currents shown in Fig. can now be found easily:
• Here, V1 = 36 V
V2 = 20 V
V3 = 16 V
I1 = V1/2 = 36/2 = 18 A
I2 = (V1 −V2)/2 = (36 − 20)/2 = 8 A
I3 = (V1 −V3)/10 = (36 − 16)/10 = 2 A
• It is seen that total current, as expected, is 18 + 8 + 2 = 28 A
I4 = (V2 −V3)/1 = (20 − 16)/1 = 4 A
I5 = V2/5 = 20/5 = 4 A
I6 = V3/4 = 16/4 = 4 A

22. • Eg-2) Using nodal analysis, find the different branch currents in the circuit given below. All
branch conductances are in Siemens (i.e. mho).
Solution:
• First Node
V1 (1 + 2) −V2 × 1−V3 × 2 = − 2
or, 3V1 −V2 − 2V3 = − 2 … … ...(i)
• Second Node
V2 (1 + 4) −V1 × 1 = 5
or, V1 − 5V2 = − 5 … … …(ii)
• Third Node
V3 (2 + 3) −V1 × 2 = − 5
or, 2V1 − 5V3 = 5 … … ...(iii)

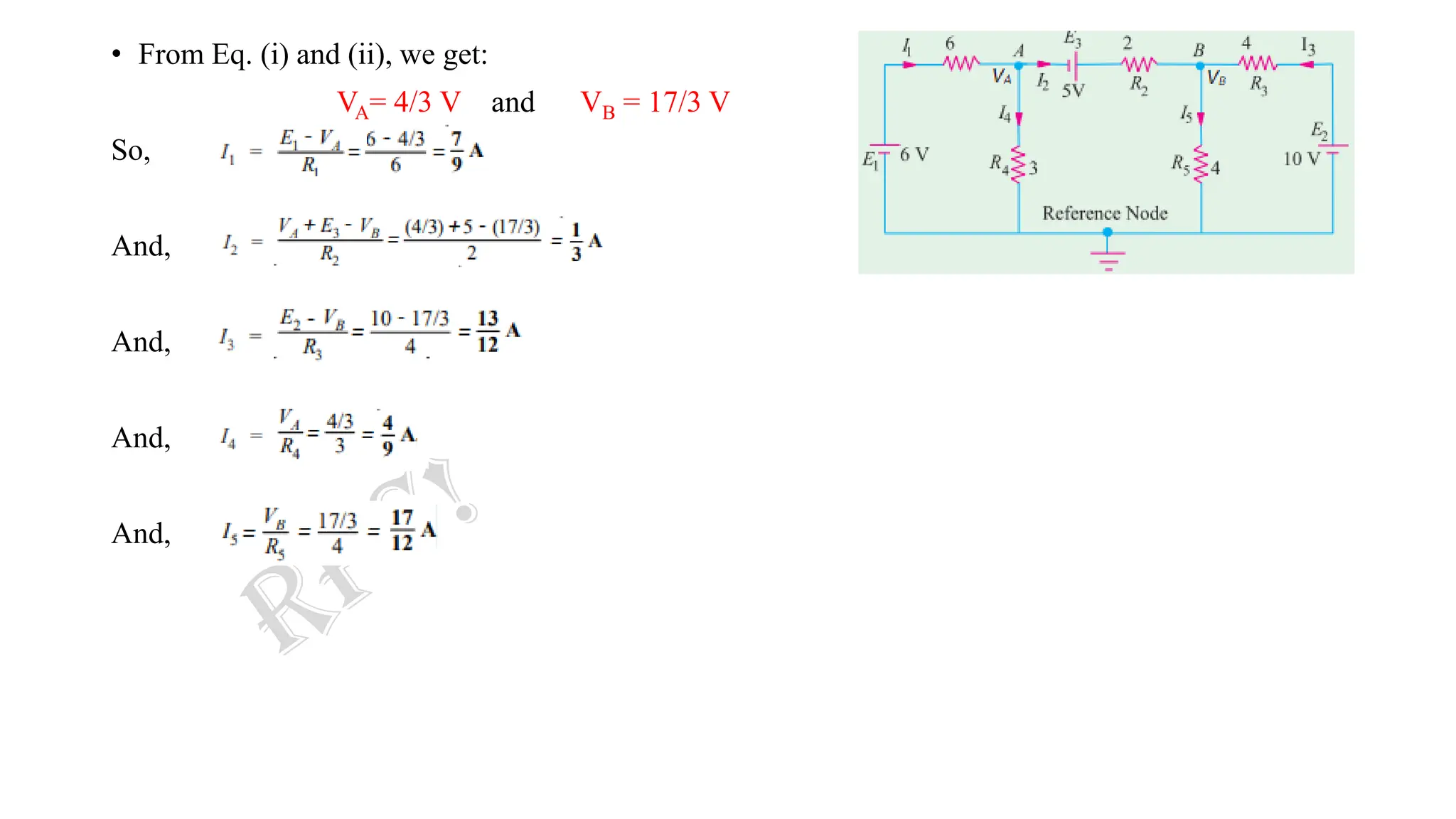
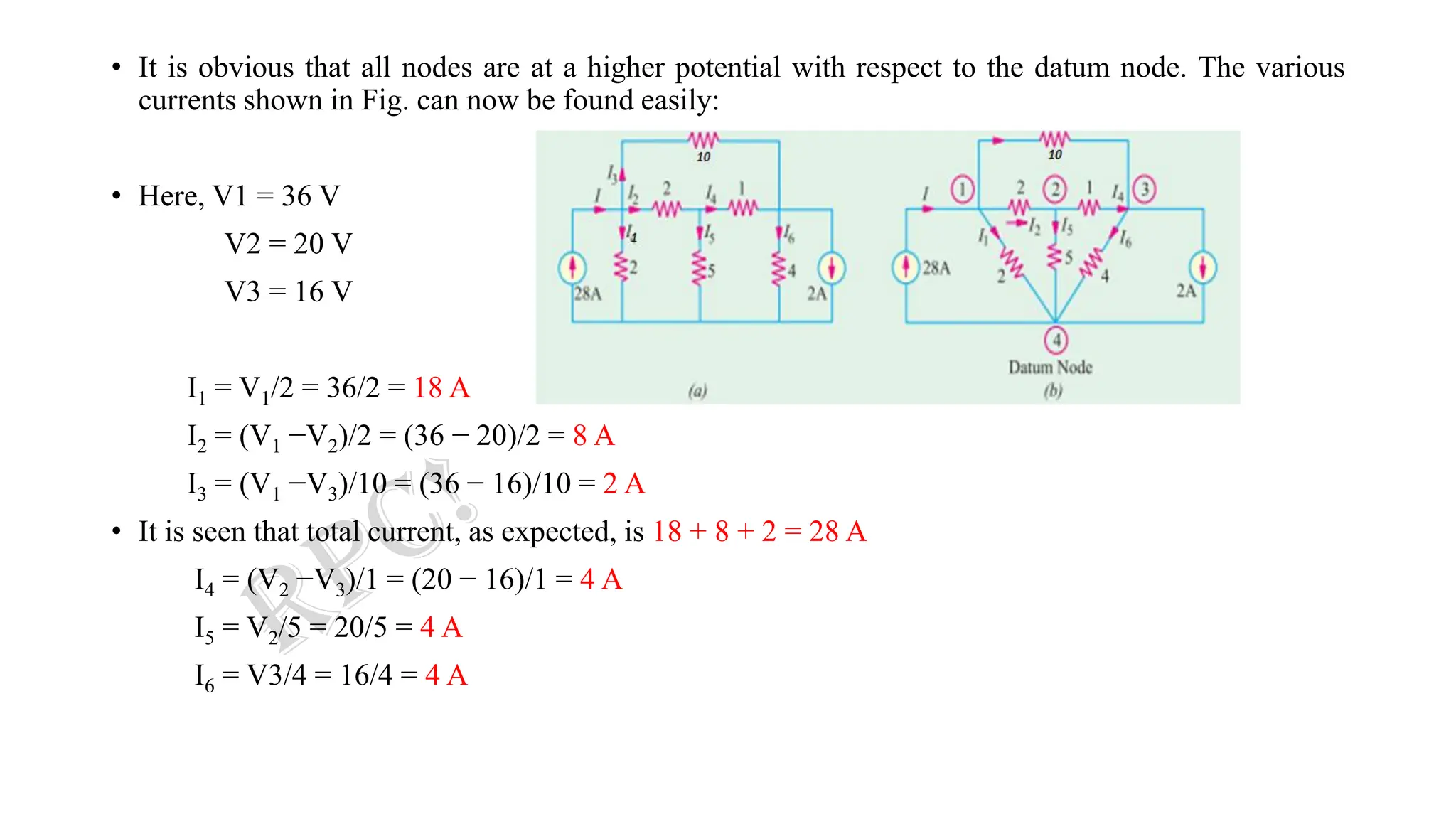
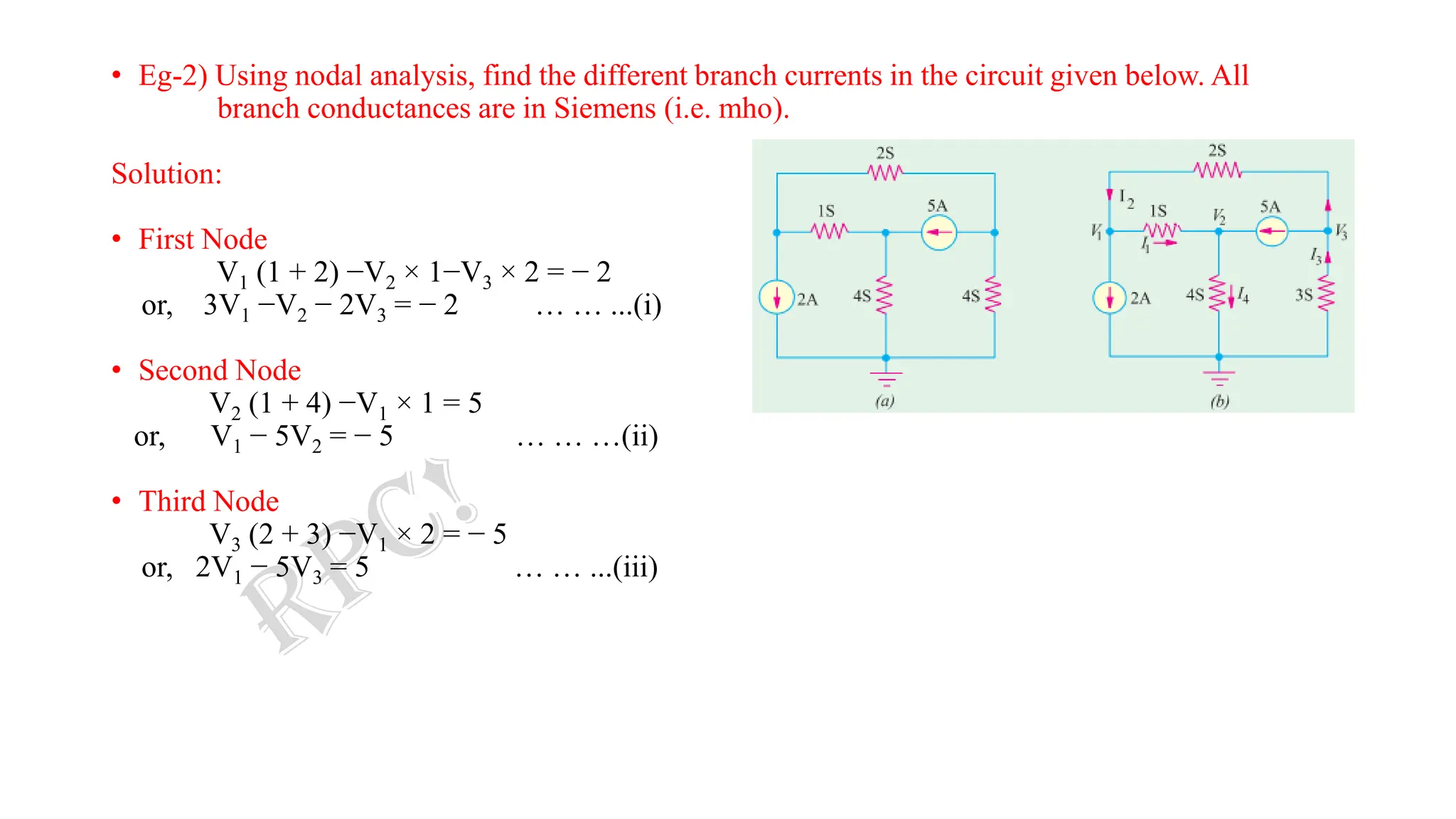
23. • Solving for the different voltages, we have:
• So,
I1 = (V1 −V2) × 1 = (− 1.5 − 0.7) × 1 = −2.2 A
I2 = (V3 −V1) × 2 = [− 1.6 − (− 1.5)] × 2 = −0.2 A
I4 = V2 × 4 = 4 × (7/10) = 2.8 A
I3 = 2 + 2.8 = 4.8 A
• As seen, I1 and I2 flow in directions opposite to those originally assumed.

24. • Eg-3) Use Nodal analysis to determine the value of current i in the given network.
Solution:
Here, i = V1/8
• For node 1:
V1(
1
8
+
1
4
) -
𝑉2
4
= 6 – 3i
or,
3
8
V1 –
𝑉2
4
+ 3
𝑉1
8
= 6 ( putting i = V1/8 )
or,
3
4
V1 –
𝑉2
4
= 6
or, 3V1 – V2 = 24 … … … (i)
• For node 2:
V2(
1
4
+
1
6
) -
𝑉1
4
= 3i
or, 3V1 = 2V2 … … … (ii)
• From eq. (i) and (ii):
V1 = 16 V
So, i = 16/8 = 2 A

25. Alternately:
• We will apply KCL to the two nodes 1 and 2. Equating the incoming currents at node 1 to the
outgoing currents, we have: