ELBO型VAEのダメなところ

1. ELBO型VAEのダメなところ
機械学習ゼミ
@UMU____
参考にした論文：Zhao, Shengjia, Jiaming Song, and Stefano Ermon. "Infovae:
Information maximizing variational autoencoders." arXiv preprint
arXiv:1706.02262 (2017).

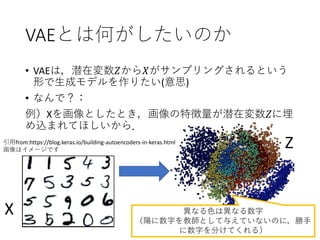
2. [pre]VAEとは何がしたいのか
• データ𝐷 = (𝑋 𝑖
, 𝑖 = 1, … , 𝑁)があります．
• 𝐷から生成モデル(generative model)を作りたい．
→生成モデルとは： 𝑋の母集団の確率分布𝑝 𝑅 𝑋 のこと．
または，𝑝 𝑅 𝑋 からサンプリングできる装置のこと．
• （有限の）𝐷からどうやって作るか→尤度最大化！
• 尤度最大化とは：
𝜃でパラメトライズされた確率分布 𝑝 𝜃(𝑋)を
𝐷を用いて𝑝 𝑅 𝑋 に近づけるためには， 𝜃を
𝜃 = argmax
𝜃
ෑ
𝑖
𝑝 𝜃(𝑋 𝑖)
とすればよいという考え方のこと（を尤度最大化という）．
データ𝐷がサンプリング
される確率を高くする
という意味

3. VAEとは何がしたいのか
• VAEは，潜在変数𝑍から𝑋がサンプリングされるという
形で生成モデルを作りたい(意思)
• なんで？：
例）Xを画像としたとき，画像の特徴量が潜在変数𝑍に埋
め込まれてほしいから．
X
Z
異なる色は異なる数字
（陽に数字を教師として与えていないのに，勝手
に数字を分けてくれる）
引用from:https://blog.keras.io/building-autoencoders-in-keras.html
画像はイメージです

4. VAEを作ろう
• 潜在変数の確率𝑝 𝑍 と，その分布からサンプリングさ
れた𝑍から𝑋がサンプリングされる条件付確率𝑝(𝑋|𝑍)を
作ることで，潜在変数を元にしたサンプリングを行う．
• VAEでは，𝑝 𝑍 は固定の分布， 𝑝 𝜃(𝑋|𝑍)を学習する．
𝜃は学習されるべきパラメータ．
• 最尤推定をしよう：(対数尤度の勾配を求められればよい）
∇ 𝜃 log 𝑝 𝑋 𝑖 = ∇ 𝜃 log න 𝑝 𝜃 𝑋 𝑖|𝑍 𝑝 𝑍 𝑑𝑍
勾配を求めなければいけない項に解析的に求められな
い積分が含まれてしまっている．．．（ダメじゃん）

5. VAEの秘策：ＥＬＢＯ
• log 𝑝(𝑋) は次のように分解できる：
log 𝑝 𝑋 =
log 𝑝 𝜃(𝑋|𝑍) 𝑞 𝜙(𝑍|𝑋) − 𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝑍 + 𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝜃 𝑍|𝑋
• ここで，𝑞 𝜙(𝑍|𝑋)はVAEの秘策のために導入された全く別の確率分布．
• もし， 𝑞 𝜙 𝑍 𝑋 = 𝑝 𝜃 𝑍|𝑋 になったとき， 𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝜃 𝑍|𝑋 =0
• もし，𝑞 𝜙 𝑍 𝑋 = 𝑝 𝜃 𝑍|𝑋 でないとき，常に𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝜃 𝑍|𝑋 > 0
• したがって，常に
log 𝑝 𝜃(𝑋|𝑍) 𝑞 𝜙(𝑍|𝑋) − 𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝑍 ≤ log 𝑝 𝑋
(左項がlog 𝑝 𝑋 の下界になっている！）
• 左側の項を最大化すれば， log 𝑝 𝑋 も最大化されるのでは．．．？
• 𝐿ELBO = log 𝑝 𝜃(𝑋|𝑍) 𝑞 𝜙(𝑍|𝑋) − 𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝑍
を最大化するのが，ELBO型VAE.(ELBO:Evidence Lower Bound)

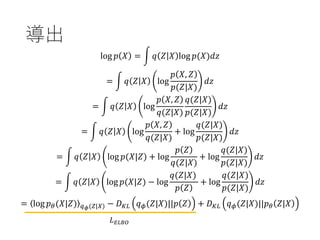
6. 導出
log 𝑝 𝑋 = න 𝑞 𝑍 𝑋 log 𝑝(𝑋)𝑑𝑧
= න 𝑞 𝑍 𝑋 log
𝑝 𝑋, 𝑍
𝑝(𝑍|𝑋)
𝑑𝑧
= න 𝑞 𝑍 𝑋 log
𝑝 𝑋, 𝑍
𝑞(𝑍|𝑋)
𝑞(𝑍|𝑋)
𝑝(𝑍|𝑋)
𝑑𝑧
= න 𝑞 𝑍 𝑋 log
𝑝 𝑋, 𝑍
𝑞(𝑍|𝑋)
+ log
𝑞(𝑍|𝑋)
𝑝(𝑍|𝑋)
𝑑𝑧
= න 𝑞 𝑍 𝑋 log 𝑝(𝑋|𝑍) + log
𝑝 𝑍
𝑞(𝑍|𝑋)
+ log
𝑞(𝑍|𝑋)
𝑝(𝑍|𝑋)
𝑑𝑧
= න 𝑞 𝑍 𝑋 log 𝑝(𝑋|𝑍) − log
𝑞(𝑍|𝑋)
𝑝 𝑍
+ log
𝑞(𝑍|𝑋)
𝑝(𝑍|𝑋)
𝑑𝑧
= log 𝑝 𝜃(𝑋|𝑍) 𝑞 𝜙(𝑍|𝑋) − 𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝑍 + 𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝜃 𝑍|𝑋
𝐿 𝐸𝐿𝐵𝑂

7. ＥＬＢＯ型VAEの実装法
• 𝐿ELBO = log 𝑝 𝜃(𝑋|𝑍) 𝑞 𝜙(𝑍|𝑋) − 𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝑍
を最大化
• 左項：𝑋 𝑖があって，分布qによって𝑍 𝑖に変換したものを，
分布pで𝑋′𝑖
に変換される確率（を高める）
→復元誤差についての項(復元誤差を小さく）
(左項のみ：AUTOENCODER)
• 右項：どんな𝑋 𝑖
から分布qによって得られる𝑍 𝑖
の分布も， 𝑝 𝑍 に近づかなければならない
→隠れ変数Zの分布を保証するための項
X Z X’
近づける 固定の分布に
積分が入らないので，
勾配法で解けます．
やったね．

8. ＥＬＢＯ型VAEについて
• MNIST(数字のデータセット)ではかろうじてう
まくいく
• 他のデータセットだとうまくいかない例が多々
報告されている．
→なんでうまくいかないんでしょう？？
今回の本題(残り3㌻)
本題より導入の方が長い

9. ＥＬＢＯ型VAEについて
ELBO型VAEの問題点として，論文[1]は
1. Z-X間の相互情報量が失われる問題
2. q(Z|X)が爆発する問題
の2つを挙げている．
これらの問題について簡単に述べる
[1]Zhao, Shengjia, Jiaming Song, and Stefano Ermon. "Infovae: Information maximizing variational
autoencoders." arXiv preprint arXiv:1706.02262 (2017).

10. Z-X間の相互情報量が失われる
問題
• 𝐿ELBOは次の形に書き換えられる．
• 𝐿ELBO = −⟨𝐷 𝐾𝐿 𝑞 𝜙 𝑍 𝑋 𝑝 𝜃 𝑍 𝑋
𝑝 𝑅 𝑋
− 𝐷 𝐾𝐿 (𝑝 𝑅 (𝑋)||𝑝 𝜃 (𝑋))
ここで，𝑝 𝜃(𝑋)が十分に複雑な表現力を持てた場合，𝑝 𝑅(𝑋)を十
分近似できるため，右項はゼロになる．
そのとき，ELBOは
⟨𝐷 𝐾𝐿 𝑞 𝜙 𝑍 𝑋 𝑝 𝜃 𝑍 𝑋
𝑝 𝑅 𝑋
= 0
のとき最大となる．
• しかしながら， ⟨𝐷 𝐾𝐿 𝑞 𝜙 𝑍 𝑋 𝑝 𝜃 𝑍 𝑋
𝑝 𝑅 𝑋
は， 𝑍と𝑋の相
互情報量がゼロ，すなわち𝑍を知ることで𝑋の情報が得られな
い，というときにゼロとなってしまう．
→潜在変数Zとはなんだったのか．．．
大問題

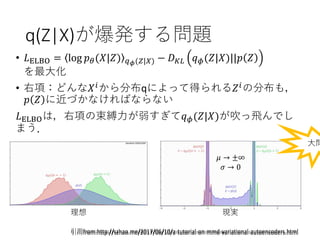
11. q(Z|X)が爆発する問題
• 𝐿ELBO = log 𝑝 𝜃(𝑋|𝑍) 𝑞 𝜙(𝑍|𝑋) − 𝐷 𝐾𝐿 𝑞 𝜙(𝑍|𝑋)||𝑝 𝑍
を最大化
• 右項：どんな𝑋 𝑖
から分布qによって得られる𝑍 𝑖
の分布も，
𝑝 𝑍 に近づかなければならない
𝐿ELBOは，右項の束縛力が弱すぎて𝑞 𝜙(𝑍|𝑋)が吹っ飛んでし
まう．
理想 現実
引用from:http://szhao.me/2017/06/10/a-tutorial-on-mmd-variational-autoencoders.html
大問
𝜇 → ±∞
𝜎 → 0
引用from:http://szhao.me/2017/06/10/a-tutorial-on-mmd-variational-autoencoders.html

12. ではこれら問題を解決するには
• これらの問題に関して、InfoVAE [1]では真に驚
くべき解決法を提案したが、45分でそれを発表
するには短すぎる．
→ [1]の論文を参照のこと(丸投げ)
[1]Zhao, Shengjia, Jiaming Song, and Stefano Ermon. "Infovae: Information maximizing
variational autoencoders." arXiv preprint arXiv:1706.02262 (2017).