This document provides an overview of POMDP (Partially Observable Markov Decision Process) and its applications. It first defines the key concepts of POMDP such as states, actions, observations, and belief states. It then uses the classic Tiger problem as an example to illustrate these concepts. The document discusses different approaches to solve POMDP problems, including model-based methods that learn the environment model from data and model-free reinforcement learning methods. Finally, it provides examples of applying POMDP to games like ViZDoom and robot navigation problems.

1. POMDP下での強化学習の
基礎と応⽤
尾崎安範

2. 尾崎安範 (@alfredplpl)
• 例によって⾃⼰紹介
サイバーエージェント 研究員 兼
⼤阪⼤学 招聘研究員 兼
⼤阪⼤学 ⽯⿊研究室 社会⼈博⼠２年⽣
← NTT研（開発寄り） 研究員
← 東⼤ 情報理⼯
最近やっていること
ロボットによる接客を強化学習する研究開発
POMDPなロボット接客を
強化学習したい︕

3. 今⽇の⽬標
• POMDPの問題設定と解法のアプローチを学ぶこととする
解法を厳密に説明すると１時間では終わらなくなるため、
問題設定とその問題設定があると認識してもらえることが⽬標とする
• また、POMDPの実問題を紹介し、
「こんな雰囲気で解くんだなぁ」と感じてもらうこととする
完全に理解するのはとてもではないが時間が⾜りない
• なお、私も理解が及んでないところもあるので、適宜参加者
の⽅で詳しい⼈がフォローしてもらえると助かります。

4. 今⽇のあらすじ
• POMDPの基礎
定式化
⻁問題
環境が既知である場合の解き⽅
環境が未知である場合の解き⽅
モデルフリーの解き⽅
モデルベースの解き⽅
• POMDPの応⽤
ゲーム
ロボット

5. 【おさらい】MDPとは
• マルコフ決定過程 (Markov Decision Process; MDP) とは現在の
⾏動と状態を必ず知ることができる状態遷移が確率的に起こ
る動的なモデルである。
• グラフィカルモデルで表現すると下の通り
[1]より引⽤

6. POMDPとは
• 部分観測マルコフ決定過程 (Partially Observable Markov
Decision Process; POMDP) は、⼀部しか観測できない状況であ
るモデルである。状態は直接わからない（潜在変数）。
MDPを⼀般化したモデルにあたる
• グラフィカルモデルで表現すると下の通り
[1]より引⽤

7. POMDPのイメージ
• ⼈⼿によるお掃除を考えてみよう
⼈は視野内のゴミを観測することができる。
しかし、視野外のゴミは観測することができない
• どうやってすべてのゴミを取り除けばよいのだろうか
⼈から⾒えるゴミ
⼈から⾒えないゴミ
⾒えている範囲

8. POMDPの定式化
• POMDPは離散時間の確率過程𝑃であると仮定すると、次のと
おりに定義される
𝑃 ≜ 𝒮, 𝒜, 𝑠!!
, 𝑝", 𝑟, 𝒪, 𝑝#
𝒮: 状態集合
𝒜: ⾏動集合
𝑠!!
: 初期状態の確率
𝑝": 状態遷移確率
𝑟: 報酬関数
𝒪: 観測集合
𝑝#: 観測遷移確率

9. 各種モデルの関係性
• 他のグラフィカルモデルとの位置づけを整理するとスッキリ
⾏動なし ⾏動あり
状態観測が完全 マルコフ連鎖 (MC) MDP
状態観測が⼀部 隠れマルコフモデル (HMM) POMDP
決定論 確率論
状態観測が完全 有限オートマトン マルコフ連鎖 (MC)
[15]より引⽤

10. 信念MDP
• POMDPをそのまま解くのではなくMDPの枠組みで解いてい
きたい。そこで、信念状態という考え⽅を導⼊する
• 信念状態𝑏$ 𝑠 はエージェントが潜在変数である状態が、ど
の状態にあるかというのを確率的に保持するための関数であ
る
• 信念状態𝑏$ 𝑠 を使うと、 𝑏$ 𝑠 と観測𝑜$%&で信念状態を更新
するような再帰式𝑏$%& 𝑠′ を作ることができる
したがって、履歴に直接よらなくなるため、マルコフ性は維持される
𝑏$ 𝑠 ≜ 𝑃𝑟 𝑆$ = 𝑠|𝐻$ = ℎ
履歴 ℎ (history) の定義:
ℎ ≜ 𝑎!, 𝑟!, 𝑜!, … , 𝑎"#$, 𝑟"#$, 𝑜"#$

11. POMDPの代表例: ⻁問題
• 具体的な代表例である⻁問題でPOMDPの理解を深めてみる
• ⻁問題とはドアが２つ左右にあり、どちらかには⻁がいて、
どちらかには宝があるという不確実な状態を想定する
⻁がいる⽅を開けてしまうと負の報酬
宝がある⽅を開けると正の報酬
ドアから⾳を聞くとちょっと負の報酬
信念状態
状態

12. ⻁問題の各変数
• ⻁問題（既知の環境）P = 𝒮, 𝒜, 𝑠!!
, 𝑝", 𝑟, 𝒪, 𝑝# は次の通り。
𝒮: {tiger-left, tiger-right}
𝒜: {open-left, open-right, listen}
𝑠!!
: 𝑠!!
𝑠 = tiger − left = 0.5, 𝑠!!
𝑠 = tiger − right = 0.5
𝑝": （次ページのとおり）
𝑟: （次ページのとおり）
𝒪: {left-sound, right-sound}
𝑝#: （次ページのとおり）

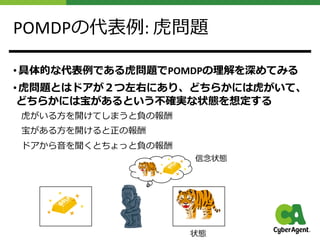
13. ⻁問題を状態遷移図にすると
• 各変数から状態遷移図を作ると以下の通り
• また観測確率関数は表の通り
[1]より引⽤

14. ⻁問題における信念状態と履歴
• ここではひたすらlistenすることを考える。その時の観測か
ら信念状態𝑏$ 𝑠 は再帰的に更新されていく
[1]より引⽤

15. 環境が既知である場合の解き⽅
• 実問題を解く上では環境は未知であることが多いので、
この場合は本発表では概要だけ説明する
• 環境が既知である場合、MDPと同様にプランニングにより解
くことができる。
• POMDPの厳密な解き⽅として、モナハンの価値反復法があ
る。しかし、組合せ爆発を起こす⼿法なので、実⽤的には使
われない。このため、点近似の価値反復法 (PBVI) がある。
モナハンの価値反復法を⼀回だけ反復した時の価値関数。
縦が信念状態に対する価値、
横が⻁が左にいるという信念状態
線の⾊が価値を最⼤にする⽅策
([1]より引⽤)

16. 環境が未知である場合の解き⽅
• モデルベースの場合とモデルフリーの場合の２つのパターン
に分かれる
さらにモデルベースではデータからプランニングするものと
シミュレータからプランニングするものに分かれる
モデルベースでの強化学習
（[1]より引⽤）
モデルフリーでの強化学習
（[1]より引⽤）

17. モデルベースの解き⽅
• データだけがある場合
⾏動を抜けばHMMであることからバウムウェルチアルゴリズムで遷移
確率を推定することができる。またノンパラベイズを使えば状態数すら
推定できる
• シミュレータがある場合
部分観測モンテカルロプランニング (POMCP) という解法がある
基本的にはモンテカルロ⽊探索の拡張版

18. モデルフリーの解き⽅
• モデルフリーでの解き⽅として、直近数ステップの観測を保
存するメモリなしのアプローチと、観測を全く保存せず⽅策
内部で記憶するメモリありのアプローチがある
• メモリなしの場合
SARSAなどを⽤いる
• メモリありの場合
ニューラルネットワークの⼀種LSTMを使い、
履歴を内部状態として記憶するアプローチを使う

19. POMDPの応⽤
• POMDPは実世界の様々な問題を表現することに適している
⼀⼈称シューティングゲーム
⾃動⾞の⾃動運転
対話システムの制御
その他は参考⽂献[3]を参照のこと
• ここではいくつかの具体例をあげて説明する

20. ゲームの例
• 例えば、⼀⼈称シューティングゲーム（FPS）の場合、環境
はゲーム空間になるが、プレイヤーは⾃分から⾒える範囲し
か観測できないことを前提としている
最たる例がViZDoom
ViZDoomの画⾯とメタデータ（[4]より引⽤）

21. ViZDoomの定式化例
• ViZDoom P = 𝒮, 𝒜, 𝑠!!
, 𝑝", 𝑟, 𝒪, 𝑝# を定式化した結果はたくさ
んあるし、シナリオによるが、たとえば以下の通りとなる。
𝒮: 位置、健康状態、弾数
𝒜: {左に動く, 右に動く, 撃つ}
𝑠!!
: 中央に固定
𝑝": （未知）
𝑟: 敵を倒した、時間切れ
𝒪: マップ内で⾒れる⼀⼈称の画像すべて
𝑝#:（未知） [5]より引⽤

22. ViZDoomのベースライン解法
• MDPとして考えて、関数近似で解く[5]
畳み込みニューラルネットワークを使って、⽅策をDQNで解く
状態は全く記憶できていない
[5]より引⽤

23. ViZDoomの改善された解法
• LSTMによるメモリありのアプローチを採⽤する[6]
[6]より引⽤

24. ロボットの例
• ロボットではナビゲーションなどの問題がPOMDPとなる。
• 例えば、市街地における⾃動⾞の⾃動運転の場合、環境は実
世界の市街地を対象とするが、実世界そのものを完全に把握
することはできない。そこで、センサからの情報などしか観
測できないことを前提としている
[7]より引⽤

25. ⾃動運転の定式化例
• ⾃動運転 P = 𝒮, 𝒜, 𝑠!!
, 𝑝", 𝑟, 𝒪, 𝑝# を定式化した結果は、
たとえば以下の通りとなる。
𝒮: 三次元位置など
𝒜: アクセル、ブレーキ、ステアリングなど
𝑠!!
: 駐⾞場が⾼い分布（ほぼ未知）
𝑝": （未知）
𝑟: ⽬的地に到達したかどうか
𝒪: 世界から得られる画像すべて（ほぼ未知）
𝑝#:（未知）

26. ⾃動運転へのアプローチ
• アプローチはいくつか提案されている[7]
⼈が運転した結果を模倣
シミュレータで獲得した⽅策を実世界に転移
• また、制御の抽象度によっても分類されている[8]
センサの値から⾏動する
センサの値と経路のプランニング結果から⾏動する
などなど
• ただし、POMDPで定式化して実世界に適⽤した例は
とても少ない

27. • 実世界で⼈間が運転した結果を元にニューラルネットワーク
を⾏動を模倣させ、実世界にも試してみた[9]
POMDPであることはあまり気にしていない気がする
⾃動運転の解き⽅の代表例
[9]より引⽤

28. ⾃動運転の解き⽅の例
• 駐⾞場で移動するタスクにおいて、シミュレータ環境で深層
学習させた結果を実世界に適⽤した[10]
というMDPとはいうけど、
POMDPに近い気がする
[10]より引⽤

29. まとめ
• 部分観測マルコフ決定過程 (Partially Observable Markov
Decision Process; POMDP) は、⼀部しか観測できない状況であ
るモデルである。状態は直接わからない。
環境が既知であるとき、モナハンの価値反復法で解ける
環境が未知であるとき、部分観測モンテカルロプランニングなどで解く
近年では深層強化学習を使って近似的に解くことが多い
• POMDPの解法を本発表よりも詳しく学びたい⼈は参考⽂献
[1,2,13,14]を読んでください
• また、POMDPの問題を実際に解いてみたいという⼈は参考
⽂献[14]にソルバーがあるので使ってみてください

30. おまけ１︓LSTMの有効性
• MDPなゲームをたまに画⾯を隠すことでPOMDPにした場合、
DQNにLSTMをいれるとスコアが改善した[11]
[11]より引⽤

31. 参考⽂献
[1] 森村哲郎, “強化学習 (機械学習プロフェッショナルシリーズ),” 2019
[2] セバスチャン・スランら, “確率ロボティクス”, 2007
[3] Cassandra et al., “A Survey of POMDP Applications,”
[4] Wydmuch et al., “ViZDoom Competitions: Playing Doom from Pixels,” 2018,
https://github.com/mwydmuch/ViZDoom
[5] Kempka, et al., “ViZDoom: A Doom-based AI Research Platform for Visual
Reinforcement Learning,” 2016
[6] Lample et al., “Playing FPS Games with Deep Reinforcement Learning”, 2016

32. 参考⽂献
[7] Kiran et al., “Deep Reinforcement Learning for Autonomous Driving: A Survey” 2020
[8] Zhu., “A Survey of Deep RL and IL for Autonomous Driving Policy Learning,” 2021
[9] Bojarski et al., “End to End Learning for Self-Driving Cars,” 2016
[10] Folkers et al., “Controlling an Autonomous Vehicle with Deep Reinforcement
Learning,” 2019
[11] Hausknecht et al., “Deep Recurrent Q-Learning for Partially Observable MDPs” 2015
[12] “POMDPs for Dummies”,
https://cs.brown.edu/research/ai/pomdp/tutorial/index.html
[13] 牧野ら, “これからの強化学習”, 2016
[14] Anthony R. Cassandra, “The POMDP Page”, https://www.pomdp.org/
[15] 渡辺有祐、”グラフィカルモデル” 2016