1. GoDec: Randomized Low-rank &
Sparse Matrix Decomposition in
Noisy Case
#41
Tianyi Zhou, Dacheng Tao @niam
江原 遥
1

2. この論文を読もうと思った動機
• 2009 乱択化SVD (Halko+)
– Gaussian行列をかけて列を圧縮．SVDを高速近似．
– ノルムをバウンドして近似の良さを証明
• 2010/9 REDSVD (Okanohara+)
– 実用的には行と列の両方を圧縮してよい
• 2011/3 全部分文字列のクラスタリングとそ
の応用 (岡野原, NLP2011)
– REDSVDを全部分文字列のクラスタリングに応用
2

3. この論文を読もうと思った動機
• 2009 乱択化SVD (Halko+)
– Gaussian行列をかけて列を圧縮．SVDを高速近似．
GoDec論文では
– ノルムをバウンドして近似の良さを証明andomProjection
BilateralR
• 2010/9 REDSVD (Okanohara+) と呼んでいる
– 実用的には行と列の両方を圧縮してよい
• 2011/3 全部分文字列のクラスタリングとそ
の応用 (岡野原, NLP2011)
– REDSVDを全部分文字列のクラスタリングに応用
3

4. Abstractには
The algorithm can be significantly accelerated by
bilateral random projections (BRP).
Theoretically, we analyze the influence of L, S and
G to the asymptotic/convergence speeds in order to
discover the robustness of GoDec.
Fast GoDec
と書いてあるので，いかにもBRPを適用した場合の証
明が書いてありそうに見えるが… Nai:ve GoDec
どうやら証明されているのは近似なしのGoDeC
4

5. 特異値分解
(Singular Value Decomposition)
X: m x nデータ行列
r:自然数 が与えられたとき
minL ||X-L||F
s.t. rank(L)=r
をみたすLは，
X  U V Tの大きい方からr個の特異値(>0)を用いて
r
L   iui v iと表せる．
i 1
時間計算量 mnr （たぶん）
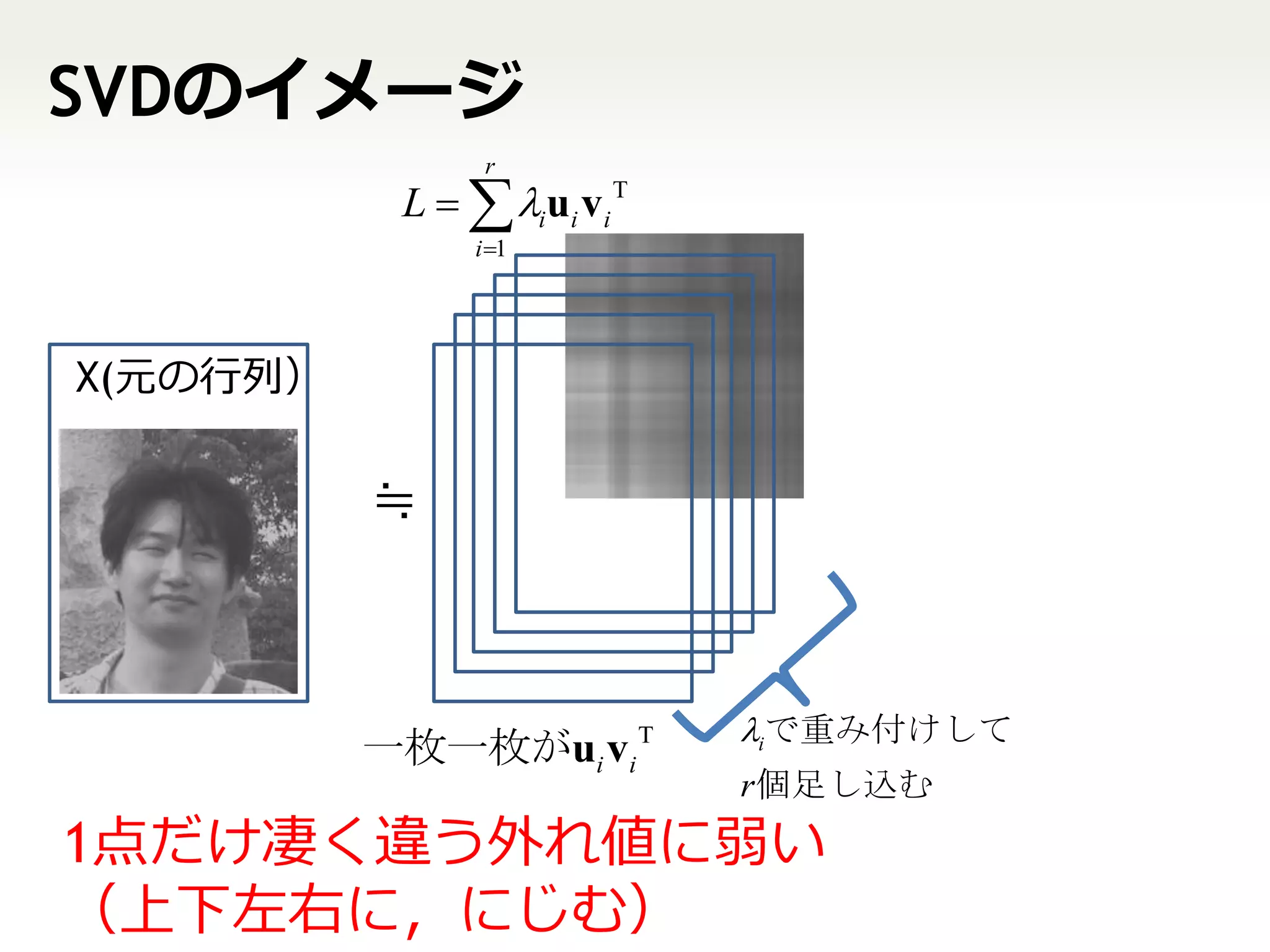
5

6. SVDのイメージ
r
L   iui vi T
i 1
X(元の行列）
≒
iで重み付けして
一枚一枚がui vi T
r 個足し込む
1点だけ凄く違う外れ値に弱い
（上下左右に，にじむ）

7. 実際，SVDはどんな感じににじむか
180x200行列 (rank180) rank10で低ランク近似
7

8. 解決策：外れ値に弱いなら
外れ値を抜けばいいじゃない r
外れ値の
L   u v i i i
T
個数=
i 1 card(S)
X(元の行列）
S
≒ ＋
iで重み付けして
一枚一枚がui v i T
r個足し込む

9. Nai:ve GoDec
今までの話を数式で書くと解きたい問題は：
LとSを同時に最適化するのは難しい．
次の様にLとSを交互に計算できれば簡単．
Robust PCAの論文から
は 取ってきた（汗
こう解けばOK：
は
こう解けばOK：
9

10. Nai:ve GoDec
今までの話を数式で書くと解きたい問題は：
LとSを同時に最適化するのは難しい．
次の様にLとSを交互に計算できれば簡単．
は
こう解けばOK：
は
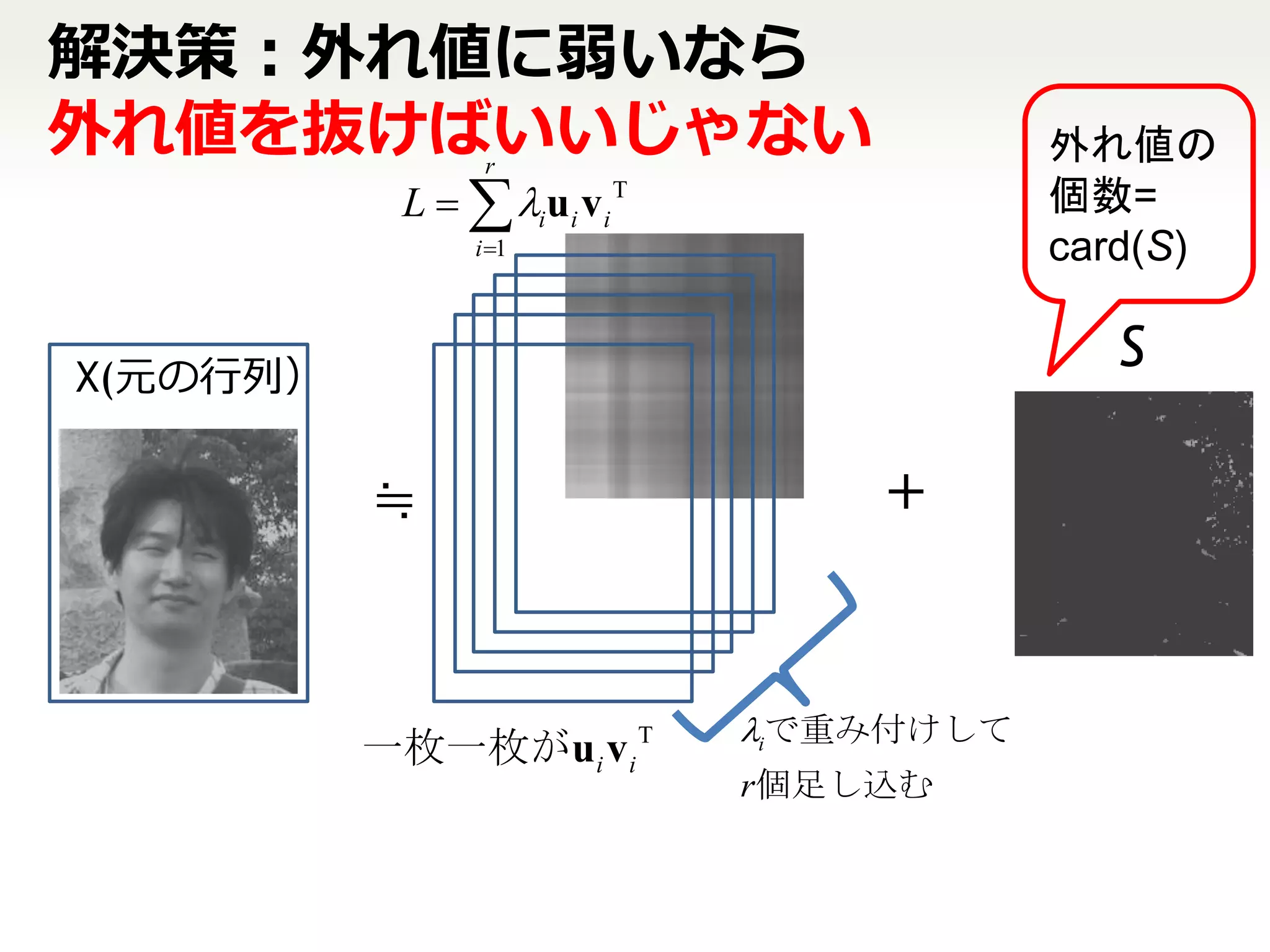
こう解けばOK：
10

11. Nai:ve GoDec
今までの話を数式で書くと解きたい問題は：
Dense（黒っぽい）Lと
Sparse（白っぽい）Sを交互に
扱う点が碁に似てるからGoDec
LとSを同時に最適化するのは難しい．
次の様にLとSを交互に計算できれば簡単．
この論文の貢献：
• Theorem 1:
は
この交互計算がlocal minimum
こう解けばOK： に収束する
• Theorem 2, 3:
はノイズがなければ線形収束する
• Theorem 4:
こう解けばOK： ノイズがあってもノイズが酷く
なければ線形収束する 11

12. Nai:ve GoDecの問題点
今までの話を数式で書くと解きたい問題は：
遅い．毎iterationでsvdするとか
やりたくない．高速化したい．
→Fast GoDec
LとSを同時に最適化するのは難しい．
次の様にLとSを交互に計算できれば簡単．
は
こう解けばOK：
は
こう解けばOK：
12

13. Fast GoDec
BRP +
Power
Scheme
以後，
近似手法
を説明
Stの計算は同じ
13

14. 元々やりたいこと：
BRP
こうやれば厳密に解けるが遅い
…と書いてあるがr個ま
計算量： でなのでmnr
A1 :列を圧縮するランダム行列
A2 :行を圧縮するランダム行列 を用いて高速化
発表者が知る方法は３つ Y1  XA1 , Y2  X T A2
本論文
Y1r  U  V , Y2 r  U 2  2 rV2 , L  Y1r  A2 Y1r  Y2 r
†
(Fazel+, 1 1r 1
T T T
2008)
Y1  Q1 R1 , Y2  Q2 R2 , C  Q2T XQ1  USV T
REDSVD:
L Q2CQ1T  Q2USV T Q1T
14

15. 元々やりたいこと：
BRP
こうやれば厳密に解けるが遅い
…と書いてあるがr個ま
計算量： でなのでmin(mr2,nr2)?
A1 :列を圧縮するランダム行列
A2 :行を圧縮するランダム行列 を用いて高速化
発表者が知る方法は３つ Y1  XA1 , Y2  X T rAx rの逆行列を使う
2
本論文
r x rのSVD 2回+ r x rの逆行列を使う
(Fazel+, Y1r  U11rV1T , Y2 r  U 2  2 rV2T , L  Y1r  A2T Y1r  Y2 r
†
2008)
r x rのSVDを１回使う
REDSVD: Y1  Q1 R1 , Y2  Q2 R2 , C  Q2T XQ1  USV T
L Q2CQ1T  Q2USV T Q1T 15

16. 元々やりたいこと：
BRP
こうやれば厳密に解けるが遅い
…と書いてあるがr個ま
計算量： でなのでmin(mr2,nr2)?
A1 :列を圧縮するランダム行列
A2 :行を圧縮するランダム行列 を用いて高速化
発表者が知る方法は３つ Y1  XA1 , Y2  X T A2
本論文
(Fazel+, Y1, Y2のランクはrなので， Y1r= Y1, Y2r = Y2
だから実は２つは同じでSVDの計算はいらない．
2008)
Y1r  Y1  U  V , Y2 r  Y2  U 2  2 rV2 , L  Y1  A2 Y1  Y2
T T T 1
1 1r 1
条件付きだが||X-L||のBoundが
示されている (Woolfe+, 2008) 16

17. Power scheme
特異値の減衰が遅いと低ランク近似したときに誤差が
大きくなる．
解決策：Xの代わりに X   XX  Xを低ランク近似
T q
Xの特異値を大きい順にλiとすると， (XXT)qXの特異
値はλi2q+1になるので（特異ベクトルはXと同じ）早
く減衰．
しかし，元に戻すために(XXT)-q の計算をするのなら
無意味．→QR分解
17

18. QR分解
X: m x n
A1: n x r
A2: m x r
Y1=XA: m x r
A2TY1: r x r →QR分解を利用（累乗計算のため）
R1: p x r
Q1: m x p
18

19. 証明
Naïve GoDecの
local minimumへの
収束証明と1次収束証明
がなされている．
Fast GoDecは
証明なし（たぶん）
収束証明は簡単：
19

20. 1次収束証明
• Theorem 2, 3:ノイズがなければ線形収束する
• Theorem 4: ノイズがあってもノイズが酷く
なければ線形収束する
証明の概略: これの挙動を見る
Robust PCA （40ページ）の論文の証明技法と同様の方法を
使っているらしく，おそらく，これを読まないとちゃんと
理解出来ない． 20

21. 実装：Nai:ve GoDecなら簡単
https://github.com/niam/godec/blob/master/src/godec.cpp
void run(const emat_t& X, const int r, const int k, const val_t eps ){
int loop= 0; val_t norm_rate = 0.0;
val_t xnorm = X.norm();
L_t = X;
S_t; S_t.setZero(X.rows(), X.cols());
do{
Eigen::JacobiSVD<emat_t> svd(X-S_t, Eigen::ComputeThinU | Eigen::ComputeThinV);
auto sigmas = svd.singularValues();
for(int i=r; i< sigmas.size();++i)sigmas[i]=0; SVDする
L_t = svd.matrixU()*sigmas.asDiagonal()*svd.matrixV().transpose();
S_t.setZero(X.rows(), X.cols());
select_kbest(S_t, X-L_t, k, Abs());
外れ値を抜く
norm_rate = (X-L_t-S_t).norm()/xnorm;
cout << loop++ << ": " << norm_rate << "=" << (X-L_t-S_t).norm() << "/" << xnorm << endl;
}
}while(norm_rate > eps);
繰り返す
21

22. 実験 (Nai:ve GoDec)
元画像：
200x180
22

23. 使用メモリ量を合わせるため，rが違う
SVDと比較 GoDeCの方がSの非0の分メモリを使用
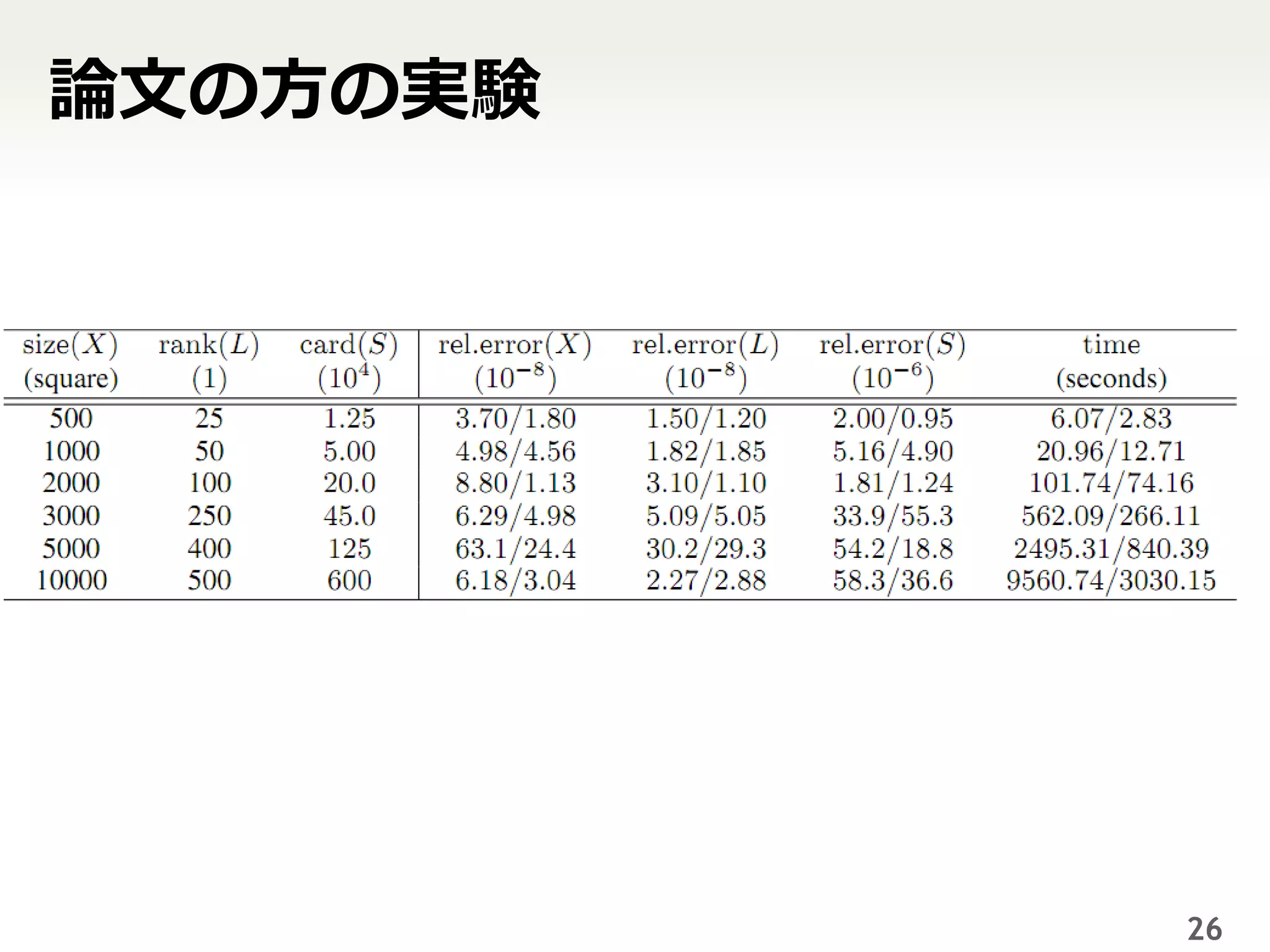
SVD r=10 Naive GoDec L+S r=8, k=762
23

24. 結果...
reading ||X-L||= 4830.8
FILE_NAME = writing L...
/home/ehara/mypic.png Succeeded in writing?: 1
width = 180 ||X-S||= 25578.7
height = 200 writing S...
bpp =3 Succeeded in writing?: 1
0: 0.140223=3611.84/25757.9 ||X-LpS||= 3333.06 SVDより
1: 0.133084=3427.97/25757.9 writing LpS... 誤差小さい
2: 0.131239=3380.44/25757.9 Succeeded in writing?: 1
（中略） ||X-svd||= 4089.61
20: 0.1294=3333.08/25757.9 writing svd...
21: 0.1294=3333.06/25757.9 Succeeded in writing?: 1
収束してる writing X...
Succeeded in writing?: 1
200 x 180行列
だから…→ 4.73 user 0.02 system 99% cpu 4.779 total
24

25. 論文の方の実験
25

26. 論文の方の実験
26

27. まとめ
• SVDでの低ランク近似は，外れ値に弱い
→外れ値を抜きながら低ランク近似する
低ランク：L, 外れ値：S, もとの行列X≒L+S
• Nai:ve GoDecがlocal minimumに線形収束すること
を証明している．ただし，毎イテレーションごとに
SVDを実行するので遅い．
• ランダム行列を使って，近似的に高速に計算できる．
ただし，こちらには証明がない（たぶん）
アイデアは良いが，細部が抜けている論文だと感じた．
（Algorithm 2を参照しながらAlgorithm 1までしかない
とか） 27

28. 参考文献
Fazel, M., Cand` es, E. J., Recht, B., and Parrilo, P. Compressed sensing and
robust recovery of low rank matrices. In 42nd Asilomar Conference on Signals,
Systems and Computers, 2008
Cand` es, E. J., Li, X., Ma, Y., and Wright, J. Robust principal component
analysis? Journal of the ACM (submitted), 2009.
Halko, N., Martinsson, P. G., and Tropp, J. A. Finding structure with randomness:
Stochastic algorithms for constructing approximate matrix decompositions. arXiv:
0909.4061, 2009.
Zhou, T. and Tao, D. Bilateral random projection based low-rank approximation.
Technical report, 2010.
28

29. ご清聴ありがとうございました
29