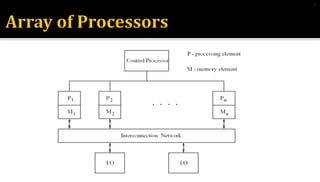
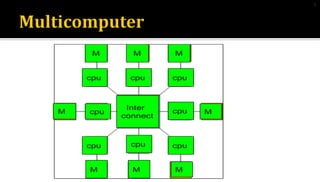
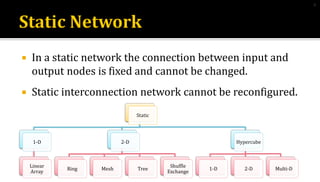
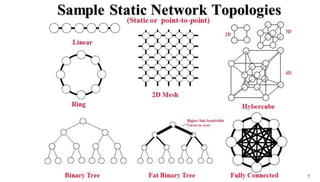
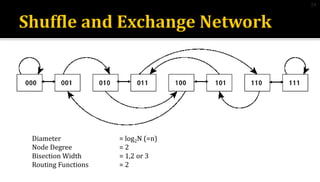
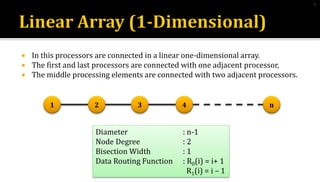
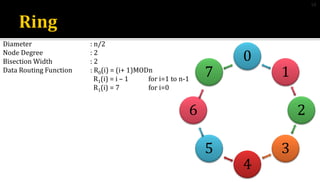
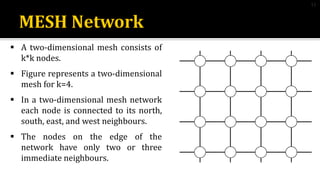
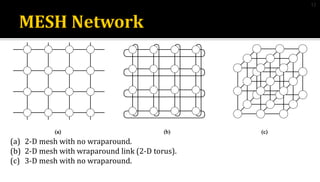
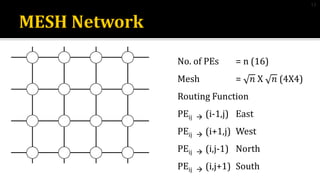
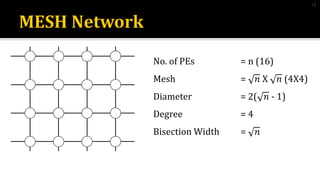
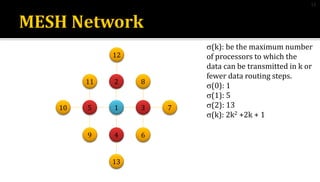
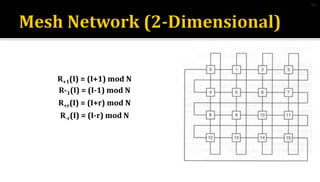
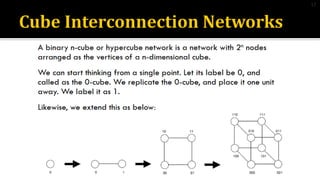
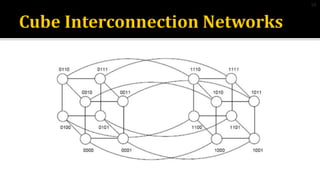
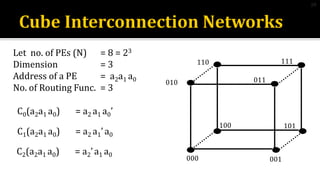
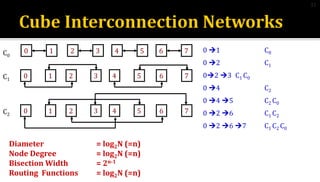
This document discusses different types of interconnection network topologies for parallel machines. It provides details on: 1) Linear array networks have nodes connected in a line, with diameter of n-1, node degree of 2, and bisection width of 1. 2) Mesh networks connect nodes in a grid, with diameter of 2(n-1), node degree of 4, and bisection width of n for an nXn mesh. 3) Hypercube networks have nodes connected by log2N routing functions, with diameter and node degree of log2N and bisection width of 2n-1 for a network with N nodes.

1. By Dr. Heman Pathak
1

2. 2

3. 3

4. An interconnection network in a parallel
machine transfers information from any source
node to any desired destination node.
The network is composed of links and switches,
which helps to send the information from the
source node to the destination node. A network is
specified by its topology & routing algorithm.
4

5. Topology: It indicates how the nodes in a network are organised.
Interconnection Network
Static
1-D 2-D Hypercube
Dynamic
Bus Based
Single Multiple
Switch
Based
Single
Stage
Multi Stage Crossbar
5

6.  In a static network the connection between input and
output nodes is fixed and cannot be changed.
 Static interconnection network cannot be reconfigured.
Static
1-D
Linear
Array
2-D
Ring Mesh Tree
Shuffle
Exchange
Hypercube
1-D 2-D Multi-D
6

7. 7

8. • It is the minimum distance between the farthest nodes in a network. The distance is measured
in terms of number of distinct hops between any two nodes.
Network Diameter:
• Number of edges connected with a node is called node degree.
Node Degree:
• Number of edges required to be cut to divide a network into two halves is called bisection
bandwidth.
Bisection Bandwidth:
• The data routing functions are the functions which when executed establishes the path between
the source and the destination.
Data Routing Functions:
8

9.  In this processors are connected in a linear one-dimensional array.
 The first and last processors are connected with one adjacent processor,
 The middle processing elements are connected with two adjacent processors.
1 2 3 4 n
Diameter : n-1
Node Degree : 2
Bisection Width : 1
Data Routing Function : R0(i) = i+ 1
R1(i) = i – 1
9

10. Diameter : n/2
Node Degree : 2
Bisection Width : 2
Data Routing Function : R0(i) = (i+ 1)MODn
R1(i) = i – 1 for i=1 to n-1
R1(i) = 7 for i=0
0
1
2
3
4
5
6
7
10

11.  A two-dimensional mesh consists of
k*k nodes.
 Figure represents a two-dimensional
mesh for k=4.
 In a two-dimensional mesh network
each node is connected to its north,
south, east, and west neighbours.
 The nodes on the edge of the
network have only two or three
immediate neighbours.
11

12. (a) 2-D mesh with no wraparound.
(b) 2-D mesh with wraparound link (2-D torus).
(c) 3-D mesh with no wraparound.
12

13. No. of PEs = n (16)
Mesh = 𝑛 X 𝑛 (4X4)
Routing Function
PEij  (i-1,j) East
PEij  (i+1,j) West
PEij  (i,j-1) North
PEij  (i,j+1) South
13

14. No. of PEs = n (16)
Mesh = 𝑛 X 𝑛 (4X4)
Diameter = 2( 𝑛 - 1)
Degree = 4
Bisection Width = 𝑛
14

15. (k): be the maximum number
of processors to which the
data can be transmitted in k or
fewer data routing steps.
(0): 1
(1): 5
(2): 13
(k): 2k2 +2k + 1
1
5 3
2
4
7
8
6
10
11
9
12
13
15

16. R+1(I) = (I+1) mod N
R-1(I) = (I-1) mod N
R+r(I) = (I+r) mod N
R-r(I) = (I-r) mod N
16

17. 17

18. 18

19. No. of PEs are = N = 2n
Dimension = n = log2N
Address of a PE = n-bit Binary Address an-1 an-2…. a1 a0
There are n Routing Functions as -
C0(an-1 an-2…. a1 a0) = an-1 an-2…. a1 a0’
C1(an-1 an-2…. a1 a0) = an-1 an-2…. a1’ a0
Cn-1(an-1 …. ai… a0) = an-1’ an-2…. ai ….a0
Ci(an-1 …. ai… a0) = an-1 an-2…. ai’ ….a0
For i = 0,1,2,…..n-1
19

20. Let no. of PEs (N) = 8 = 23
Dimension = 3
Address of a PE = a2a1 a0
No. of Routing Func. = 3
000 001
010
100
C0(a2a1 a0) = a2 a1 a0’
C1(a2a1 a0) = a2 a1’a0
C2(a2a1 a0) = a2’a1 a0
101
011
110 111
20

21. 0 1 2 3 4 5 6 7
C0
0 1 2 3 4 5 6 7
C1
0 1 2 3 4 5 6 7
C2
0 1 C0
0 2 C1
02 3 C1 C0
0 4 C2
0 4 5 C2 C0
0 2 6 C1 C2
0 2 6 7 C1 C2 C0
Diameter = log2N (=n)
Node Degree = log2N (=n)
Bisection Width = 2n-1
Routing Functions = log2N (=n)
21

22. 0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
000 (0) = 000 (0)
001 (1) = 010 (2)
010 (2) = 100 (4)
011 (3) = 110 (6)
100 (4) = 001 (1)
101 (5) = 011 (3)
110 (6) = 101 (5)
111 (7) = 111 (7)
The Perfect Shuffle
0
1
2
3
4
5
6
7
000 (0) = 001 (1)
010 (2) = 011 (3)
100 (4) = 101 (5)
110 (6) = 111 (7)
Exchange
22

23. No. of PEs are N = 2n
Address of a PE an-1 an-2…. a1 a0
This network is based on two routing functions –
Shuffle : S(an-1 an-2…. a1 a0) = an-2…. a1 a0 an-1
Exchange : E(an-1 an-2…. a1 a0) = an-1an-2…. a1 a0 ‘
23

24. Diameter = log2N (=n)
Node Degree = 2
Bisection Width = 1,2 or 3
Routing Functions = 2
24