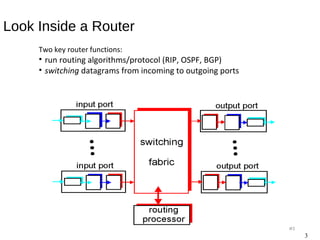
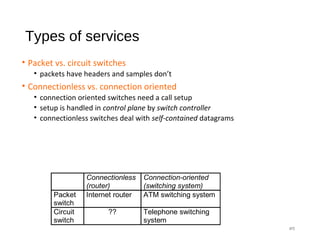
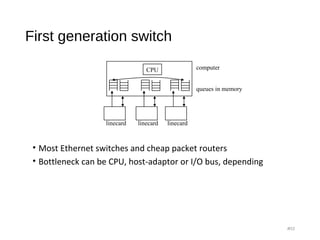
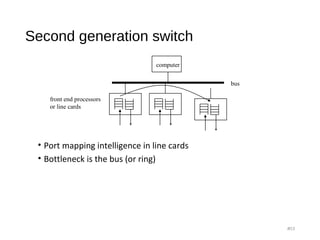
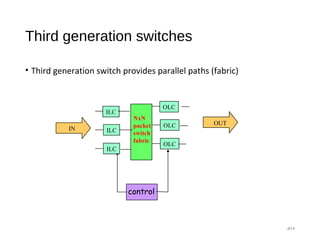
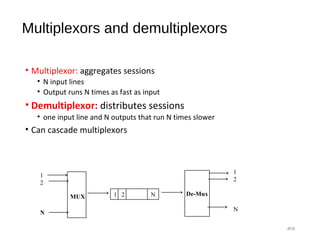
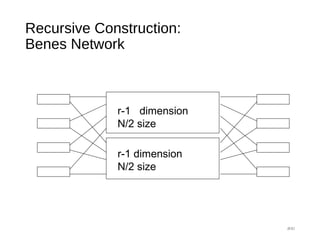
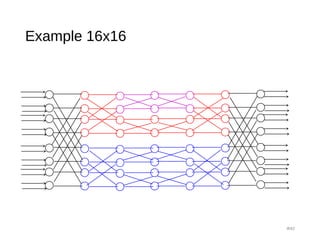
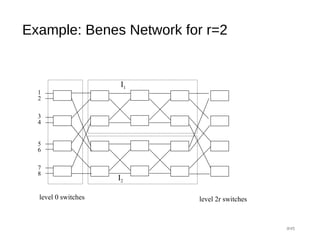
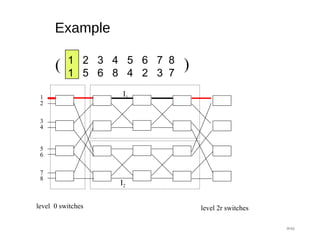
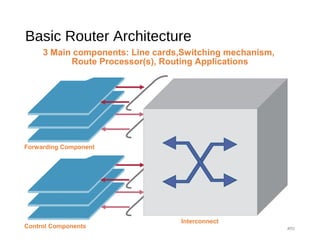
The document provides an overview of various switching mechanisms including telephone switches, routers, and packet switches, explaining their functionalities and types such as circuit- and connection-oriented switching. It discusses the importance of internal switching mechanisms, blocking issues in packet switching, and methods to handle such blockages along with the evolution and generations of packet switches. Additionally, the document delves into specific switching architectures like Clos networks, Benes networks, and their complexity, scalability, and non-blocking properties.

1. Switching Units

2. Types of switching elements
• Telephone switches
• switch samples
• Datagram routers
• switch datagrams
• ATM switches
• switch ATM cells
#2
INPUTS
OUTPUTS

3. #3
Look Inside a Router
Two key router functions:
• run routing algorithms/protocol (RIP, OSPF, BGP)
• switching datagrams from incoming to outgoing ports
3

4. Repeaters, bridges, routers, and
gateways
• Repeaters/Hubs: at physical level (L1)
• Bridges: at datalink level (L2)
• based on MAC addresses
• discover attached stations by listening
• Routers: at network level (L3)
• participate in routing protocols
• Application level gateways: at application level (L7)
• treat entire network as a single hop
• Gain functionality at the expense of forwarding speed
• for best performance, push functionality as low as possible
#4

5. Types of services
• Packet vs. circuit switches
• packets have headers and samples don’t
• Connectionless vs. connection oriented
• connection oriented switches need a call setup
• setup is handled in control plane by switch controller
• connectionless switches deal with self-contained datagrams
#5
Connectionless
(router)
Connection-oriented
(switching system)
Packet
switch
Internet router ATM switching system
Circuit
switch
?? Telephone switching
system

6. Other switching unit functions
• Participate in routing algorithms
• to build routing tables
• Next Lecture!
• Resolve contention for output trunks
• buffer scheduling
• Previous Lecture!
• Admission control
• to guarantee resources to certain streams
#6

7. Requirements
• Capacity of switch is the maximum rate at which it can move
information, assuming all data paths are simultaneously
active
• Primary goal: maximize capacity
• subject to cost and reliability constraints
• Circuit switch must reject call if can’t find a path for samples
from input to output
• goal: minimize call blocking
• Packet switch must reject a packet if it can’t find a buffer to
store it awaiting access to output trunk
• goal: minimize packet loss
• Subgoal: Don’t reorder packets
#7

8. Internal switching
• In a circuit switch, path of a sample is determined at time of
connection establishment
• No need for a sample header--position in frame is enough
• In a packet switch, packets carry a destination field
• Need to look up destination port on-the-fly
• Datagram
• lookup based on entire destination address
• Cell
• lookup based on VCI – used as an index to a table
• Other than that, switching units are very similar
#8

9. Blocking in packet switches
• Can have both internal and output blocking
• Internal
• no path to output
• Example: head of line blocking.
• Output
• output link busy
• If packet is blocked, must either buffer or drop it
#9

10. Dealing with blocking
• Overprovisioning
• internal links much faster than inputs
• Buffers
• at input or output
• Backpressure
• if switch fabric doesn’t have buffers, prevent packet from entering until path
is available
• Parallel switch fabrics
• increases effective switching capacity
#10

11. Three generations of packet switches
• Different trade-offs between cost and performance
• Represent evolution in switching capacity, rather than in technology
• With same technology, a later generation switch achieves greater capacity,
but at greater cost
• All three generations are represented in current products
#11

12. First generation switch
• Most Ethernet switches and cheap packet routers
• Bottleneck can be CPU, host-adaptor or I/O bus, depending
#12
computer
queues in memory
CPU
linecard linecard linecard

13. Second generation switch
• Port mapping intelligence in line cards
• Bottleneck is the bus (or ring)
#13
bus
computer
front end processors
or line cards

14. Third generation switches
• Third generation switch provides parallel paths (fabric)
#14
NxN
packet
switch
fabric
OLC
OLC
OLC
IN
ILC
ILC
ILC
OUT
control

15. Third generation (contd.)
• Features
• self-routing fabric
• output buffer is a point of contention
• unless we arbitrate access to fabric
• potential for unlimited scaling,
• as long as we can resolve contention for output buffer
#15

16. Switching - Fabric

17. Switching: abstract model
#17
Number of connections: from few (4 or 8) to huge (100K)

18. Multiplexors and demultiplexors
• Multiplexor: aggregates sessions
• N input lines
• Output runs N times as fast as input
• Demultiplexor: distributes sessions
• one input line and N outputs that run N times slower
• Can cascade multiplexors
#18
De-Mux
1
2
N
1
2
N
1 2 NMUX

19. Time division switching
• Key idea: when demultiplexing, position in frame determines output
link
• Time division switching interchanges sample position within a
frame:
• Time slot interchange (TSI)
#19
M
U
X
D
E
M
U
X
TSI

20. Time Slot Interchange (TSI) : example
#20
sessions: (1,3) (2,1) (3,4) (4,2)
4 3 2 1 3 1 4 2
1
2
3
4
Read and write to shared memory in different order
1
2
3
4
2
4
1
3

21. TSI
• Simple to build.
• Multicast: easy (why?)
• Limit is the time taken to read and write to memory
• For 120,000 telephone circuits
• Each circuit reads and writes memory once every 125 ms.
• Number of operations per second : 120,000 x 8000 x2
• each operation takes around 0.5 ns => impossible with current
technology
• Need to look to other techniques
#21

22. Space division switching
• Each sample takes a
different path through the
switch, depending on its
destination
• Crossbar: Simplest possible
space-division switch
• Crosspoints can be turned
on or off
#22
i
n
p
u
t
s
outputs

23. Crossbar - example
#23
1
2
3
4
1 2 3 4
sessions: (1,2) (2,4) (3,1) (4,3)
inputs
output

24. Crossbar
• Advantages:
• simple to implement
• simple control
• strict sense non-blocking
• Multicast
• Single source multiple destination ports
• Drawbacks
• number of crosspoints, N2
• large VLSI space
• vulnerable to single faults
#24

25. Time-space switching
• Precede each input trunk in a crossbar with a TSI
• Delay samples so that they arrive at the right time for the space
division switch’s schedule
#25
Crosspoint: 4 (not 16)
memory speed : x2 (not x4)
2 1
4 3
M
U
X
M
U
X
1
2
3
4
TSI
TSI
1 2
4 3
DeMux DeMux

26. Finding the schedule
• Build a routing graph
• nodes - input links
• session connects an input and output nodes.
• Feasible schedule
• Computing a schedule
• compute perfect matching.
#26
1
2
3
4
1
2
3
4

27. Time-Space: Example
#27
2 1
4 3
TSI
2 1
3 4
3
1
2
4
Internal speed = double link speed
time 1
time 2
TSI

28. Internal Non-Blocking Types
• Re-arrangeable
• Can route any permutation from inputs to outputs.
• Strict sense non-blocking
• Given any current connections through the switch.
• Any unused input can be routed to any unused output.
• Wide sense non-blocking.
• There exists a specific routing algorithm, s.t.,
• for any sequence of connections and releases,
• Any unused input can be routed to any unused output,
• assuming all the sequence was served by the routing algorithm.
#29

29. Circuit switching - Space division
• graph representation
• transmitter nodes
• receiver nodes
• internal nodes
• Feasible schedule
• edge disjoint paths.
• cost function
• number of crosspoints (complexity of AxB is AB)
• internal nodes
#30

30. Crossbar - example
#31
1
2
3
4
1 2 3 4

31. Another Example
#32
inputs
outputs

32. Another Example
#33
sessions: (1,3) (2,6) (3,1) (4,4) (5,2) (6,5)
inputs
outputs

33. Clos Network
#34
Clos(N, n , k) : N - inputs/outputs;
cross-points: 2 (N/n)nk + k(N/n)2
nxk (N/n)x(N/n) kxn
N=6
n=2
k=2
3x3
3x3
2x2
2x2
2x2
2x2
2x2
2x2N
k
N/nN/n

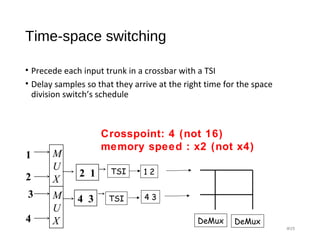
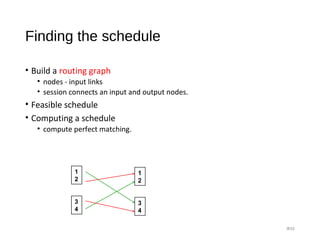
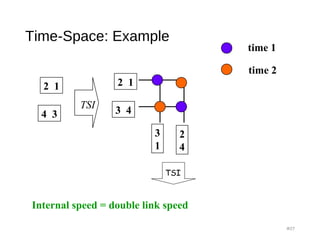
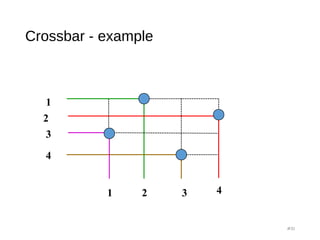
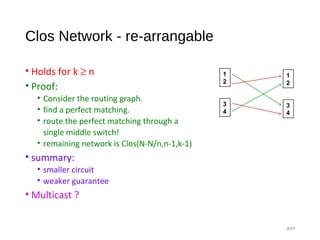
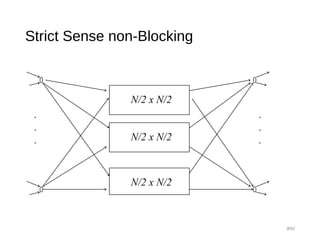
34. Clos Network - strict sense non-blocking
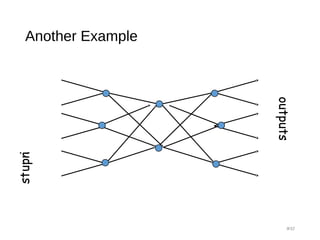
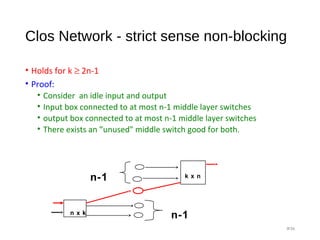
• Holds for k ≥ 2n-1
• Proof Methodology:
• Recall: IF [A,B ⊆ S and |A|+|B| > |S|] then A∩ B≠Ø
• S= The k middle switches
• A = middle switches reachable from the inputs
• B = middle switches reachable from the outputs
• Our case:
• |S|=k
• |A| ≥ k-(n-1)
• |B| ≥ k-(n-1)
#35

35. Clos Network - strict sense non-blocking
• Holds for k ≥ 2n-1
• Proof:
• Consider an idle input and output
• Input box connected to at most n-1 middle layer switches
• output box connected to at most n-1 middle layer switches
• There exists an ”unused" middle switch good for both.
#36
n x k
k x n
n-1
n-1

36. Example
#37
Clos(8,2,3)
N=8
n=2
k=3
4x4
4x4
3x2
3x2
3x2
2x3
2x3
2x3
2x3 4x4 3x2
Need to route a new call

37. Clos Network
#38
nxk (N/n)x(N/n) kxn
N=6
n=2
k=2
3x3
3x3
2x2
2x2
2x2
2x2
2x2
2x2
Why is k=n internally blocking?

38. Clos Network - re-arrangable
• Holds for k ≥ n
• Proof:
• Consider the routing graph.
• find a perfect matching.
• route the perfect matching through a
single middle switch!
• remaining network is Clos(N-N/n,n-1,k-1)
• summary:
• smaller circuit
• weaker guarantee
• Multicast ?
#39
1
2
3
4
1
2
3
4

39. Recursive Construction: basis
#40
The basic element:
The two states:
The dimension: r=0

40. Recursive Construction:
Benes Network
#41
r-1 dimension
N/2 size
r-1 dimension
N/2 size

41. Example 16x16
#42

42. Benes Networks
• Symmetry
• Size:
• F(N) = 2(N/2)*4 + 2F(N/2) = O(N log N)
• Rearrangable
• Clos network with k=2 n=2
• Proof I:
• Build routing graph.
• Find 2 matchings
• route one in the upper Benes and the other in the lower.
#43

43. Greedy permutation routing
• Start with an arbitrary node i1
• set i1 to upper.
• At the output, o1 , a new constraint,
• set o2 to lower.
• Continue until no new constraint.
• Completing a cycle.
• Continue until done.
• Solve for the upper and lower Benes recursively.
#44

44. Example: Benes Network for r=2
#45
level 0 switches level 2r switches
I1
I2
1
2
3
4
5
6
7
8

45. Example
#46
level 0 switches level 2r switches
I1
I2
1
2
3
4
5
6
7
8
1 2 3 4 5 6 7 8
1 5 6 8 4 2 3 7
( )

46. Example
#47
level 0 switches level 2r switches
I1
I2
1
2
3
4
5
6
7
8
1 2 3 4 5 6 7 8
1 5 6 8 4 2 3 7
( )

47. Example
#48
level 0 switches level 2r switches
I1
I2
1
2
3
4
5
6
7
8
1 2 3 4 5 6 7 8
1 5 6 8 4 2 3 7
( )

48. Example
#49
level 0 switches level 2r switches
I1
I2
1
2
3
4
5
6
7
8
1 2 3 4 5 6 7 8
1 5 6 8 4 2 3 7
( )

49. CRS-1 Switch Fabric Overview
#50
1 of 8
2 of 8
8 of 8
1
2
8
1
2
16
40 Gbps
Line Card Line Card
50 Gbps
136 Bytes cells
Fabric
Chassis
100 Gbps/LC(2)
(2.5X Speedup)
1296 x 1296 buffered non-blocking switch
Multi-stage Interconnect—3 Stage Benes topology
S1 S2 S3
S1 S2 S3
S1 S2 S3
2 LEVELS OF PRIORITY
HP Low latency traffic
LP Best effort traffic
MULTICAST SUPPORT
1M multicast groups

50. Basic Router Architecture
#51
3 Main components: Line cards,Switching mechanism,
Route Processor(s), Routing Applications
Control Components
Forwarding Component
Interconnect

51. Strict Sense non-Blocking
#52
N/2 x N/2
N/2 x N/2
.
.
.
.
.
.N/2 x N/2

52. Properties
• Size:
• F(N) = 2N*6 + 3F(N/2) = O( N1.58)
• strict sense non-blocking
• Clos network with k=3 n=2
• Better parameters:
• n=sqrt{N}, k=2sqrt{N}-1
• recursive size sqrt{N} x sqrt{N}
• Circuit size O(N log2.58
N)
#53

53. Cantor Networks
• m copies of Benes network.
• For m = log N its strict sense non-blocking
• Network size N log2
N
• Example
#54

54. Cantor Network
#55
m=4

55. Proof Sketch:
• Benes network:
• 2 log N -1 layers,
• N/2 nodes in layer.
• Middle layer= layer log N -1
• Consider the middle layer of the Benes Networks.
• There are Nm/2 nodes in in all of them combined.
• Bound (from below) the number of nodes reachable from an
input and output.
• If the sum is more than Nm/2:
• There is an intersection
• there has to be a route.
#56

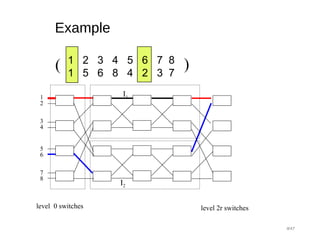
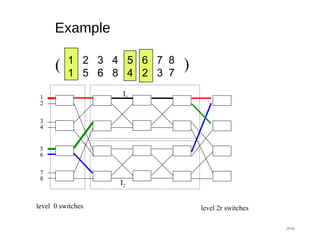
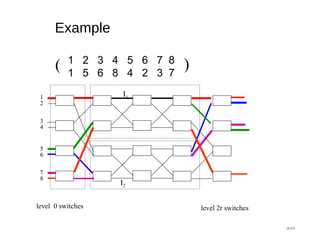
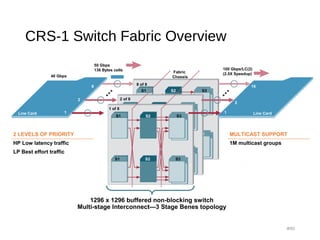
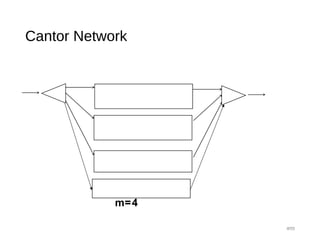
56. Proof Sketch:
• Let A(k) = number of nodes reachable at level k.
• A(0)=m
• A(1)= 2A(0)-1
• A(2)=2A(1)-2
• A(k)=2A(k-1) - 2k-1
= 2k
A(0) - k 2k-1
• A(log N -1) = Nm/2 - (log N -1) N/4
• Need that: 2A(log N -1) > Nm/2.
• 2[Nm/2 - (log N -1) N/4] > Nm/2.
• Hold for m> log N-1.
#57

57. Advanced constructions
• There are networks of size O(N log N).
• the constants are huge!
• Basic paradigm also applies to large packet switches.
#58