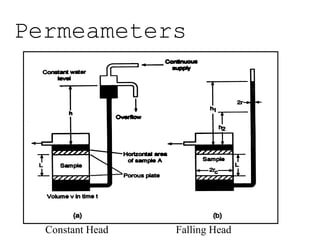
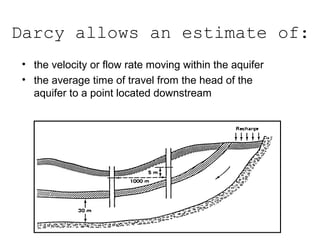
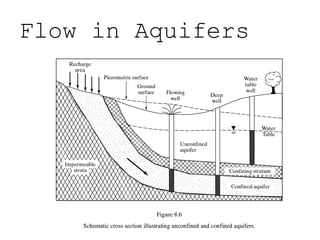
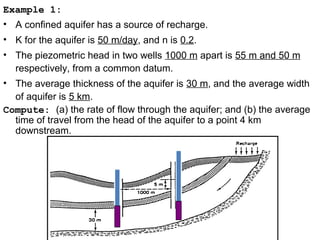
Darcy's law describes groundwater flow through porous media such as aquifers. It states that the flow rate of water is proportional to the hydraulic gradient, which is the change in head over the distance of flow. Specifically, the flow rate is equal to the hydraulic conductivity multiplied by the cross-sectional area available for flow and the hydraulic gradient. Darcy's law provides an accurate description of groundwater flow in most environments and conditions. It can be used to estimate flow velocity, flow rate, and travel time of groundwater through aquifers.

1. Darcy’s Law

2. Darcy allows an estimate of:
• the velocity or flow rate moving within the aquifer
• the average time of travel from the head of the
aquifer to a point located downstream

3. Darcy’s Law
• Darcy’s law provides an
accurate description of the flow
of ground water in almost all
hydrogeologic environments.

4. Flow in Aquifers

5. Darcy’s Experiment (1856):
Flow rate determined by Head loss dh = h1 - h2

6. Darcy’s Law
• Henri Darcy established empirically that
the flux of water through a permeable
formation is proportional to the distance
between top and bottom of the soil
column.
• The constant of proportionality is called the
hydraulic conductivity (K).
• V = Q/A, V α – ∆h, and V α 1/∆L

7. Darcy’s Law
V = – K (∆h/∆L)
and since
Q = VA (A = total area)
Q = – KA (dh/dL)

8. Hydraulic Conductivity
• K represents a measure of the ability for
flow through porous media:
• Gravels - 0.1 to 1 cm/sec
• Sands - 10-2
to 10-3
cm/sec
• Silts - 10-4
to 10-5
cm/sec
• Clays - 10-7
to 10-9
cm/sec

9. Conditions
• Darcy’s Law holds for:
1. Saturated flow and unsaturated flow
2. Steady-state and transient flow
3. Flow in aquifers and aquitards
4. Flow in homogeneous and heterogeneous
systems
5. Flow in isotropic or anisotropic media
6. Flow in rocks and granular media

10. Darcy Velocity
• V is the specific discharge (Darcy velocity).
• (–) indicates that V occurs in the direction of the decreasing
head.
• Specific discharge has units of velocity.
• The specific discharge is a macroscopic concept, and is easily
measured. It should be noted that Darcy’s velocity is different
from the microscopic velocities associated with the actual
paths of individual particles of water as they wind their way
through the grains of sand.
• The microscopic velocities are real, but are probably
impossible to measure.

11. Darcy & Seepage Velocity
• Darcy velocity is a fictitious velocity
since it assumes that flow occurs across
the entire cross-section of the soil
sample. Flow actually takes place only
through interconnected pore channels.
A = total area
Av voids

12. Darcy & Seepage Velocity
• From the Continuity Eqn:
Q = A VD = AV Vs
Where:
Q = flow rate
A = total cross-sectional area of material
AV = area of voids
Vs = seepage velocity
VD = Darcy velocity

13. Darcy & Seepage Velocity
Therefore: VS = VD (A/AV)
Multiplying both sides by the length of the medium (L)
VS = VD ( AL / AVL ) = VD ( VT / VV )
Where:
VT = total volume
VV = void volume
By Definition, Vv / VT = n, the soil porosity
Thus VS = VD / n

14. Example 1:
• A confined aquifer has a source of recharge.
• K for the aquifer is 50 m/day, and n is 0.2.
• The piezometric head in two wells 1000 m apart is 55 m and 50 m
respectively, from a common datum.
• The average thickness of the aquifer is 30 m, and the average width
of aquifer is 5 km.
Compute: (a) the rate of flow through the aquifer; and (b) the average
time of travel from the head of the aquifer to a point 4 km
downstream.

15. The solution
• Cross-Sectional area, A = (30) (5 x 1000) = 15 x 104
m2
• Hydraulic gradient, i = (55-50)/1000 = 5 x 10-3
• Rate of Flow for K = 50 m/day
Q = K.i.A = (50 m/day) (15 x 104
m2
) (5 x 10-3
)
= 37,500 m3
/day
• Darcy Velocity: VD = Q/A
= (37,500 m3
/day) / (15 x 104
m2
)
= 0.25 m/day

16. • Seepage Velocity:
Vs = VD/n = (0.25) / (0.2)
= 1.25 m/day (about 4.1 ft/day)
• Time to travel 4 km downstream:
since, Velocity = Distance/Time
or Time = Distance/Velocity
Time = (4 x1000 m) / (1.25 m/day)
= 3200 days or 8.77 years
• This example shows that water moves very slowly
underground.

17. Limitations of the
Darcian Approach
1. For Reynold’s Number, Re > 10 or where the flow is
turbulent, as in the immediate vicinity of pumped wells.
2. Where water flows through extremely fine-grained
materials (colloidal clay)

18. Confined Aquifer Confining Layer Aquifer
30 ft
Example 2:
• A channel runs almost parallel to a river, and they are 2000 ft apart.
• The water level in the river is at an elevation of 120 ft and 110 ft in the
channel.
• A pervious formation averaging 30 ft thick and with K of 0.25 ft/hr joins them.
• Determine the rate of seepage or flow from the river to the channel.

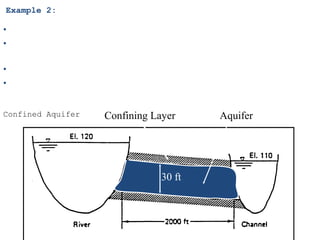
19. • Consider a 1-ft length of river (and channel).
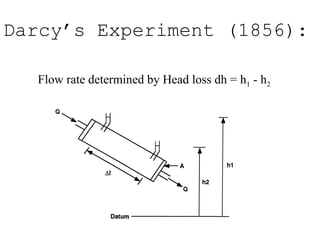
Q = KA [(h1 – h2) / L]
• Where:
A = (30 x 1) = 30 ft2
K
= (0.25 ft/hr) (24 hr/day) = 6 ft/day
• Therefore,
Q = [(6) (30) (120 – 110)] / 2000
= 0.9 ft3
/day/ft length = 0.9 ft2
/day
The solution

20. Permeameters
Constant Head Falling Head

21. Constant head
Permeameter
• Apply Darcy’s Law to find K:
V/t = Q = KA(h/L)
or:
K = (VL) / (Ath)
• Where:
V = volume flowing in time t
A = cross-sectional area of the
sample L = length of sample
h = constant head
t = time of flow