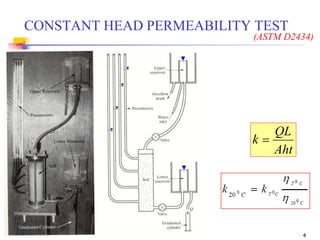
The document discusses geotechnical engineering focusing on water flow through soils, specifically hydraulic conductivity (k) and hydraulic gradient (i). It describes laboratory and field testing methods for determining 'k' including constant and falling head permeability tests, as well as empirical equations for estimating permeability. The document also covers practice problems and factors affecting hydraulic conductivity, such as particle size, void ratio, stratification, saturation, and temperature.

1. 1
Geotechnical Engineering–I [CE-221]
BSc Civil Engineering – 4th Semester
by
Dr. Muhammad Irfan
Assistant Professor
Civil Engg. Dept. – UET Lahore
Email: mirfan1@msn.com
Lecture Handouts: https://groups.google.com/d/forum/2016session-geotech-i
Lecture # 23
20-Apr-2018

2. 2
WATER FLOW THROUGH SOILS
To determine the quantity of flow, two parameters are needed
* k = hydraulic conductivity
* i = hydraulic gradient
Determination of ‘k’
1- Laboratory Testing  [constant head test & falling head test]
2- Field Testing  [constant/falling head tests, pump out tests, etc]
3- Empirical Equations
Determination of ‘i’
1- From the head loss and geometry
2- Flow Nets
(how permeable is the soil medium)
(how large is the driving head)
Today’s
discussion
A
h
kAikq 


L

3. 3
CONSTANT HEAD PERMEABILITY TEST
(ASTM D2434)
 The total volume of collected water may be
expressed as;
Aht
QL
k 
Q = volume of water collected
A = x-sec area of soil specimen
t = duration of water collection
L
h
i  t
L
h
kAQ 






𝑄 = 𝑞 ⋅ 𝑡 = (𝐴𝑣) ⋅ 𝑡 = 𝐴 ⋅ (𝑘𝑖) ⋅ 𝑡

4. 4
Aht
QL
k 
CONSTANT HEAD PERMEABILITY TEST
(ASTM D2434)

5. 5
FALLING/VARIABLE HEAD
PERMEABILITY TEST (ASTM D5084)
 Mainly used for fine-grained soils but can
also be used for coarse-grained soils.
 Procedure is same as constant head test
except:
 Record initial head difference, h1 at
t=0.
 Allow water to flow through the soil
specimen.
 Record the final head difference, h2
at t=t2.
 Record the volume of water, Q (in
ml), collected at the outlet during
this time.

6. 6
FALLING/VARIABLE HEAD
PERMEABILITY TEST (ASTM D5084)
 Rate of flow of water through the specimen at
any time ‘t’ can be given by;
h1 = head at the start of test
h2 = head at the end of test
2
1
log303.2
h
h
At
aL
k 

7. 7
Practice Problem #1
A constant head permeability test on a medium sand sample
having a x-sectional area of 7585mm2 yielded the following data.
Distance between stand pipes = 100 mm
Constant head difference = 70.4 mm
Quantity of water collected = 500 x 103 mm3
Time of collection = 132 sec
Determine the coefficient of permeability of sand specimen.
Aht
QL
k 

8. 8
Practice Problem #2
In a falling head permeability test, a soil sample of 7585mm2
cross-section and 210.2mm length was subjected to a flow of
water from a stand-pipe having cross-sectional area of
730mm2. The stand-pipe level changed from 1650mm to
550mm above reservoir datum during a time interval of 182sec.
Determine the coefficient of permeability of soil.
2
1
log303.2
h
h
At
aL
k 

9. 9
Practice Problem #3
A constant head permeameter, 85 mm in diameter containing a
fine sand sample 450mm long, allowed water to flow at a rate
of 184ml/min under steady-flow conditions. Given the
difference in head between two points 240mm apart was
375mm, determine the coefficient of permeability in mm/sec.
When the same size sample is tested in a falling head
apparatus using a stand-pipe of 32.5mm diameter. Calculate
the time required for the water in the stand-pipe to drop from
1750mm to 1000mm above outflow level to the nearest five
seconds.
Aht
QL
k 
2
1
log303.2
h
h
At
aL
k 

10. 10
DETERMINATION OF ‘k’ –
EMPIRICAL EQUATIONS
Allen Hazen’s Method
Permeability of filter sands
k = C . (D10)2
k = coefficient of permeability (cm/sec)
C = empirical coefficient varying from 90 to 120; typically assumed as 100
D10 = effective size in cm
Applicability → k > 10-3 cm/sec
D10 ranging from 0.1 mm – 3 mm
Cu < 5
Permeability from Consolidation Test
k = CV . mV . γw
Applicability → Clays with k ≤ 10-7 cm/sec

11. 11
DEPENDENCE OF HYDRAULIC
CONDUCTIVITY (k)
1- Effect of Shape and Size of Particles
k = C . (D10)2 Allen Hazen’s equation
i.e., coarser the soil, larger would be permeability
2- Effect of Void Ratio
For sands, the following two equations hold good.
OR
i.e., larger the void ratio, greater would be permeability
2
2
2
1
2
1
e
e
k
k
 3
2
2
1
3
1
2
1 1
1 e
e
e
e
k
k 




12. 12
DEPENDENCE OF HYDRAULIC
CONDUCTIVITY (k)
3- Effect of Stratification
Permeability parallel to the strata > permeability perpendicular to the strata
4- Effect of Degree of Saturation
Sample for permeability test → fully saturated.
Low degree of saturation → low permeability; because entrapped air
blocks water flow
5- Effect of Temperature
Temperature affects viscosity and density of pore fluid
Higher the temperature, higher will be permeability.
Lab tests are standardized at 20°C

13. 13
CONCLUDED
REFERENCE MATERIAL
Principles of Geotechnical Engineering – (7th Edition)
Braja M. Das
Chapter #7 & 8