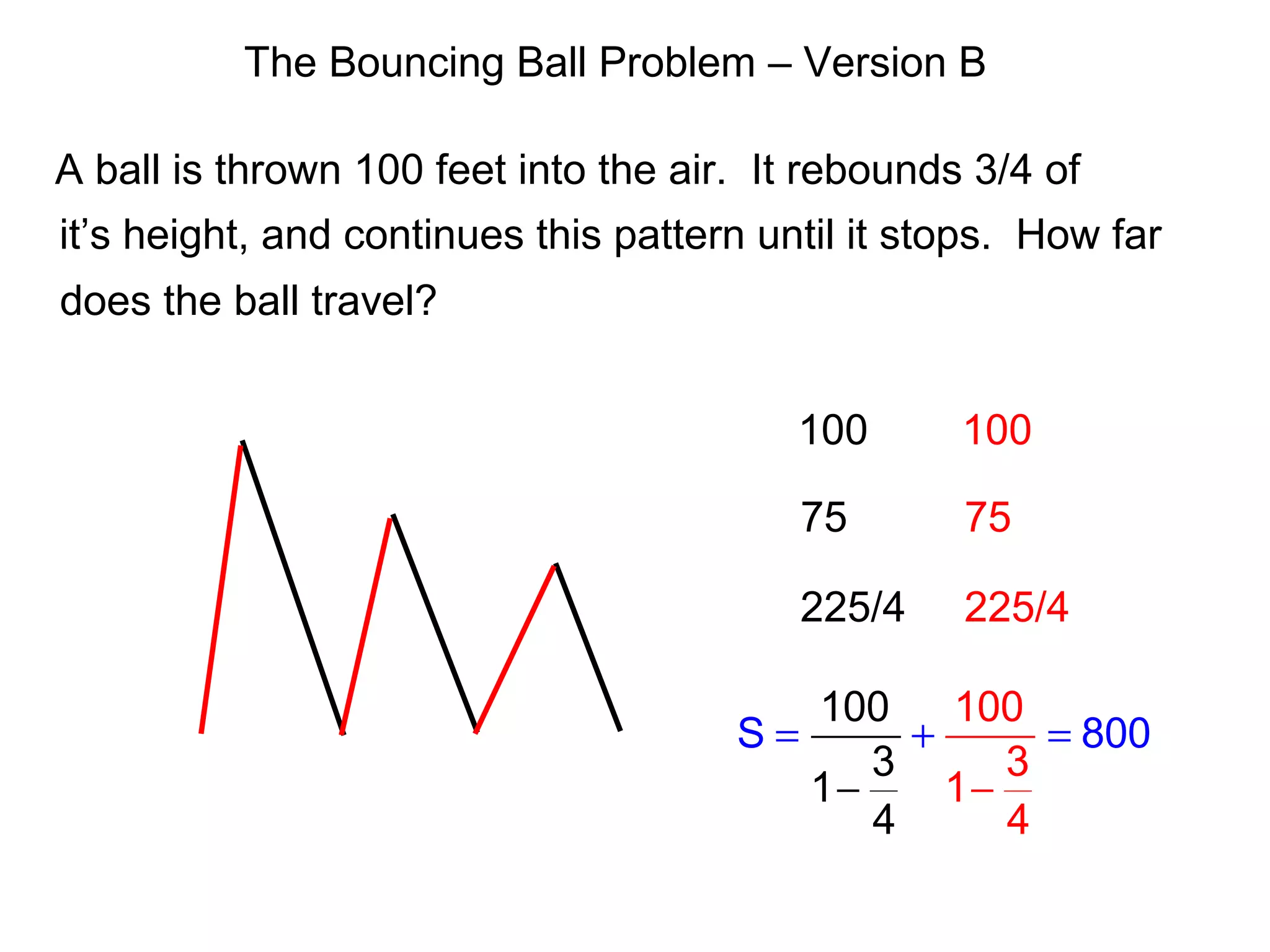
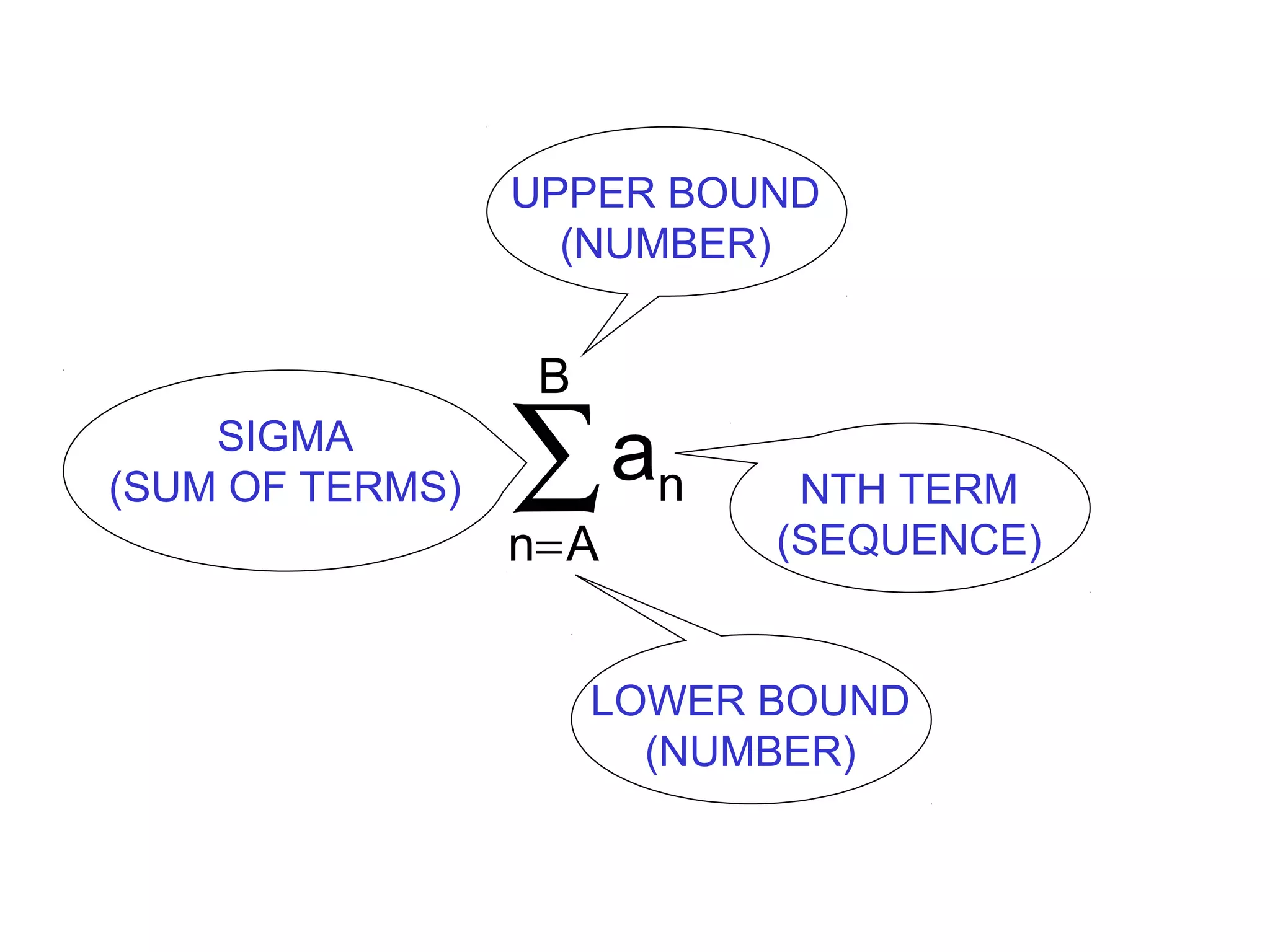
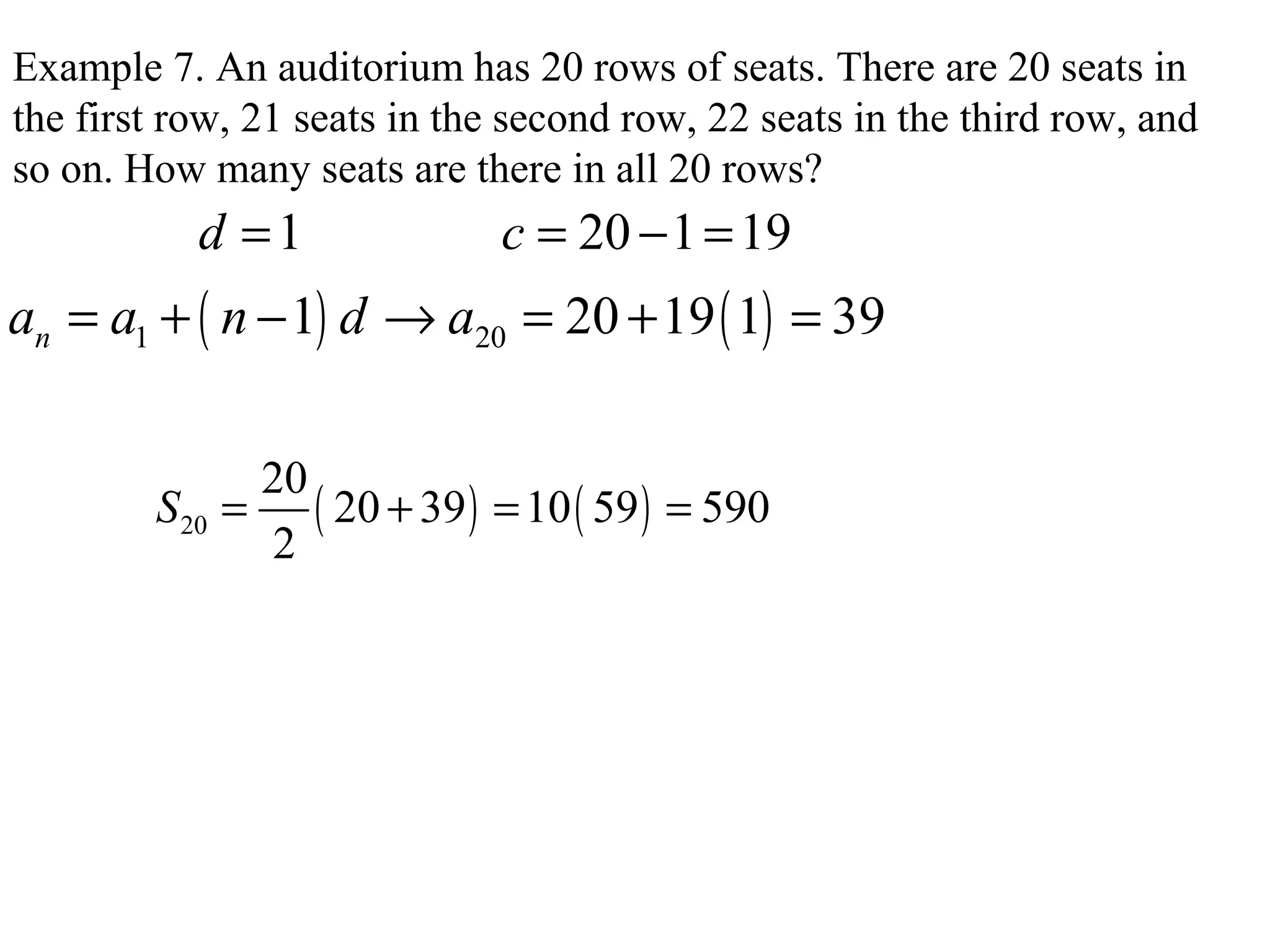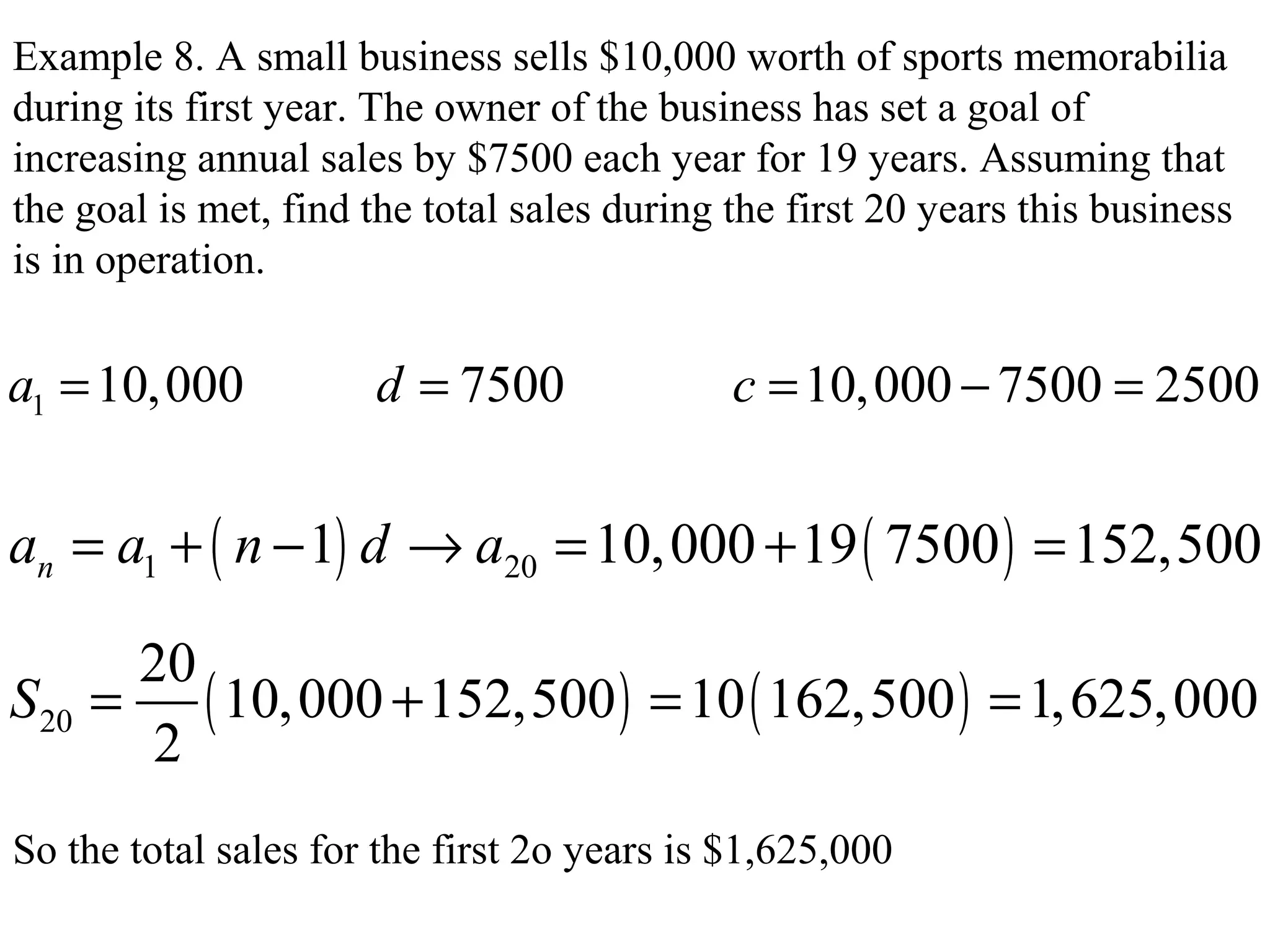This document discusses arithmetic and geometric sequences and series. It provides examples of finding terms in sequences, determining common differences or ratios, and calculating partial sums and infinite sums. Key concepts covered include using formulas to find the nth term, the sum of the first n terms, and determining whether an infinite series has a sum based on the common ratio. Examples demonstrate applying these concepts to problems involving sales projections, seating in an auditorium, and calculating partial sums of sequences.

1. 1

2. 9.2 – Arithmetic Sequences and Series

3. An introduction…………
1, 4, 7,10,13
9,1, 7, 15
6.2, 6.6, 7, 7.4
, 3, 6
− −
π π + π +
Arithmetic Sequences
ADD
To get next term
2, 4, 8,16, 32
9, 3,1, 1/3
1,1/ 4,1/16,1/ 64
, 2.5 , 6.25
− −
π π π
Geometric Sequences
MULTIPLY
To get next term
Arithmetic Series
Sum of Terms
35
12
27.2
3 9
−
π +
Geometric Series
Sum of Terms
62
20/3
85/ 64
9.75π

4. Find the next four terms of –9, -2, 5, …
Arithmetic Sequence
2 9 5 2 7− − − = − − =
7 is referred to as the common difference (d)
Common Difference (d) – what we ADD to get next term
Next four terms……12, 19, 26, 33

5. Find the next four terms of 0, 7, 14, …
Arithmetic Sequence, d = 7
21, 28, 35, 42
Find the next four terms of x, 2x, 3x, …
Arithmetic Sequence, d = x
4x, 5x, 6x, 7x
Find the next four terms of 5k, -k, -7k, …
Arithmetic Sequence, d = -6k
-13k, -19k, -25k, -32k

6. Vocabulary of Sequences (Universal)
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
d common difference→
( )
( )
n 1
n 1 n
nth term of arithmetic sequence
sum of n terms of arithmetic sequen
a a n 1 d
n
S a a
2
ce
= + −
= +
→
→

7. Given an arithmetic sequence with 15 1a 38 and d 3, find a .= = −
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
d common difference→
x
15
38
NA
-3
( )n 1a a n 1 d= + −
( ) ( )38 x 1 15 3= + − −
X = 80

8. 63Find S of 19, 13, 7,...− − −
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
d common difference→
-19
63
??
x
6
( )n 1a a n 1 d= + −
( ) ( )?? 19 6 1
?? 353
3 6= + −
=
−
353
( )n 1 n
n
S a a
2
= +
( )63
63
3 3S
2
19 5−= +
63 1 1S 052=

9. 16 1Find a if a 1.5 and d 0.5= =Try this one:
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
d common difference→
1.5
16
x
NA
0.5
( )n 1a a n 1 d= + −
( )16 1.5 0.a 16 51= + −
16a 9=

10. n 1Find n if a 633, a 9, and d 24= = =
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
d common difference→
9
x
633
NA
24
( )n 1a a n 1 d= + −
( )633 9 21x 4= + −
633 9 2 244x= + −
X = 27

11. 1 29Find d if a 6 and a 20= − =
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
d common difference→
-6
29
20
NA
x
( )n 1a a n 1 d= + −
( )120 6 29 x= + −−
26 28x=
13
x
14
=

12. Find two arithmetic means between –4 and 5
-4, ____, ____, 5
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
d common difference→
-4
4
5
NA
x
( )n 1a a n 1 d= + −
( ) ( )15 4 4 x= + −−
x 3=
The two arithmetic means are –1 and 2, since –4, -1, 2, 5
forms an arithmetic sequence

13. Find three arithmetic means between 1 and 4
1, ____, ____, ____, 4
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
d common difference→
1
5
4
NA
x
( )n 1a a n 1 d= + −
( ) ( )4 1 x15= + −
3
x
4
=
The three arithmetic means are 7/4, 10/4, and 13/4
since 1, 7/4, 10/4, 13/4, 4 forms an arithmetic sequence

14. Find n for the series in which 1 na 5, d 3, S 440= = =
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
d common difference→
5
x
y
440
3
( )n 1a a n 1 d= + −
( )n 1 n
n
S a a
2
= +
( )y 5 31x= + −
( )
x
40 y4
2
5= +
( )( )1
2
x
440 5 5 x 3= + + −
( )x 7 x
440
2
3
=
+
( )880 x 7 3x= +
2
0 3x 7x 880= + −
X = 16
Graph on positive window

15. The sum of the first n terms of an infinite sequence
is called the nth partial sum.
1( )
2n n
nS a a= +

16. Example 6. Find the 150th
partial sum of the arithmetic sequence, 5,
16, 27, 38, 49, …
1 5 11 5 11 6a d c= = → = − = −
11 6na n= − ( )150 11 150 6 1644a→ = − =
( ) ( )150
150
5 1644 75 1649 123,675
2
S = + = =

17. Example 7. An auditorium has 20 rows of seats. There are 20 seats in
the first row, 21 seats in the second row, 22 seats in the third row, and
so on. How many seats are there in all 20 rows?
1 20 1 19d c= = − =
( ) ( )1 201 20 19 1 39na a n d a= + − → = + =
( ) ( )20
20
20 39 10 59 590
2
S = + = =

18. Example 8. A small business sells $10,000 worth of sports memorabilia
during its first year. The owner of the business has set a goal of
increasing annual sales by $7500 each year for 19 years. Assuming that
the goal is met, find the total sales during the first 20 years this business
is in operation.
1 10,000 7500 10,000 7500 2500a d c= = = − =
( ) ( )1 201 10,000 19 7500 152,500na a n d a= + − → = + =
( ) ( )20
20
10,000 152,500 10 162,500 1,625,000
2
S = + = =
So the total sales for the first 2o years is $1,625,000

19. 9.3 – Geometric Sequences and Series

20. 1, 4, 7,10,13
9,1, 7, 15
6.2, 6.6, 7, 7.4
, 3, 6
− −
π π + π +
Arithmetic Sequences
ADD
To get next term
2, 4, 8,16, 32
9, 3,1, 1/3
1,1/ 4,1/16,1/ 64
, 2.5 , 6.25
− −
π π π
Geometric Sequences
MULTIPLY
To get next term
Arithmetic Series
Sum of Terms
35
12
27.2
3 9
−
π +
Geometric Series
Sum of Terms
62
20/3
85/ 64
9.75π

21. Vocabulary of Sequences (Universal)
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
r common ratio→
( )
n 1
n 1
n
1
n
nth term of geometric sequence
sum of n terms of geometric sequ
a a r
a r 1
S
r 1
ence
−
→ =
 − =
−
→

22. Find the next three terms of 2, 3, 9/2, ___, ___, ___
3 – 2 vs. 9/2 – 3… not arithmetic
3 9/ 2 3
1.5 geometric r
2 3 2
= = → → =
3 3 3 3 3 3
2 2 2
9
2, 3, , , ,
2
9 9 9
2 2 2 2 2 2
× × × × × ×
9
2, 3, , ,
27 81 243
4 8
,
2 16

23. 1 9
1 2
If a ,r , find a .
2 3
= =
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
r common ratio→
1/2
x
9
NA
2/3
n 1
n 1a a r −
=
9 1
1 2
x
2 3
−
  
=   
  
8
8
2
x
2 3
=
×
7
8
2
3
=
128
6561
=

24. Find two geometric means between –2 and 54
-2, ____, ____, 54
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
r common ratio→
-2
54
4
NA
x
n 1
n 1a a r −
=
( ) ( )
14
54 2 x
−
−=
3
27 x− =
3 x− =
The two geometric means are 6 and -18, since –2, 6, -18, 54
forms an geometric sequence

25. 2 4 1
2
Find a a if a 3 and r
3
− = − =
-3, ____, ____, ____
2
Since r ...
3
=
4 8
3, 2, ,
3 9
− −
− −
2 4
8 10
a a 2
9 9
− − 
− = − − = 
 

26. 9Find a of 2, 2, 2 2,...
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
r common ratio→
x
9
NA
2
2 2 2
r 2
22
= = =
n 1
n 1a a r −
=
( )
9 1
x 2 2
−
=
( )
8
x 2 2=
x 16 2=

27. 5 2If a 32 2 and r 2, find a= = −
____, , ____,________ ,32 2
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
r common ratio→
x
5
NA
32 2
2−
n 1
n 1a a r −
=
( )
5 1
32 2 x 2
−
−=
( )
4
32 2 x 2= −
32 2 x4=
8 2 x=

28. *** Insert one geometric mean between ¼ and 4***
*** denotes trick question
1
,____,4
4
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
r common ratio→
1/4
3
NA
4
x
n 1
n 1a a r −
=
3 11
4
4
r −
= 2
r
1
4
4
→ = 2
16 r→ = 4 r→ ± =
1
,1, 4
4
1
, 1, 4
4
−

29. 7
1 1 1
Find S of ...
2 4 8
+ + +
1a First term→
na nth term→
nS sum of n terms→
n number of terms→
r common ratio→
1/2
7
x
NA
11
184r
1 1 2
2 4
= = =
( )n
1
n
a r 1
S
r 1
 − =
−
7
1 1
2 2
x
1
2
1
1
   
−        =
−
7
1 1
2 2
1
2
1
   
−        =
−
63
64
=

30. Section 12.3 – Infinite Series

31. 1, 4, 7, 10, 13, …. Infinite Arithmetic No Sum
3, 7, 11, …, 51 Finite Arithmetic ( )n 1 n
n
S a a
2
= +
1, 2, 4, …, 64 Finite Geometric
( )n
1
n
a r 1
S
r 1
−
=
−
1, 2, 4, 8, … Infinite Geometric
r > 1
r < -1
No Sum
1 1 1
3,1, , , ...
3 9 27
Infinite Geometric
-1 < r < 1
1a
S
1 r
=
−

32. Find the sum, if possible:
1 1 1
1 ...
2 4 8
+ + + +
1 1
12 4r
11 2
2
= = = 1 r 1 Yes→ − ≤ ≤ →
1a 1
S 2
11 r
1
2
= = =
−
−

33. Find the sum, if possible: 2 2 8 16 2 ...+ + +
8 16 2
r 2 2
82 2
= = = 1 r 1 No→ − ≤ ≤ →
NO SUM

34. Find the sum, if possible:
2 1 1 1
...
3 3 6 12
+ + + +
1 1
13 6r
2 1 2
3 3
= = = 1 r 1 Yes→ − ≤ ≤ →
1
2
a 43S
11 r 3
1
2
= = =
−
−

35. Find the sum, if possible:
2 4 8
...
7 7 7
+ + +
4 8
7 7r 2
2 4
7 7
= = = 1 r 1 No→ − ≤ ≤ →
NO SUM

36. Find the sum, if possible:
5
10 5 ...
2
+ + +
5
5 12r
10 5 2
= = = 1 r 1 Yes→ − ≤ ≤ →
1a 10
S 20
11 r
1
2
= = =
−
−

37. The Bouncing Ball Problem – Version A
A ball is dropped from a height of 50 feet. It rebounds 4/5 of
it’s height, and continues this pattern until it stops. How far
does the ball travel?
50
40
32
32/5
40
32
32/5
40
S 45
50
4
1
0
1
55
4
= =
−
+
−

38. The Bouncing Ball Problem – Version B
A ball is thrown 100 feet into the air. It rebounds 3/4 of
it’s height, and continues this pattern until it stops. How far
does the ball travel?
100
75
225/4
100
75
225/4
10
S 80
100
4 4
3
1
0
1
0
3
= =
−
+
−

39. Sigma Notation

40. B
n
n A
a
=
∑
UPPER BOUND
(NUMBER)
LOWER BOUND
(NUMBER)
SIGMA
(SUM OF TERMS) NTH TERM
(SEQUENCE)

41. ( )
j
4
1
j 2
=
+∑ ( )21= + ( )2 2+ + ( )3 2+ + ( )24+ + 18=
( )
7
4a
2a
=
∑ ( )( )42= ( )( )2 5+ ( )( )2 6+ ( )( )72+ 44=
( )n
n 0
4
0.5 2
=
+∑ ( )0
0.5 2= + ( )1
0.5 2+ + ( )2
0.5 2+ + ( )3
0.5 2+ + ( )4
0.5 2+ +
33.5=

42. 0
n
b
3
6
5=
∞
 
= 
 
∑
0
3
6
5
 
 
 
1
3
6
5
 
+  
 
2
3
6
5
 
+  
 
...+
1a
S
1 r
=
−
6
15
3
1
5
= =
−
( )
2
x
3
7
2x 1
=
+∑ ( )( ) ( )( ) ( )( ) ( )( )2 1 2 8 1 2 9 1 ...7 2 123= + + + + + + + +
( ) ( )n 1 n
2n 1
S a a 15
2
3
2
7
47
− +
= + = + 527=

43. ( )
1
b
9
4
4b 3
=
+∑ ( )( ) ( )( ) ( )( ) ( )( )4 3 4 5 3 4 6 3 ...4 4 319= + + + + + + + +
( ) ( )n 1 n
1n 1
S a a 19
2
9
2
4
79
− +
= + = + 784=

44. Rewrite using sigma notation: 3 + 6 + 9 + 12
Arithmetic, d= 3
( )n 1a a n 1 d= + −
( )na 3 n 1 3= + −
na 3n=
4
1n
3n
=
∑

45. Rewrite using sigma notation: 16 + 8 + 4 + 2 + 1
Geometric, r = ½
n 1
n 1a a r −
=
n 1
n
1
a 16
2
−
 
=  
 
n 1
n
5
1
1
16
2
−
=
 
 
 
∑

46. Rewrite using sigma notation: 19 + 18 + 16 + 12 + 4
Not Arithmetic, Not Geometric
n 1
na 20 2 −
= −
n 1
n
5
1
20 2 −
=
−∑
19 + 18 + 16 + 12 + 4
-1 -2 -4 -8

47. Rewrite the following using sigma notation:
3 9 27
...
5 10 15
+ + +
Numerator is geometric, r = 3
Denominator is arithmetic d= 5
NUMERATOR: ( )
n 1
n3 9 27 ... a 3 3
−
+ + + → =
DENOMINATOR: ( )n n5 10 15 ... a 5 n 1 5 a 5n+ + + → = + − → =
SIGMA NOTATION:
( )
1
1
n
n 5n
3 3
−
∞
=
∑

48. 48
Do you find this slides were useful?
One second of your life , can bring a smile in a girl life
If Yes ,Join Dreams School “Campaign for Female Education”
Help us in bringing a change in a girl life, because “When
someone takes away your pens you realize quite how
important education is”.
Just Click on any advertisement on the page, your one
click can make her smile.
Eliminate Inequality “Not Women”
One second of your life , can bring a smile in her life!!
Do you find these slides were useful?
If Yes ,Join Dreams School “Campaign
for Female Education”
Help us in bringing a change in a girl life,
because “When someone takes away your
pens you realize quite how important
education is”.
Just Click on any advertisement on the page,
your one click can make her smile.
We our doing our part & u ?
Eliminate Inequality “Not Women”