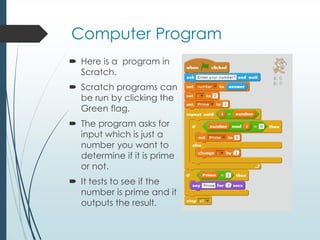
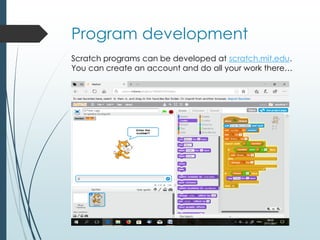
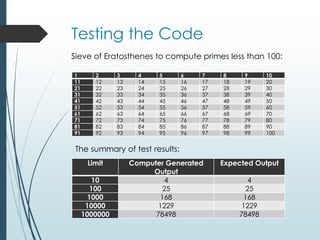
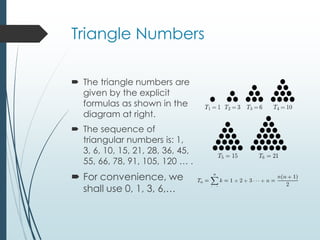
This document provides instructions and materials for a course project on solving problems using computer programming. It includes two problems - counting prime numbers below 10,000 and counting triangular numbers below 1,000,000. Algorithms are presented for both problems using pseudocode. Students are instructed to implement the algorithms in Scratch or another programming language. Sample Scratch and Python programs are included, along with testing to validate the outputs against known results. The document aims to help students learn programming skills through solving mathematical problems.

1. Course Project Solutions
Discrete Mathematics 2018

2. Requirements
 This Mini-Project will give you a chance to
see how you can use computer languages
to solve problems.
 I recommend Scratch because it is the most
accessible language and is available online
at scratch.mit.edu.
 You don't have to use Scratch and any
other programming language with which
you are familiar will work just as well.
 Take advantage of this opportunity to learn.

3. Problem 1
 A prime number is a number greater
than 1 which is only divisible by itself and
1. Thus, 2, 3, 5 etc are prime numbers. To
determine if a number is prime we just
have to determine if it is divisible by any
integer less than itself.
Produce a program that counts the
number of primes less than 10000.

4. Algorithm
 To solve the problem, you would need to
develop an algorithm to count the number
of primes less than 1000000.
 Google the internet to see if you can find a
suitable algorithm, or better still come up
with one of your own design.
 You can use this as a base for developing
your own algorithm and program to solve
the problem. It should be obvious what the
algorithm is doing.
 You still have to test it using a dry run
anyway.

5. Program notes
 This algorithm uses a flag
 We shall use Prime = 1 to denote that we have a
prime and Prime = 0 to denote Not a prime. Scratch
does not have Boolean variables so we have to make
them up!
 Also, we make use of subprocedures or rather a
function called CheckPrime which takes a parameter
number and checks if this is Prime.
 If it is, then it adds it onto a list of Primes
 Finally, we can just output the length of the list of
Primes
 We want to count the number of primes less thana
given number

6. Algorithm
CheckPrime: To determine if a given number is prime
Input your number
Set i to 2
# Assume number is prime unless we prove otherwise
Set Prime to 1
# Check to see if it is divisible by any smaller number
Repeat until i = number
If number mod i = 0 then
Set Prime to 0
Else increment i
If Prime = 1 then
Output number is Prime

7. Dry Run
At this point, you should have a dry
run to test your algorithm to see if it
is doing what you intended it to
do…
In the dry run you follow the
execution line by line through the
algorithm until you obtain the
output.

8. Computer Program
 Here is a program in
Scratch.
 Scratch programs can
be run by clicking the
Green flag.
 The program asks for
input which is just a
number you want to
determine if it is prime
or not.
 It tests to see if the
number is prime and it
outputs the result.

9. Program development
Scratch programs can be developed at scratch.mit.edu.
You can create an account and do all your work there…

10. Try it yourself
Try creating this project in
Scratch. It is most educational.
You will enjoy the experience.

11. Program Solution
In this solution, the
program makes use of a
procedure called
CheckPrime which is
called by the main
program as shown below:

12. Testing
Once you have your program, first find the
number of primes less than 10, and then less than
100 and by using this sieve check to see if your
program is returning the correct answers.
Once you are satisfied, you can enter higher limits
and hopefully your program will work for the limit
100000 as per required.
If possible, add a timer to see how long your
program takes to run each of the tests and graph
the result. From your graph, project how long it
would take to compute the result for n = 106.

13. Testing the Code
Limit Computer Generated
Output
Expected Output
10 4 4
100 25 25
1000 168 168
10000 1229 1229
1000000 78498 78498
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
Sieve of Eratosthenes to compute primes less than 100:
The summary of test results:

14. Conclusion
 We were asked to produce a program
that counts the number of primes less than
10000.
 From the results obtained and the testing
it appears that the program is outputting
the result which is the number of primes
less than the limit.
 The number of primes less than 10000 is
1229. The program can also produce
counts higher than for the limit 10000
without causing any overflow.

15. Problem 2
 Over the years, it has become very fascinating to
discover the various types of numbers and to explore
their uniqueness. One such type of numbers is the set of
triangular numbers.
 A triangular number or triangle number counts the
objects that can form an equilateral triangle, as in the
diagram.
 The nth triangle number is the number of dots composing
a triangle with n dots on a side, and is equal to the sum
of the n natural numbers from 1 to n.
 The problem is to determine how many of these
numbers there are that are less than 1000000 just as
you did for the primes.

16. Triangle Numbers
 The triangle numbers are
given by the explicit
formulas as shown in the
diagram at right.
 The sequence of
triangular numbers is: 1,
3, 6, 10, 15, 21, 28, 36, 45,
55, 66, 78, 91, 105, 120 … .
 For convenience, we
shall use 0, 1, 3, 6,…

17. Algorithm
Input UpperLimit
set n to 1
Set number to 0 // as pointed out in the specification
Create an empty list of Triangle numbers
repeat until number > UpperLimit
if number < UpperLimit
add number to TriangleNumberslist
set number to n * (n + 1)/2
increment n
Output count of TriangleNumbers list

18. Dry Run
You need a dry run for the algorithm
here to make sure it is doing what
you want it to do and giving you the
results, you expect.
Basically, it sets the upper limit,
checks to see if the number is a
triangular number and adds it in if it
is. Finally, it outputs the count.

19. Check out this algorithm…
Go through step by step to see if it
is actually doing what it is
supposed to do.
Try to follow the next slide.
We would need to run it up to an
UpperLimit of say 5 to convince
ourselves of its correctness.

20. Dry Run
UpperLimit = 5
Code n n(n + 1)/2 number TriNum count Output
Set n to 1, number to
zero, count to 0
1 0 [] 0
Add number to
TriNums
[0]
Set number to
n(n+1)/2
1 1
Increment n 2
Add number to
TriNums
[0, 1]
Set number to
n(n + 1)/2
3
Add number to
TriNums
[0, 1, 3]
Increment n 3
Set number to
n(n + 1)/2
6 [0,1, 3]
Number is greater than UpperLimit so drops out of loop.

21. Scratch Program
 The Scratch program starts
at the click of the Green
flag
 It sets the upper limit, using
the variable Upper Limit.
 It initialises the variables n,
number and count, and
iterates the variable number
while less than the limit.
 It checks to see if the
number is a triangular
number and adds it in if it is.
 Finally, it counts the number
of elements in the Triangle
Numbers list.

22. To get started…
Create New Project
Click on Controls and insert the starting control (Green
Flag)…

23. Variables
 Variables are temporary locations in
memory which you can assign values…
 We have already created several
variables including: n, UpperLimit,
answer, etc
 Use meaningful names for the variable
identifiers

24. Continuing…
Create a new list called TriNums, which we shall use to
store the Triangle Numbers and clear it.
Your control construct is a repeat until block as shown
inside which we have nested an if-then construct. As you
build the program you can use the controls at right to run
and stop as required.

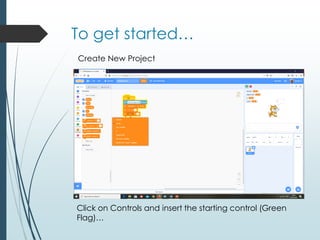
25. Program Run with n = 5
Notice the output on the right hand side. With the
UpperLimit as 5 we have the list [0, 1, 3] as per the dry
run.

26. Shared Program
 This program is shared at Scratch so you can see it at:
 https://scratch.mit.edu/projects/374487361/

27. Python Program
# Triangle numbers less than 10000
limit = 100
# Initialise loop counter
i = 1
trinum = 1
# The i th triangular number is i * (i + 1)/2
while trinum < limit:
trinum = i * (i + 1) / 2
i = i + 1
count = i - 1
print "count = ", count
Here is the Python code…

28. Testing
limit Expected output Computer output
100 14 14
1000 45 45
10000 141 141
1000000 1413 1413
We input 10 and see if the program outputs3. Then
input 100 and see if the program outputs 14 which is
the result we obtained from an alternative count. We
do the same for 1000. If the program outputs the
answer, we can trust it and assume it works for
1000000.

29. Conclusion
 We designed this program for numbers 0, 1, 3, 6
etc. You could try to see if you could arrange for
it to print out the list as we initially wanted it.
 From the results of the testing using lower
limits, it appears that the program is
computing the count of the triangle
numbers less than the limit.
 We were asked for the count of the triangle
numbers less than 1000000 and the answer is
1413.