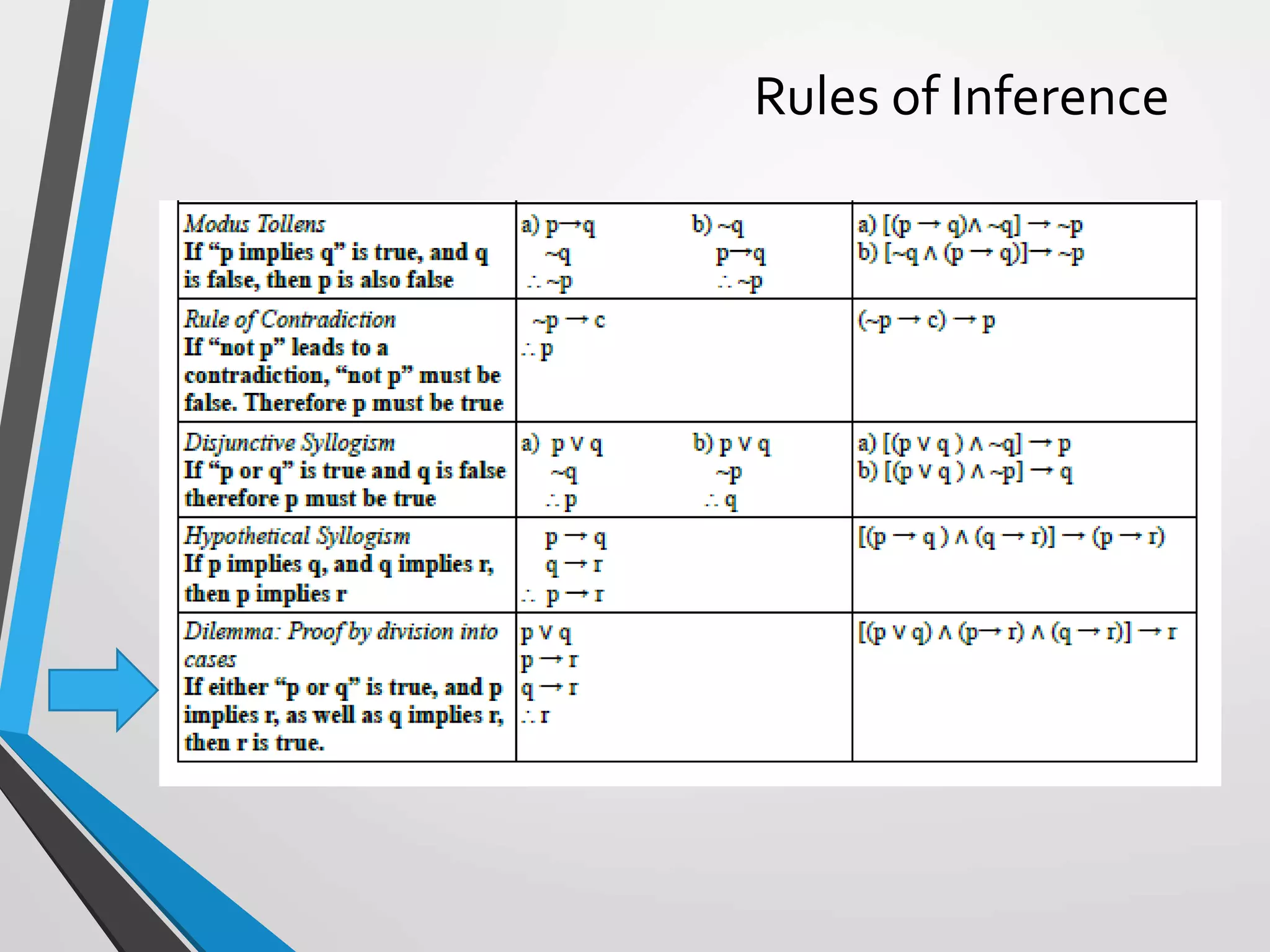
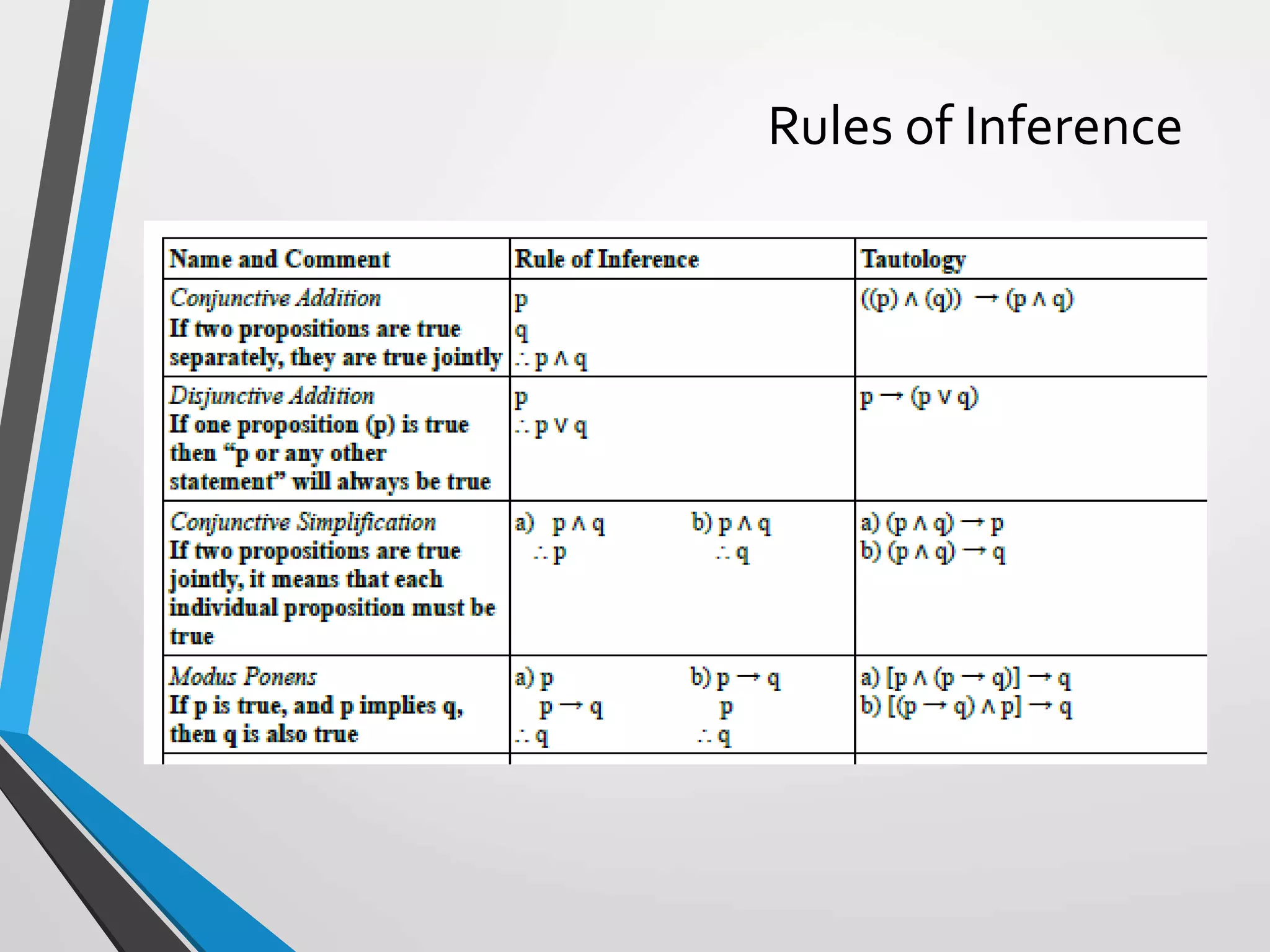
Arguments and methods of proof

Arguments
&
Methods of Proof
Discrete Mathematics

What is an Argument?
An argument is a series of propositions or
statements that end with a conclusion.These
propositions, also called hypotheses or
premises, if true, build inevitably and
necessarily to the stated conclusion.
When the conditions are satisfied, we have
what is called a valid (deductive) argument.

Consider…
If there is cream, then I will drink
coffee. If there is a donut, then I will
drink coffee.There is no cream and
there is a donut.
Therefore, I drink coffee.

Again…
If there is cream, then I will drink
coffee.
If there is a donut, then I will drink
coffee.
There is no cream and there is a donut.
Therefore, I drink coffee.

Formulating the Argument
• Premises
• If there is cream, then I will drink coffee.
• If there is a donut, then I will drink coffee,
• There is no cream and there is a donut.
• Conclusion
• I will drink coffee

Symbolically, we have…
• Premises
• If p [there is cream], then q [I will drink coffee].
• If r [there is a donut], then q [I will drink coffee],
• ~p [There is no cream] and r [there is a donut].
• Conclusion
• q [I will drink coffee].
and the argument format is:
p → q
r → q
~p ∧ r
--------
q
p: there is cream
q: I will drink coffee
r: there is a donut

Analysing the argument with aTruthTable
p q r p → q r → q ~p ~p ∧ r (p → q) ∧ (r → q) ∧ (~p ∧ r) ANDED → q
F F F T T T F F T
F F T
F T F

Valid Argument
A valid argument is an argument
where, if the premises are true,
then the conclusion must be
true.
A form of argument which is not
valid is called a fallacy.

Operational method ofValidation of an Argument
Form a truth table in which the premises
are columns and the conclusion is the last
column.
Star every row in which the premises are
true.
Declare the argument valid if every starred
row has aT in the last column.
Once we have verified an argument, we never
have to question its validity again.

Analysing the argument with aTruthTable
p q r p → q r → q ~p ~p ∧ r (p → q) ∧ (r → q) ∧ (~p ∧ r) ANDED → q
F F F T T T F F T
F F T T F T T F T
F T F T T T F F T
F T T T T T T T T
T F F F T F F F T
T F T F F F F F T
T T F T T F F F T
T T T T T F F F T
This is a valid argument.

Consider the argument…
If you have a valid password, then you
can log on to the network.You have a
valid password.
You can log on to the network.

Consider the argument…
can log on to the network.
You have a valid password.

Symbolic representation…
can log on to the network.You have a
valid password.
p:You have a valid password
q:You can log on to the network

Argument form…
If you have a valid password, then you can log on to the
network.You have a valid password.
p:You have a valid password
q:You can log on to the network
Argument form
p → q
P
--------
q
We can write the argument as: [p ∧ (p → q) ] → q

Assessing validity of [p ∧ (p → q)] → q
p q p → q p ∧ (p → q) [p ∧ (p → q)] → q
F F T F T
F T T F T
T F F F T
T T T T T
The last row is where p =T and p → q =T and the argument implication is
T and so the argument is valid. It is a tautology so it is valid anyway.
•This argument form is called modus
ponens and is a valid argument.

Tautologies
Any argument with a tautology as the
conclusion is valid, no matter what the
premises are.
Validity is a technical term in formal logic
meaning that the conclusion cannot fail to be
true if the premises are true. Since a
tautology is always true it follows for such an
argument that the conclusion can not fail to
be true if the premises are true.

Another Example
If you are a Reggae lover then you know Bob Marley.
Jessica is a Reggae lover.
Therefore, Jessica knows Bob Marley.

Symbolic Representation
If you are a Reggae lover then you know Bob Marley.
Jessica is a Reggae lover.
Therefore, Jessica knows Bob Marley.
This argument can be condensed symbolically:
If p then q;
p;
therefore q.

p q p → q p ∧ (p → q) [p ∧ (p → q)] → q
F F T F T
F T T F T
T F F F T
T T T T T
•It is a valid argument. Do you recognise
the argument form?
*

p q p → q p ∧ (p → q) [p ∧ (p → q)] → q
F F T F T
F T T F T
T F F F T
T T T T T
• It is a valid argument. Do you recognise the
argument form?
• Remember we had called this modus ponens.
• We need to be able to recall the argument form as
we can simply quote that to determine whether
an argument is valid or not.
*

Another argument…
You can’t log on to the network.
If you have a valid password, you can
log on to the network.
You do not have a current password.

Argument form…
￢qYou can’t log on to the network.
If p:you have a valid password, then q you can log on
to the network.
￢p You do not have a current password.
p → q
￢ q
----------
￢ p
We can write this in shorthand as: [(p → q) ∧ ￢ q] → ￢ p

Assessing the argument form using a truth table
p q p → q ￢p ￢q (p → q) ∧ ￢q [(p → q) ∧ ￢q] → ￢p
F F
F T
T F
T T

Is it a valid argument?
p q p → q ￢p ￢q (p → q) ∧ ￢q [(p → q) ∧ ￢q] → ￢p
F F T T T T T
F T T T F F T
T F F F T F T
T T T F F F T
*

Is it a valid argument?
It is a valid argument.This
argument f0rm is called
modus tollens.
p q p → q ￢p ￢q (p → q) ∧ ￢q [(p → q) ∧ ￢q] → ￢p
F F T T T T T
F T T T F F T
T F F F T F T
T T T F F F T

StarWars
If Mr. Scott is still with us, then the power
will come on.The power comes on.
Therefore, Mr. Scott is still with us.
Valid or
Invalid?

Assign Logical variables
If p [Mr. Scott is still with us], then
q [the power will come on].
q [The power comes on].
Therefore, p [Mr. Scott is still with us].

Argument form
If p [Mr. Scott is still
with us], then q [the
power will come on]. q
[The power comes on].
Therefore, p [Mr. Scott
is still with us].
p → q
q
----------
p
This is a case of affirming the consequent
of a conditional and concluding that the
antecedent is true.

Assessing validity of [(p → q) ∧ q ] → p
p q p → q (p → q) ∧ q [(p → q) ∧ q]→ p
F F T F T
F T T T F
T F F F T
T T T T T
•Is this a valid argument?
*
*

Argument form
If p [Mr. Scott is still
with us], then q [the
power will come on]. q
[The power comes on].
Therefore, p [Mr. Scott
is still with us].
p → q
q
----------
p
This is a case of affirming the consequent of a
conditional and concluding that the antecedent is
true, The argument form is [(p → q) ∧ q] → p but
this is NOT a valid argument.

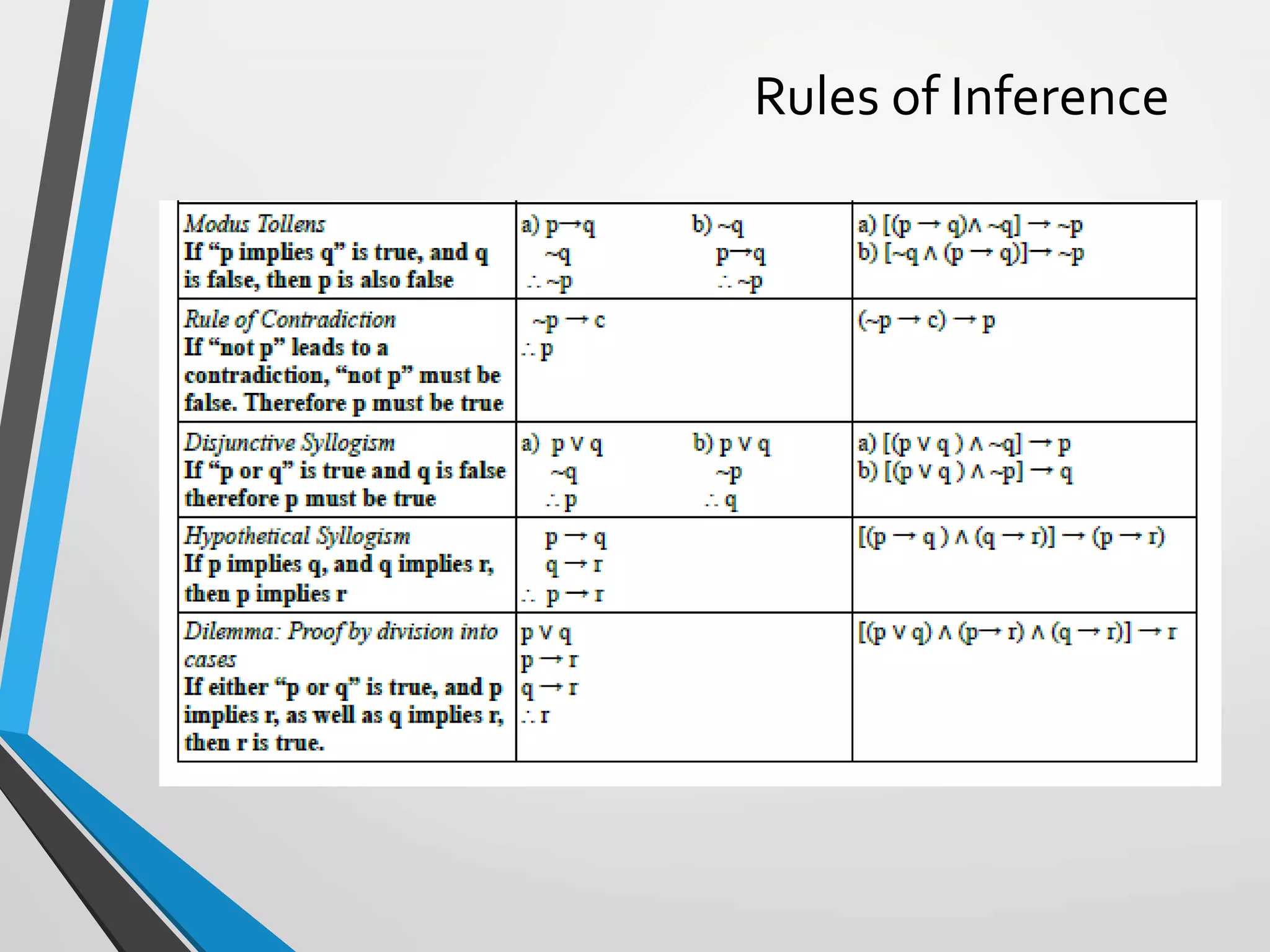
Rules of Inference
A rule of inference is any valid argument.
Page 21 of the Unit notes gives you all
the rules of inference.We have already
seen and proven two important ones –
modus ponens and modus tollens. Of
course ther are others as you cans ee
there!

What is a Proof?
A proof is a demonstration, or
argument, that shows beyond a
shadow of a doubt that a given
assertion is a logical consequence of
our axioms and definitions.

Kurt Godel
Kurt Godel, a brilliant mathematician and logician born and
raised in Czechoslovakia in 1906, earned his Ph.D at the
University ofVienna.
In 1931 he produced a work regarded as the single greatest
piece in mathematical logic: “On formally undecidable
proposition of Principia Mathematica and related systems I”
(originally in German). In it he showed that the German
mathematician David Hilbert’s (1862 – 1943) aim of formalizing
mathematics and demonstrating it to be complete (all facts can
be proved), consistent (nothing false can be proved) and
decidable (all propositions can be shown to be either true or
false) was unattainable.

Axiom
An axiom is a statement or proposition
which is regarded as being established,
accepted, or self-evidently true without
proof.

Direct Proof
A direct proof is a mathematical
argument that uses rules of
inference to derive the conclusion
from the premises.

Example
Prove the Disjunctive Syllogism by
using a Chain of Inferences.

Example
Prove the Disjunctive Syllogism by
using a Chain of Inferences.
So, we might ask, what is the
Disjunctive Syllogism?

Example
Prove the Disjunctive Syllogism by using a
Chain of Inferences.
So, we might ask, what is the Disjunctive
Syllogism?
It is the argument form: (p ∨ q) ∧ ￢p → q
found on p 21 of the Unit notes.

RTP: (p ∨ q) ∧ ￢p → q
First consider:
p ∨ q Premise 1
≡ q ∨ p Commutativity
≡ ￢(￢ q) ∨ p Double negation
≡ ￢q → p Implication
￢p Premise 2

RTP: (p ∨ q) ∧ ￢p → q
p ∨ q Premise 1
￢p Premise 2
So we have, (￢q → p) ∧ ￢p
Recall: [(p → q) ∧ ￢ q] → ￢ p so applying this
inference rule, we have [(￢q → p) ∧ ￢p] → ￢￢q

RTP: (p ∨ q) ∧ ￢p → q
And putting it all together, we have:
p ∨ q Premise 1
≡ q ∨ p Commutativity
≡ ￢(￢ q) ∨ p Double negation
￢p Premise 2
￢(￢ q) Modus tollens
Conclusion: q Double negation
Hence, (p ∨ q) ∧ ￢p → q

Direct Proof
• A proof with no special assumptions is called a direct proof.
• Basic Steps in Direct Proof
• Deconstruct Axioms: Take the hypothesis and turn it into a usable
form. Usually this amounts to just applying the definition. EG: k =
1(mod 3) really means 3|(k - 1) which actually means n k - 1 = 3n
• Mathematical Insights: Use your human intellect and get at “real
reason” behind theorem. For instance, looking at what we’re
trying to prove, we see that we’d really like to understand k 3. So
let’s take the cube of k! From here, we’ll have to use some algebra
to get the formula into a form usable by the final step:
• Reconstruct Conclusion: This is the reverse of step 1. At the end
of step 2 we should have a simple form that could be derived by
applying the definition of the conclusion.

Using symbolic derivation, prove that
q ∧ ￢(p → q) is a contradiction.
q ∧ ￢(p → q) ≡ q ∧ ￢ (￢p ∨ q) Conditional equivalence
≡ q ∧ (￢￢p ∧ ￢ q) …

Using symbolic derivation, prove that
q ∧ ￢(p → q) is a contradiction.
q ∧ ￢(p → q) ≡ q ∧ ￢ (￢p ∨ q) Conditional equivalence
≡ q ∧ (￢￢p ∧ ￢ q) De Morgan’s law
≡ q ∧ (￢ q ∧ ￢￢ p) Commutative
≡ (q ∧ ￢ q) ∧ ￢￢ p Associative
≡ F ∧ ￢￢ p) Negation
≡ F Domination
This is a direct proof.

Proof by Cases
Proof by exhaustion, also known as proof by cases, proof by
case analysis, complete induction or the brute force method,
is a method of mathematical proof in which the statement to
be proved is split into a finite number of cases or sets of
equivalent cases, and where each type of case is checked to see
if the proposition in question holds.
This is a method of direct proof.A proof by exhaustion typically
contains two stages:
A proof that the set of cases is exhaustive; i.e., that each
instance of the statement to be proved matches the conditions
of (at least) one of the cases.
A proof of each of the cases.

To prove: the sum of any two squared integers leaves
a remainder of either 0, 1 or 2 when divided by 4.
• Here, we have three cases to consider:
• Both a and b even
• One of a, b even
• Both a and b odd
• If the integers are odd, let them be 2n + 1 and 2m + 1
where n and m are integers.
• If they are even, let them be 2n and 2m where n and m
are integers.

Consider the case of both integers even
• If they are even, let them be 2n and 2m
• Their squares are 4n2 and 4m2 and the sum
is 4n2 + 4m2.
• When divided by 4 this gives us a
remainder of 0.

Consider the case of both integers odd
• If they are odd, let them be 2n + 1 and 2m
+ 1 where n and m are integers.
• Their squares are 4n2 + 4n + 1 and 4m2 +
4m + 1 and the sum is 4n2 + 4n+ 4m2 + 2
remainder of 2.

Consider the case of one integer even and the other odd
• Let them be 2n (even) and 2m + 1 (odd)
• Their squares are 4n2 and 4m2 + 4m + 1 and
the sum is 4n2 + 4n+ 4m2 + 1
remainder of 1.

Indirect Proof
This is basically proof using the contrapositive.
Method: For any k, assume ￢Q(k) and derive ￢P(k)
Then, by the contrapositive logical equivalence:
P(k) → Q(k) ≡ ￢ Q(k) → ￢P(k)
Offer an example of an indirect proof.

Show that: if n is an integer and n3 + 5 is odd, then n is even.
Let the propositions be:
• p: n3 + 5 is odd
• q: n is even
So we want to show that p → q
To prove that we shall use the contrapositive? What
do we have to show in this case?

The propositions are: p: n3 + 5 is odd, and q: n is even
So we want to show that p → q
The contrapositive: ￢q → ￢p.
ie If n is odd , then n3 + 5 is even.
So let n = 2k + 1 for some integer k
⇒ n3 + 5 = (2k + 1)3 + 5
= 8k3 + 3.4k2 + 3.4k + 1 + 5
= 8k3 + 12k2 + 12k + 6
= 2(4k3 + 6k2 + 6k + 3) which is even.
We have shown that n odd → n3 + 5 is even and so if
n is an integer and n3 + 5 is odd, then n is even.
Show that: if n is an integer and n3 + 5 is odd, then n is even.

Proof by Contradiction
• A proof method by which an assumption is made and
the argument that follows reaches a contradiction.
This means that the original assumption is wrong.
• To show that some sentence is true, we assume that it
is false (we assume the negation of that sentence) and
then show any contradiction.
• If a contradiction follows, something has gone wrong;
and if we follow our rules of logic then the only thing
that can have gone wrong was our assumption of the
negation of our conclusion. So, we must have been
wrong to assume it is false, so it must be true.

The set of primes is infinite.
• Assume that the set of primes is finite and let
them be p1, p2, p3 ,…, pn.
• Now form the number p1p2p3…pn + 1.This is
clearly not divisible by any of the previous
primes and hence is prime.
• We have found a prime which is not in the set
{p1, p2, p3 ,…, pn} and this is a contradiction.
• Hence, the set of primes is infinite.

Principle of Mathematical Induction
Find base case P(1)
Assume P(k) and prove that P(k) → P(k + 1)
Then we have ∀k P(k)

n ∈ Z, 6 | n3 + 5n (i.e. that 6 divides n3 + 5n )
P (1): Clearly with n = 1, 6 | 13 + 5 TRUE
Assume P(k) then 6 | k3 + 5k for some k. Now we must
show P(k) → P (k + 1)
Substituting k + 1 for k, we have (k + 1)3 + 5(k + 1)
= k3 + 3k2 + 3k + 1 + 5k + 5
= k3 + 5k + 3k2 + 3k + 6
= k3 – k + 6k + 6 + 3k(k + 1)
= k(k2 – 1) + 6k + 6 + 3k(k + 1)
= (k – 1)k(k + 1) + 6k + 6 + 3k(k + 1)
Now any three consecutive integers must contain one
which is a multiple of 2 and one which is a multiple of 3.
Thus, 6 | (k – 1)k(k + 1). Also, observe that 3k2 + 3k = 3k (k +
1) and that k(k + 1) is an even number so 6 | 3k (k + 1).
We have shown that P(k) → P(k+1) and hence we have
P(n) for all n. ■

Arguments and methods of proof

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Arguments and methods of proof

Similar to Arguments and methods of proof (20)

More from Robert Geofroy

More from Robert Geofroy (11)

Recently uploaded

Recently uploaded (20)

Arguments and methods of proof