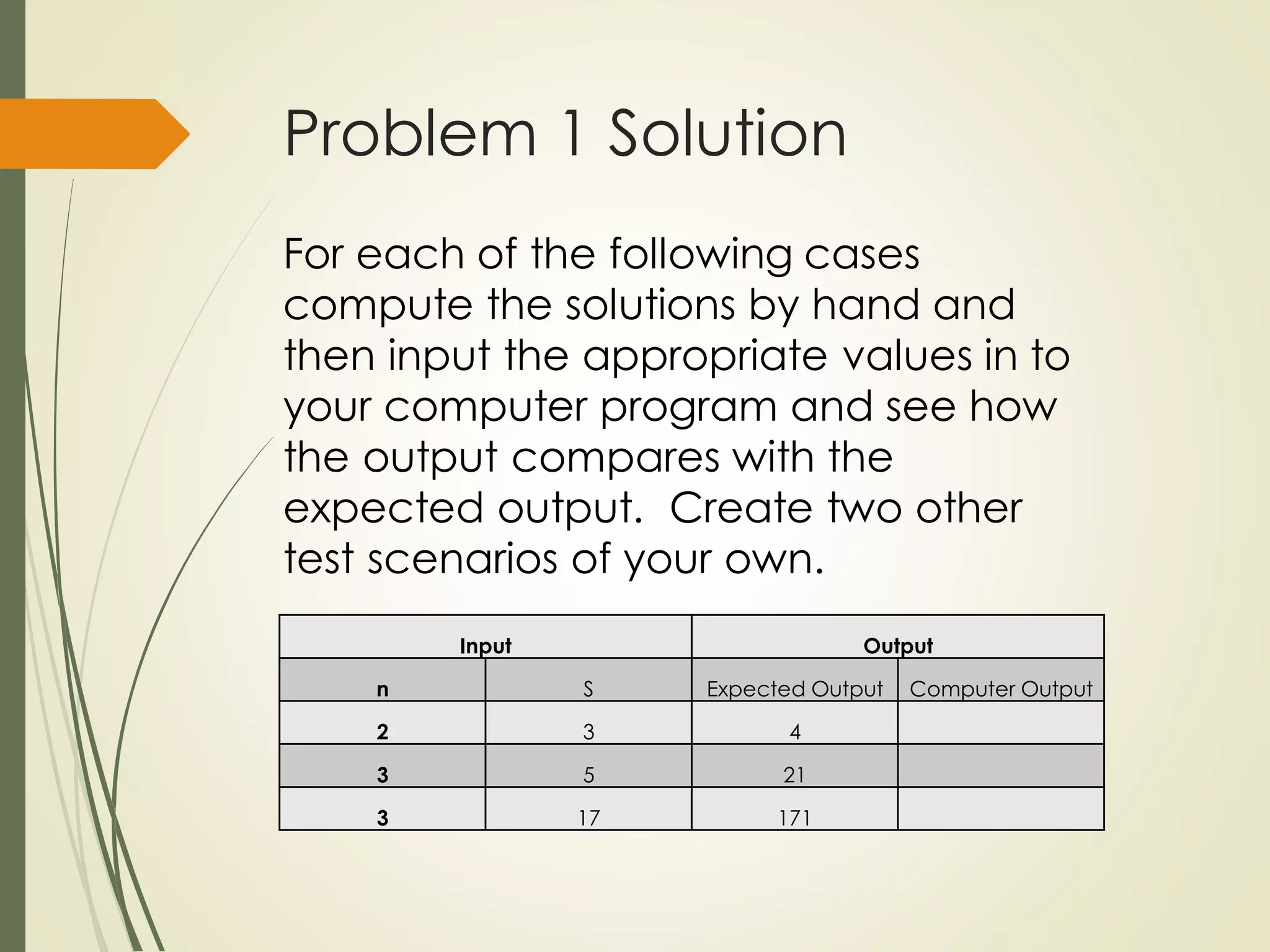
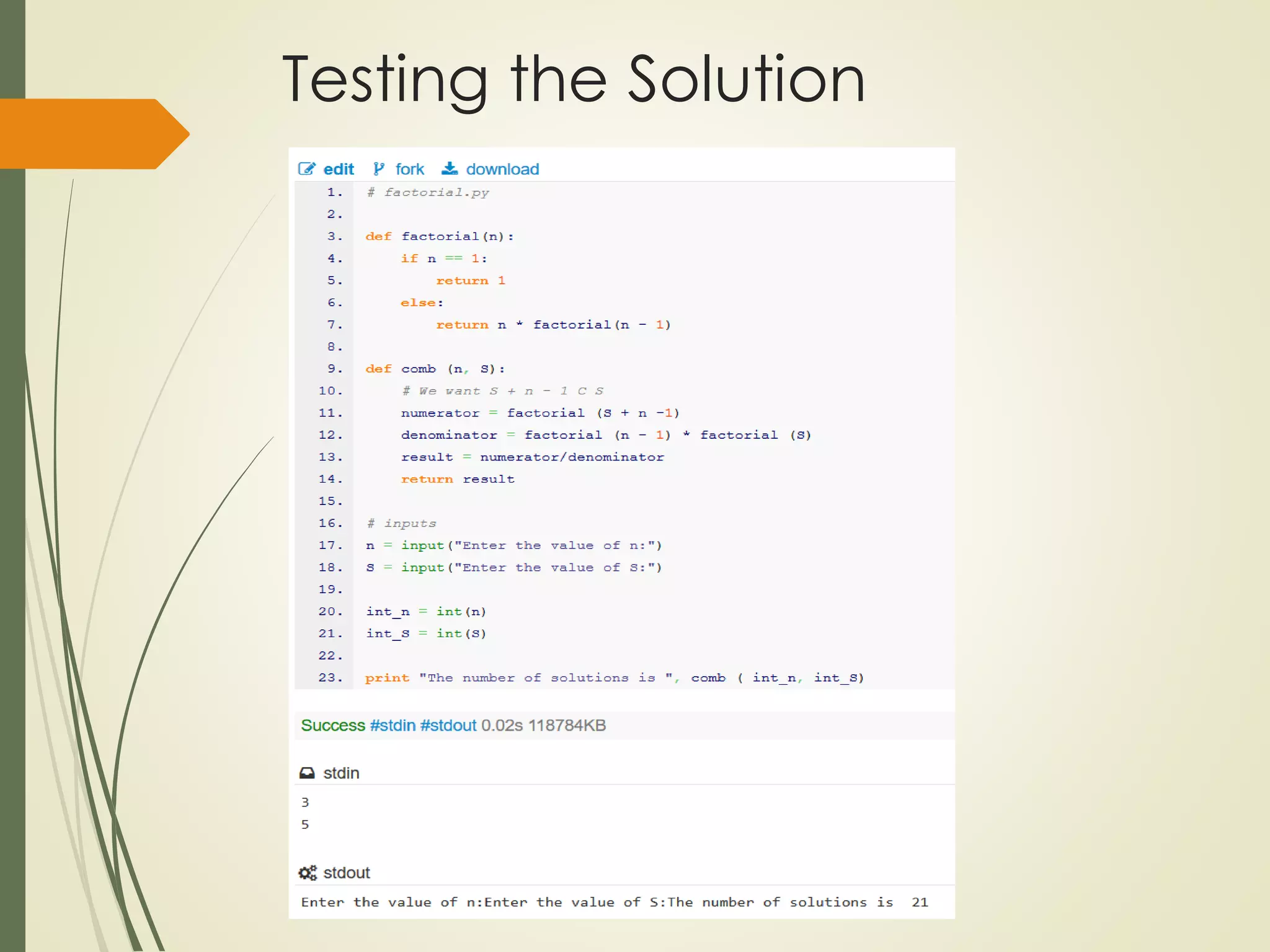
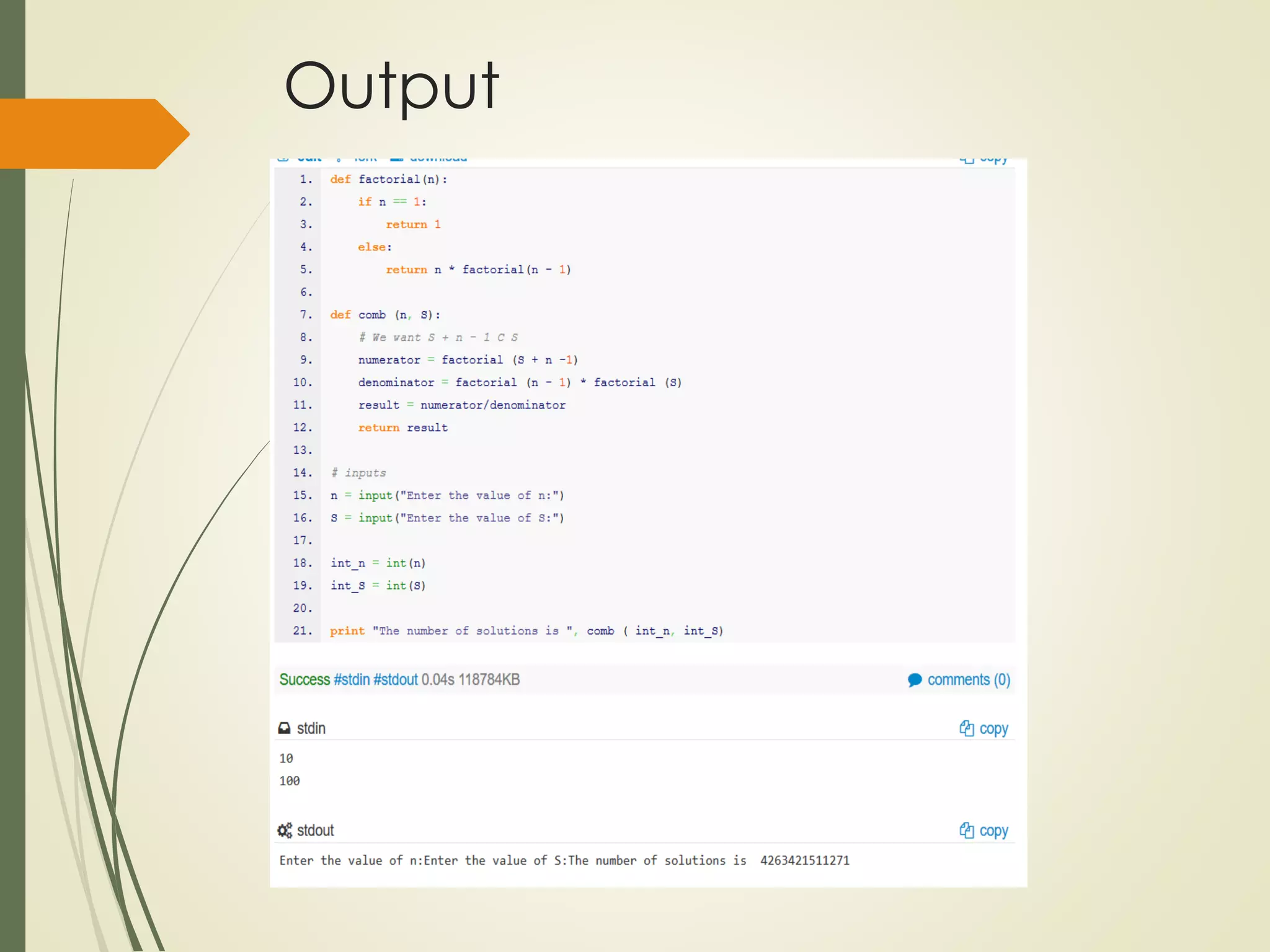
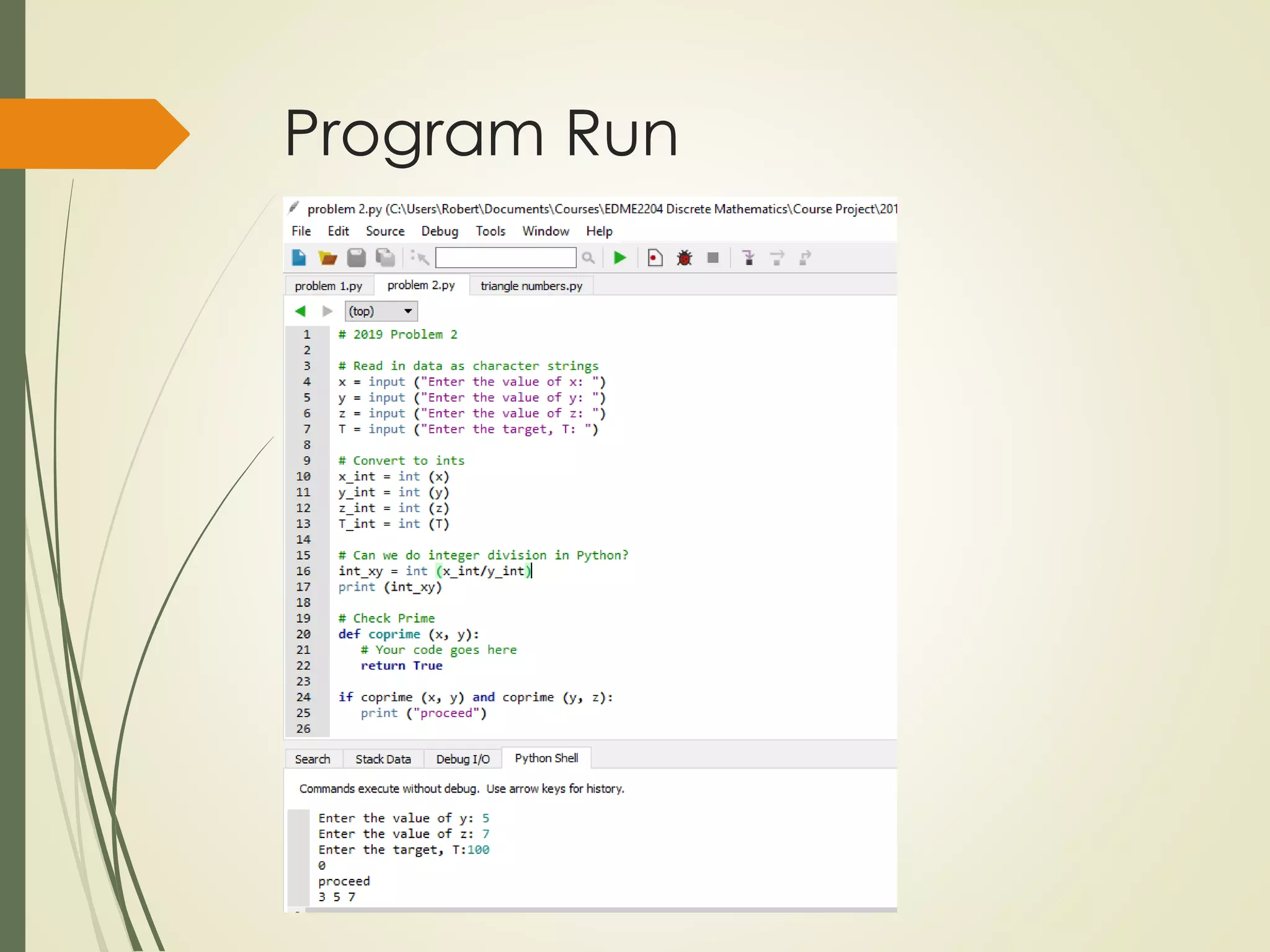
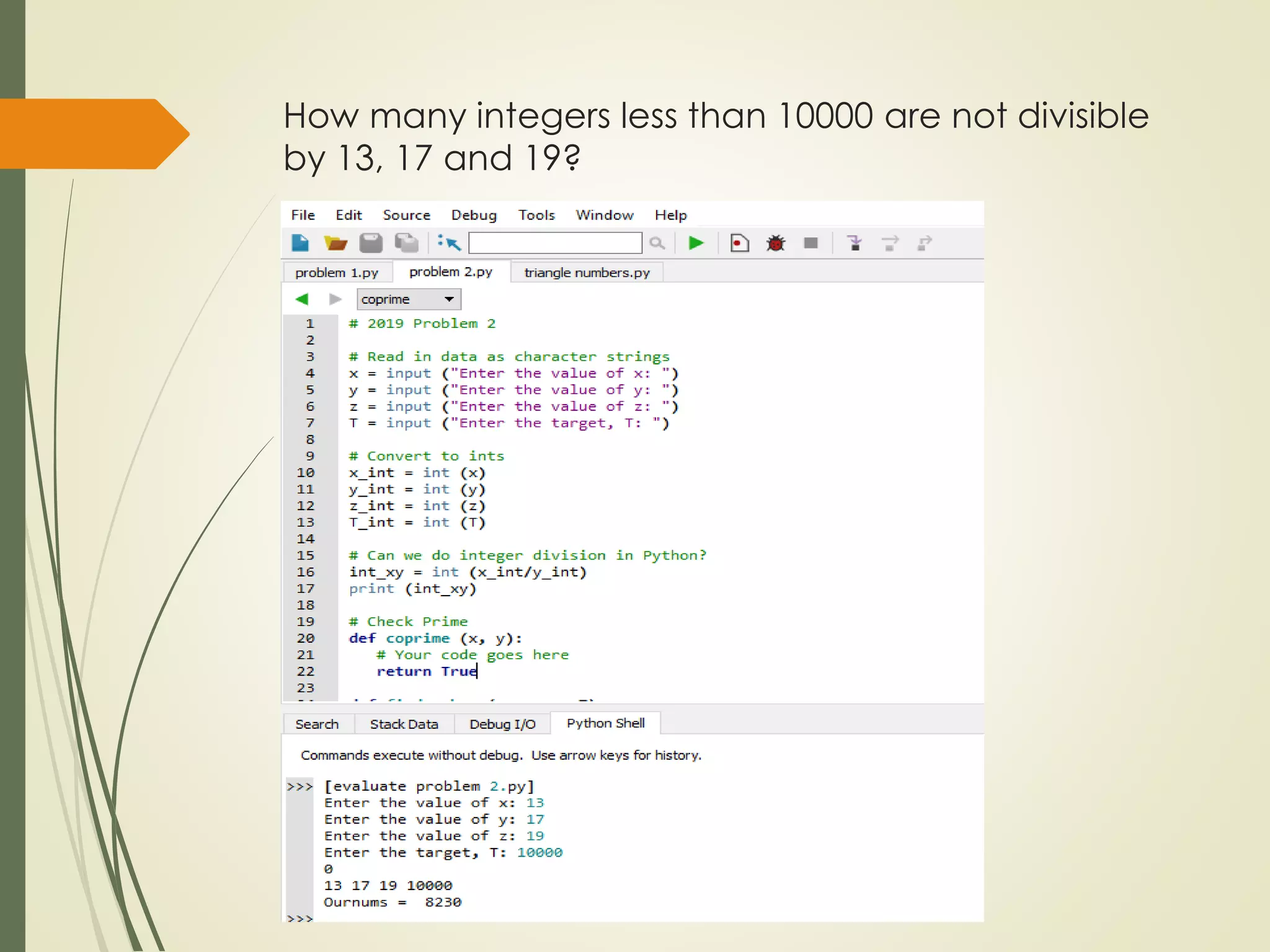
The course project involves solving two counting problems using a computer program. Problem 1 asks students to write a program to count the number of positive integer solutions to an equation with multiple variables summing to a given total. Problem 2 uses the principle of inclusion-exclusion to count the number of integers below a threshold that are not divisible by three given numbers. Students are provided templates to guide their programming solutions and are asked to test their programs on sample cases.

1. Course Project
Solutions
Discrete Mathematics 2019

2. Requirements
The Course project consists of two counting problems. In
the past, we have had counting problem involving
primes, triangle numbers and paths. Invariably, you would
have to use a computer program to find the solution.
There is no requirement for any particular programming
language and the choice is up to you.
I have tried to find some interesting and relevant
counting problems which can be solved using basic
computer knowledge. Have a look at the past questions
with some solution notes. That will help to give you an
idea of what the expectations are. You will however
need to put on your thinking cap and come up with a
suitable solution and test the solution using simpler
problems and apply it to the case you are asked to solve.

3. Requirements
For each problem, you will provide:
 Statement of Problem
 Solution
 Algorithms/Pseudocode/Dry run
 Code/Testing including screen prints of relevant output.
 Result
 Conclusion
 References
 Appendix: With code in a format which I can cut and
paste

4. Problem 1
How many positive integer solutions (including the
solutions in which xn= 0) are there to the equation
x1 + x2 + x3 + … + xn = S?
For instance, if we just have x1 + x2 = 3 then n = 2
and S = 3 and we could have x1 = 1 and x2 = 2, or x1
= 2 and x2 = 1 but we also have x1 = 0 and x2 = 3
and x1 = 3 and x2 = 0. So, in this case, there are four
solutions.
Write a computer program which accepts an
integer n, the number of x’s, and S, a value of the
sum, and computes the number of positive integer
solutions.
How many solutions are there when n = 10 and S =
100? Does your result seem reasonable? Comment.

5. Problem 1 Solution
# Problem 1: Number of
Combinations
# Programmer: Robert Geofroy
# Date: May 2019
# factorial.py
def factorial(n):
<< your code here>>
#Combinations
def comb (n, S):
<<Your code here>>
You are provided with this program template:
# Inputs
n = input ("Enter the value of n: ")
S = input ("Enter the value of S: ")
int_n = int(n)
int_S = int(S)
print ("The number of solutions is ",
comb ( int_n, int_S))

6. Testing
Input Output
n S Expected Output Algorithm Output
2 3 4
3 5
3 17 171
We are given a little help with the
following table for testing some cases…
We have to ensure that whatever
algorithm we devise, outputs the values
we calculated manually. This is the dry
run.

7. Problem 1 Solution
Input Output
n S Expected Output Computer Output
2 3 4
3 5 21
3 17 171
For each of the following cases
compute the solutions by hand and
then input the appropriate values in to
your computer program and see how
the output compares with the
expected output. Create two other
test scenarios of your own.

8. Problem 1 Solution
Take, x1 + x2 = 3. In this case we have x1 = 1 and x2 = 2 or x1 =
2 and x2 = 1 and x1 = 0 and x2 =3 or x1 = 3 and x2 = 0 so we
have 4 cases. The expected output is 4.
Recall the formula: n + r – 1C r = (n + r -1)!/r!(n – 1)!
Worked by hand:
With n = 2 and S = 3, we have solutions: 03 12 21 30
Check: n + S – 1 C S = 2 + 3 - 1 C 3 = 4!/3!1! = 4
With n = 4 and S = 5, we have solutions: 005 050 500 014 041
023 032 104 410 401 140 113 131 122 203 302 320 230 311 ...
With n = 3, S = 17, the number of solutions is 3 + 17 – 1 C 17 =
19C17 = 19!/17!2! = 19.9 = 171
Use your program to determine the number of solutions when
n =10 and S = 100.
Mathematical Justification

9. Python Code
# factorial.py
def factorial(n):
if n == 1:
return 1
else:
return n * factorial (n - 1)
#Combinations
def comb (n, S):
# We want S + n - 1 C S
numerator = factorial (S + n -1)
denominator = factorial (n - 1) * factorial (S)
result = numerator/denominator
return result
n = input ("Enter the value of n: ")
S = input ("Enter the value of S: ")

10. Testing the Solution

11. Problem 1 Testing the Solution
Input Output
n S Expected Output Computer Output
2 3 4 4
3 5 21 21
3 17 171 171
We test each of the scenarios
previously checked in the dry run and
compare with the computer output…

12. Case in Question
 The case in question is how many solutions are there
for n = 10 and S = 100. This is far more than we can
count manually so assuming that our program is
working, we can obtain the solution using these inputs.

13. Output

14. Output
 In the case of n = 10 and S = 100, we
have 4263421511271 solutions.

15. Conclusion
Given that there was clear grounds
mathematically for the solution design and
that the algorithm was dry run and given
that the program was tested using the test
cases for which the results were know, it is
safe to say that the output is reasonable
and correct. With these large numbers
one concern would be overflow but this
did not occur in this instance.

16. Problem 2
How many integers less than or equal to one thousand
are not divisible by either 5, 7 or 11? State any principle
which you use to arrive at your conclusion. What would
happen if we substituted 2, 4 and 5 for the three numbers
with T = 10? How would your solution differ? What would
be the count in that case?
Write a program which takes three integers x, y and z
prime to each other and a target, T and computes the
number of integers less than or equal to T that are not
divisible by either x, y or z. How many integers less than
10000 are not divisible by 13, 17 and 19?
Note that your program should test if x, y and z are prime
to each other as a condition for proceeding with the
calculation.
Prove any counting principles you use or employ in this
solution.

17. Problem 2 Solution
This solution uses the principle of inclusion-exclusion.
We are lucky that 5, 7 and 11 are primes. If they
weren’t then we would have a more difficult
problem. When we run our solution algorithm on
the integers 2, 4 and 5 with T = 10 we see that the
set intersection robs us of a clean solution.
Mathematical Justification

18. To Show:
|A∪B∪C|=|A|+|B|+|C|−|A∩B|−|B∩C|−|A∩C|+|A∩B∩C|
|A∪B∪C|=|A|+|B−A|+|C−B−A|
|A∩B|+|B−A|=|B|
|C−A|+|A∩C|=|C|
|C−B|+|+|B∩C|=|C|
|C−B−A|+|C|=|C−A|+|C−B|+|A∩B∩C|
summing the previous five equations gives
|A∪B∪C|=|A|+|B|+|C|−|A∩B|−|B∩C|−|A∩C|+|A∩B∩C|

19. Algorithm
Let Aj be the set of numbers between 1 and 1000 divisible by j.
We want to find the value of 1000 - |A5 Ս A7 Ս A11|. By the
Principle of Inclusion – Exclusion, we have:
|A5 Ս A7 Ս A11| = |A5| + |A7| + |A11| - |A5 ∩ A7| - |A5 ∩ A11| -
|A7 ∩ A11| + |A5 ∩A7 ∩ A11|
We have that |A5| = 200.
How did we arrive at that? 1000/5 = 200.
Also, |A7| = 1000/7 = 142 r 6 but the remainder does not count.
So |A7| = 142 and |A11| = 90.
|A5 ∩ A7| counts the number of numbers divisible by 5 and 7.
Since 5 and 7 are primes, we have |A5 ∩ A7| = |A35| = 28.
Similarly, - |A5 ∩ A11| = |A55| = 18 and |A7 ∩ A11| = |A77| = 12.
Finally, |A5 ∩A7 ∩ A11| = |A385| = 2.
Hence, |A5 U A7 U A11| = |A5| + |A7| + |A11| - |A5 ∩ A7| - |A5
∩ A11| - |A7 ∩ A11| + |A5 ∩A7 ∩ A11|
= 200 + 142 + 90 – 28 – 18 – 12 + 2 = 376 and we have 1000 – 376 =
624 numbers between 1 and 1000 are not divisible by 5, 7, 11.

20. Algorithm
In the case of 2, 4 and 5 with T = 10 the difference would be:
 We want to find the value of 10 - |A2 Ս A4 Ս A5|. By the
inclusion – Exclusion principle, we have:
 |A2 Ս A4 Ս A5| = |A2| + |A4| + |A5| - |A2 ∩ A4| - |A2 ∩
A5| - |A4 ∩ A5| + |A2 ∩A4 ∩ A5|
 We have A2 = {2, 4, 6, 8, 10} Thus, |A2| = 5; A4 = {4, 8}, so
|A4| = 2 and A5 = {5, 10} so |A5| = 2. A2 ∩ A5 = {10} Thus,
|A2 ∩ A5| =1. Since 2 and 5 are primes, they are also
coprime, and we have |A2 ∩ A5| = |A10| = 1. Similarly,
|A4 ∩ A5| = |A20| = 0. But now, A2 ∩ A4 = {4, 8} so |A2 ∩
A4| = |A4| = 2. Finally, |A2 ∩A4 ∩ A5| = 0.
 Hence, |A2 Ս A4 Ս A5| = |A2| + |A4| + |A5| - |A2 ∩ A4| -
|A2 ∩ A5| - |A4 ∩ A5| + |A2 ∩A4 ∩ A5|
 = 5 + 2 + 2 – 1 – 2 – 0 + 0 = 6 and we have 10 – 6 = 4
numbers between 1 and 10 are not divisible by 2, 4, 5.
These numbers are 1, 3, 7, 9.

21. Computer Program
We can also do this in Python. Python will pose
some interesting challenges to you, but the coding
is simple. We will need to be able to
 Input the three variables, x, y, z and the target T
 Convert the character string input into ints
 Code the algorithm

22. Problem 2 Solution
# 2019 Problem 2
# Programmer: Robert Geofroy
# Date: April 2019
# Read in data as character strings
x = input ("Enter the value of x: ")
<< Your code here>>
# Convert to ints
x_int = int (x)
<< Your code here>>
# Can we do integer division in Python?
int_xy = int (x_int/y_int)
print (int_xy)
# Define GCD
def gcd(a, b):
<<Your code here>>
# Define GCD
def gcd(a, b):
<<Your code here>>
# Define coprime function
def coprime(a, b):
<< Your code here>>
def findnumber (x, y, z, T):
<< your code here>>
return total
if coprime (x_int, y_int) and coprime
(y_int, z_int) and coprime (x_int, z_int):
<<Your code here>>)

23. Problem 2 Solution
# 2019 Problem 2
# Programmer: Robert Geofroy
# Date: April 2019
# Read in data as character strings
x = input ("Enter the value of x: ")
y = input ("Enter the value of y: ")
z = input ("Enter the value of z: ")
T = input ("Enter the target, T: ")
# Convert to ints
x_int = int (x)
y_int = int (y)
z_int = int (z)
T_int = int (T)
# Can we do integer division in Python?
int_xy = int (x_int/y_int)
print (int_xy)
# Define GCD
def gcd(a, b):
while b != 0:
a, b = b, a % b
return a
# Define coprime function
def coprime(a, b):
return gcd(a, b) == 1
def findnumber (x, y, z, T):
# your code here
num_1 = int (T/x) + int (T/y) + int (T/z)
num_2 = int (T/(x*y)) + int (T/(y*z)) + int (T/(x*z))
num_3 = int (T/(x*y*z))
total = num_1 - num_2 + num_3
return total
if coprime (x_int, y_int) and coprime (y_int, z_int) and
coprime (x_int, z_int):
print (x, y, z, T)
nums = findnumber (x_int, y_int, z_int, T_int)
print ("Cases = ", T_int - nums)
else:
print ("Numbers are not coprime.")

24. Program Run

25. Testing
x y z T Expected Output Computer Output
2 3 5 10 2
2 4 5 10 Not coprime
…add more rows if
necessary
In the case of x = 2, y = 3 and z = 5 with T = 10, there
are 2 numbers which are not divisible by either 2, 3,
or 5. These are: 1 and 7.

26. Testing
x y z T Expected Output Computer Output
2 3 5 10 2
2 4 5 10 Not coprime
…add more rows if
necessary
If we put x = 2, y = 4 and z = 5 with T = 10 we should
get an error message saying the numbers are not
coprime.

27. Testing
x y z T Expected Output Computer Output
2 3 5 10 2
2 4 5 10 Not coprime
5 7 11 624 624
5 15 11 Not coprime
The complete set of test cases is shown below:

28. How many integers less than 10000 are not divisible
by 13, 17 and 19?

29. Program Run
For x = 13, y = 17 and z = 19 with target = 10000 the
program gives 8230 as the answer.

30. Conclusion
The code has been tested using cases for which the
result can be computed mentally and by hand and
from all appearances it is working as expected. It
also deals with the case where the numbers are not
coprime as per the requirements of the question.
From all appearances, the program is working as
expected.