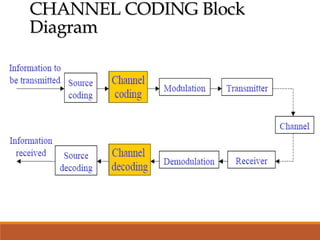
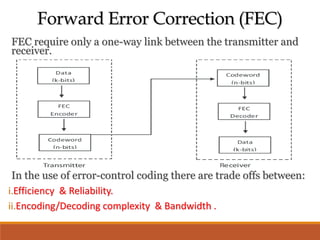
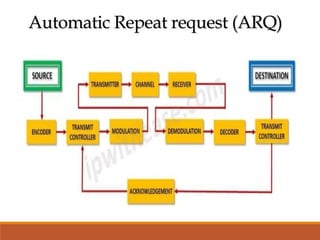
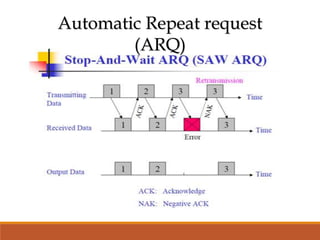
Channel coding is used in digital communication systems to provide error control and allow reliable transmission of information over noisy channels. The two main methods of error control coding are forward error correction (FEC) and automatic repeat request (ARQ). FEC encodes redundant data into each message to allow the receiver to correct errors without requesting retransmissions, while ARQ relies on the receiver to request retransmission of corrupted data. Common types of FEC codes include block codes, cyclic codes, and convolutional codes, with each code characterized by parameters like coding rate and minimum distance that determine its error detection and correction capabilities.