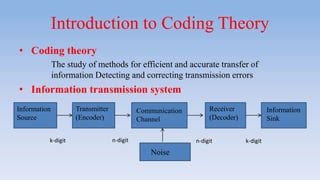
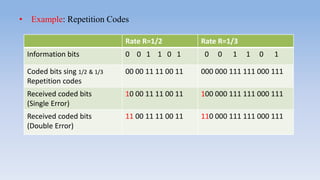
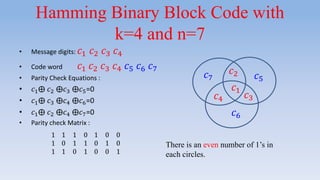
This document provides an introduction to error correcting codes. It discusses key concepts such as channel capacity, error detection and correction, information rate, weight and distance, maximum likelihood decoding, and linear codes. Error correcting codes add redundant bits to messages to facilitate detecting and correcting errors that may occur during transmission or storage. Linear codes allow for simpler encoding and decoding procedures compared to non-linear codes. The generator and parity check matrices are important for encoding and decoding messages using linear codes.

1. INTRODUCTION TO ERROR
CORRECTING CODES

2. Outline
 Introduction
 Basic assumptions
 Correcting and detecting error patterns
 Information Rate
 The effects of error correction and detection
 Weight and distance
 Reliability of MLD
 Error-detecting codes
 Error-correcting codes

3.  In his landmark paper in 1948, “ A Mathematical Theory of Communication”, in
Bell System Technical Journal, Shannon introduced the concept of channel
capacity.
 Shannon in his celebrated noisy channel coding theorem proved the existence of
channel coding schemes that can achieve coding schemes that can achieve an
arbitrarily low error probability as long as the information can be transmitted across
the channel at a ‘rate’ less than the channel capacity C.
 A channel code is designed by properly adding redundant bits(parity bits) to the
source bits. These redundant bits facilitate the detection and correction of
transmission (storage) errors.
 In digital storage systems, channel coding is used to control errors caused by
storage medium defects, dust particles, radiation.
Introduction

4. All Communications involves three basic steps
• Encoding a message at its source
• Transmitting that message through a communication
medium.
• Decoding the message at its destination.
• The transmission medium in communication is
known as channel.

5. Binary symmetric channel: Assumptions
1. Data (Information) is binary
2. Each bit has equal probability of getting corrupted
3. The error in one bit has no effect in the error in other bit
0
11
0
1-P
1-P
P
P

6. Introduction to Coding Theory
• Coding theory
The study of methods for efficient and accurate transfer of
information Detecting and correcting transmission errors
• Information transmission system
Information
Source
Transmitter
(Encoder)
Communication
Channel
Receiver
(Decoder)
Information
Sink
Noise
k-digit k-digitn-digitn-digit

7. Basic assumptions
Definitions
 Digit : 0 or 1(binary digit)
 Word : a sequence of digits
 Example: 0110101
 Binary code : a set of words
 Example : 1. {00,01,10,11} 2.{0,01,000}
 Block code : a code having all its words of the same length
 Example :{00,10,01,11}
 Code words : words belonging to a given code
 𝐶 : Size of a code C(# code words in C)

8. The effects of error correction
and error detection
If there is no error detection and correction??
Let C={0,1}11
={00000000000,…,11111111111}
Error Probability p=10−8
Transmission rate= 107
digits/sec
Then Pr(a word is transmitted incorrectly)= 0.1 wrong words/sec
1 wrong word /10 sec
6 wrong words /min
360 wrong words / hr
8640 wrong words / day

9. Some basic algebra
• Field 𝐹2 ={0,1}
Addition : 0+0=0, 0+1=1, 1+0=1, 1+1=0
Multiplication : 0.0=0, 1.0=0, 0.1=0, 1.1=1
• 𝐹2
𝑛
: the set of all binary words of length n (It is a vector space over 𝐹2)
Addition : 01101+11001=10100
Scalar multiplication : 0.u= , 1.u=u where is the Zero word0n
0n

10. Weight and distance
• Hamming weight: wt(v)
the number of times the digit 1 occurs in v
Example : wt(110101)=4, wt(000000)=0
• Hamming distance : d( v, w)
the number of positions in which v and w disagree
Example : d(01011,00111)=2, d(10110,10110)=0

11. Information rate
• Definition: information rate of code C
is defined as R =
1
𝑛
𝑙𝑜𝑔2 𝐶
where n is the length of C
Examples
𝐶1 = {00,01,10,11} 𝐶2 = {000,111} 𝐶3 = {001,010,100,111}
𝑅1 =
1
2
𝑙𝑜𝑔24 = 1 𝑅2 =
1
3
𝑅3 =
2
3

12. Maximum Likelihood Decoding(MLD)
• CMLD : Complete Maximum Likelihood Decoding
If only word v in C closer to w, decode it to v
If several words closest to w, decode it to V
• IMLD : Incomplete Maximum Likelihood Decoding
If only one word v in C closer to w, decode it to v
If several words closest to w, ask for retransmission
k-message bits (n-k) bits
n-bits
Code word v
channel
w = v + u
Error pattern u
CMLD
IMLD
Decode w

13. • Example: Repetition Codes
Rate R=1/2 Rate R=1/3
Information bits 0 0 1 1 0 1 0 0 1 1 0 1
Coded bits sing 1/2 & 1/3
Repetition codes
00 00 11 11 00 11 000 000 111 111 000 111
Received coded bits
(Single Error)
10 00 11 11 00 11 100 000 111 111 000 111
Received coded bits
(Double Error)
11 00 11 11 00 11 110 000 111 111 000 111

14. Error detecting codes
• The minimum distance (simply, distance) of the code C
i.e., the smallest of d( v, w) in C
• Theorem : A code C of distance d will at least detect all non zero error
patterns of weight less than or equal to d-1. Moreover, there is at least one
error pattern of weight d which C will not detect.
• t-error detecting code
It detects all error patterns of weight at most t and does not detect at
least one error pattern of weight t+1
• A code with distance d is a (d-1)- error detecting code

15. Error-correcting codes
• Theorem : A code of distance d will correct all error patterns of weight less than or
equal to (d−1)/2 . Moreover, there is at least one error pattern of weight
1+ (d−1)/2 which C will not correct.
• t error-correcting code
It corrects all error patterns of weight at most t and does not correct at least
one error pattern of weight t+1.
• A code of distance d is a (d−1)/2 error-correcting code.
v
u
w+ For all v in C, if it is
closer to v than any other
word in C, a code C can
correct u.

16. Hamming Binary Block Code with
k=4 and n=7
o In general, a block code with k information digits and block
length n is called ( n, k)-code
o Thus, this example is called an ( 7, 4)-code
o This is a very special example where we use pictures to
explain the code other codes are NOT explainable in this way.
o All that we need to know is modulo 2 addition,
0+0=0, 1+0=1, 0+1=1, 1+1=0.

17. Hamming Binary Block Code with
k=4 and n=7
• Message digits: 𝑐1 𝑐2 𝑐3 𝑐4
• Code word 𝑐1 𝑐2 𝑐3 𝑐4 𝑐5 𝑐6 𝑐7
• Parity Check Equations :
• 𝑐1⨁ 𝑐2 ⨁𝑐3 ⨁𝑐5=0
• 𝑐1⨁ 𝑐3 ⨁𝑐4 ⨁𝑐6=0
• 𝑐1⨁ 𝑐2 ⨁𝑐4 ⨁𝑐7=0
• Parity check Matrix :
1
1
1
1 1 0
0 1 1
1 0 1
1 0 0
0 1 0
0 0 1
𝑐7
𝑐1
𝑐2
𝑐3
𝑐5
𝑐4
𝑐6
There is an even number of 1’s in
each circles.

18. Hamming (7,4) Code : Encoding
• Message : ( 𝑐1 𝑐2 𝑐3 𝑐4 ) = ( 0 1 1 0 )
• Resultant code word : 0110011
𝑐6
𝑐7
0
1
1
𝑐5
0

19. Hamming (7,4) Code : Decoding
• Transmitted code word : 0110011
• Example
1. Received block with one error in a message bit 0100011
By counting 1’s in each circle we find :
There is an error in right circle.
There is an error in bottom circle.
There is no error in left circle.
Therefore the error is in the third digit!
𝑐6=1
𝑐7=1
0
1
0
𝑐5 = 0
0

20. Hamming (7,4) Code : Decoding
• Transmitted code word : 0110011
• Example
2. Received block with one error in a message bit 0110001
By counting 1’s in each circle we find :
There is no error in right circle.
There is an error in bottom circle.
There is no error in left circle.
Therefore the error is in the six digit!
𝑐6=0
𝑐7=1
0
1
1
𝑐5 = 0
0

21. Hamming (7,4) Code : Decoding
• Transmitted code word : 0110011
• Example
3. Received block with one error in a message bit 1110001
By counting 1’s in each circle we find :
There is an error in right circle.
There is no error in bottom circle.
There is an error in left circle.
Therefore the error is in the second digit!
WRONG!!!
𝑐6=0
𝑐7=1
1
1
1
𝑐5 = 0
0

22. Linear codes

23. Outline
 Linear codes
 Generator Matrix
 Block Codes in Systematic Form
 Block Codes : Encoding
 Parity-check Matrix
 Syndrome and error detection
 Properties of syndrome
 Block Codes : Syndrome Decoding
 Applications

24. Linear codes
• A code C is called a linear code if v+w is a word in C where v and w are in C
• C must contain the zero word
• C is a linear code(group code) iff C is a(subspace) subgroup of 𝐾 𝑛
• We will the knowledge of subspace to dramatically improve our techniques for
encoding and decoding
• The minimum distance of a linear code is equal to the minimum weight of any
nonzero code word.
Advantage :
• simpler procedure for MLD
• Faster encoding and less storage space
• Error patterns are easily describable

25. • Example : S={0100,0011,1100} is a subspace.
0100+0011=0111, 0100+0011=1011
0100+1100=1000, 0011+1100=1111
C=<S>={0000,0100,0011,1100,0111,1000,1111,1011}
where <S> is Linear span of S
Hence C is linear code

26. Generator Matrix
• All code words can be obtained as linear combination of basis vectors
• The basis vectors can be designated as { 𝑔1, 𝑔2, 𝑔3,…, 𝑔 𝑘 }
• For a linear code, there exists a k by n generator matrix such that
𝐶1×𝑛 = 𝑚1×𝑘 *𝐺 𝑘×𝑛
Where C={ 𝑐1, 𝑐2, 𝑐3,…, 𝑐 𝑛} and m={ 𝑚1, 𝑚2, 𝑚3,…, 𝑚 𝑘}
𝐺 =
𝑔1
𝑔2
⋮
𝑔 𝑘
=
𝑔11 𝑔12 … 𝑔1𝑛
𝑔21 𝑔22 … 𝑔2𝑛
⋮
𝑔 𝑘1
⋮
𝑔 𝑘2
⋱
…
⋮
𝑔 𝑘𝑛

27. Block Codes in Systematic Form
• In this form, the code word consists of (n-k) parity check bits followed by k bits of
the message.
• The rate or efficiency for this code R = k/n.
• The structure of the code word in systematic form is :
𝐺 𝑘×𝑛= 𝐼 𝑘×𝑘 𝑃(𝑛−𝑘)×𝑛
Code C = m.G = [m mP]

28. Block Codes : Encoding
• Example : Let m=(𝑚1, 𝑚2, 𝑚3, 𝑚4) and c =(𝑐1, 𝑐2, 𝑐3, 𝑐4, 𝑐5, 𝑐6, 𝑐7)
c = m.G = (𝑚1, 𝑚2, 𝑚3, 𝑚4)
1 1 0 1 0 0 0
0 1 1 0 1 0 0
1 1 1 0 0 1 0
1 0 1 0 0 0 1
By matrix multiplication we obtain :
𝑐1= 𝑚1+𝑚3+𝑚4 , 𝑐2=𝑚1+𝑚2 + 𝑚3, 𝑐3=𝑚2+𝑚3+𝑚4, 𝑐4=𝑚1,
𝑐5=𝑚2, 𝑐6=𝑚3, 𝑐7=𝑚4.
The code word corresponding to the message (1110) is (0101110)

29. Parity Check Matrix
• When G is systematic, it is easy to determine the parity check matrix H as :
H=[𝐼(𝑛−𝑘)×(𝑛−𝑘) 𝑃 𝑇
(𝑛−𝑘)×𝑛]
• The parity check matrix H of a generator matrix is an (n-k)-by-n matrix satisfying:
𝐻(𝑛−𝑘)×𝑛 ∗ 𝐺 𝑇
𝑛×𝑘 = 0
• Then the code words should satisfy (n-k) parity check equations
𝑐1×𝑛 ∗ 𝐻 𝑇
𝑛×(𝑛−𝑘) = 𝑚1×𝑘 ∗ 𝐺 𝑘×𝑛* 𝐻 𝑇
𝑛×(𝑛−𝑘) = 0

30. Syndrome and error detection
• For a code word c, transmitted over a noisy channel, let r be the received
vector at the output of the channel with error e
𝑒𝑖=
1, 𝑖𝑓 𝑟 ≠ 𝑐
0, 𝑖𝑓 𝑟 = 𝑐
Syndrome of received vector r is given by:
s = r.𝐻 𝑇
= (𝑠1, 𝑠2, 𝑠3, … , 𝑠(𝑛−𝑘))

31. Properties of syndrome
• The syndrome depends only on the error pattern and not on
the transmitted word.
s = (c+e).𝐻 𝑇=c. 𝐻 𝑇 + e. 𝐻 𝑇=e. 𝐻 𝑇
• All the error pattern differ by at least a code word have the
same syndrome s.

32. Block Codes : Syndrome Decoding
• Example : Let C=(0101110) be the transmitted code and r=(0001110) be the
received vector.
s = r.𝐻 𝑇 = (𝑠1, 𝑠2, 𝑠3) = (𝑟1, 𝑟2, 𝑟3, 𝑟4, 𝑟5, 𝑟6, 𝑟7)
1 0 0
0 1 0
0 0 1
1 1 0
0 1 1
1 1 1
1 0 1

33. Block Codes : Syndrome Decoding
• Example : Let C=(0101110) be the transmitted code and r=(0001110) be the
received vector.
s = r.𝐻 𝑇
= (𝑠1, 𝑠2, 𝑠3)
The syndrome digits are 𝑠1= 𝑟1+𝑟4+𝑟6+𝑟7 = 0
𝑠2= 𝑟2+𝑟4+𝑟5+𝑟6 = 1
𝑠3= 𝑟3+𝑟5+𝑟6+𝑟7 = 0
The error vector, e =(𝑒1, 𝑒2, 𝑒3, 𝑒4, 𝑒5, 𝑒6, 𝑒7) = (0100000)
𝐶∗
= r + e = (0001110) + (0100000) = (0101110)
where 𝐶∗
is the actual transmitted code word.

34. Applications
• Communications:
Satellite and deep space communications
Digital audio and video transmissions
• Storage :
Computer memory(RAM)
single error correcting and double error detecting code

35. ADVANTAGES
• It is the easiest and simplest
technique to detect and correct
errors
• Error probability is reduced
DISADVANTAGES
• Transmission bandwidth requirement
is more
• Extra bits reduces bit rate of
transmitter and also reduces its
power

36. Cyclic codes

37. Cyclic codes
• Definition A code C is cyclic if
1. C is a linear code
2. any cyclic shift of a code word is also a code word.
i.e.,𝑎1, 𝑎2,…, 𝑎 𝑛 ∈ 𝐶 then also 𝑎 𝑛, 𝑎1,…, 𝑎 𝑛−1 ∈ 𝐶.
Example: code C={000, 101, 011, 110} is cyclic

38. Generator Polynomials
• Definition If for a cyclic code C it holds C=<𝑔(𝑥)>, then 𝑔 is called the
generator polynomial for the code C where 𝑔(𝑥) is a factor of 𝑥 𝑛 − 1.
• Theorem Suppose C is cyclic code of code words of length n with the
generator polynomial 𝑔(𝑥) =𝑔0 + 𝑔1 𝑥 + ⋯ + 𝑔 𝑟 𝑥 𝑟
Then dim(C)=n-r and a generator matrix G for C is
G=
𝑔0 𝑔1 𝑔2 … 𝑔 𝑟 0 0 0 … 0
0 𝑔0 𝑔1 𝑔2 … 𝑔 𝑟 0 0 … 0
0 0 𝑔0 𝑔1 𝑔2 … 𝑔 𝑟 0 … 0
⋮ ⋮ ⋱ ⋱ ⋱ ⋱ ⋱ ⋱ ⋱ ⋮
0 0 … 0 0 … … 𝑔0 … 𝑔 𝑟

39. Parity check matrices for cyclic codes
• Let C be a cyclic [ n, k]-code with the generator polynomial g(𝑥) (of degree n-k),
By the last theorem g(𝑥) is a factor of 𝑥 𝑛 − 1. Hence 𝑥 𝑛 − 1 =𝑔 𝑥 ℎ(𝑥) for some
h(𝑥) of degree K (where h(𝑥) is called the check polynomial of C)
• Theorem: Suppose C is a cyclic [ n, k]-code with the check polynomial
h(𝑥) =ℎ0 + ℎ1 𝑥 + ⋯ + ℎ 𝑘 𝑥 𝑘 then a parity-check matrix for C is
H=
ℎ 𝑘 ℎ 𝑘−1 ℎ 𝑘−2 … ℎ0 0 0 0 … 0
0 ℎ 𝑘 ℎ 𝑘−1 ℎ 𝑘−2 … ℎ0 0 0 … 0
0 0 ℎ 𝑘 ℎ 𝑘−1 ℎ 𝑘−2 … ℎ0 0 … 0
⋮ ⋮ ⋱ ⋱ ⋱ ⋱ ⋱ ⋱ ⋱ ⋮
0 0 … 0 0 … … ℎ 𝑘 … ℎ0

40. Basic Definitions of Posets
• P=([n], ≤ 𝑃) is a partial order (or Poset) on [n] where [n]={1,2,…,n} (or n-set)
• Given u=(𝑢1, … , 𝑢 𝑛)∈ 𝐹2
𝑛
, the support of u is the set supp(u)={i∈ [𝑛]:𝑢𝑖 ≠0}
• The P-distance of u and v is the cardinality 𝑑 𝑝 𝑢, 𝑣 = 𝑠𝑢𝑝𝑝(𝑢 − 𝑣)
• A poset code is a linear subspace C of the metric space (𝐹2
𝑛
, 𝑑 𝑝)
• Example : Let P=([3], ≤ 𝑃) be the usual chain order and Q=([2], ≤ 𝑄) be the
anti chain order. If [3]×[2], then the R-sum is the Y order:
1
2
3
4
(4-3)
5
(5-3)