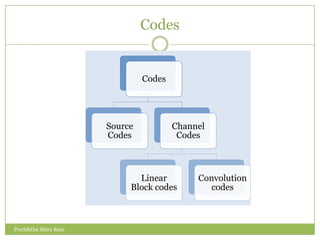
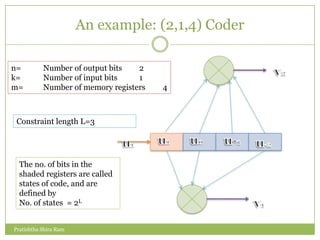
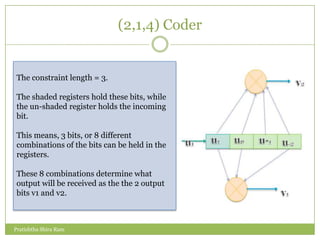
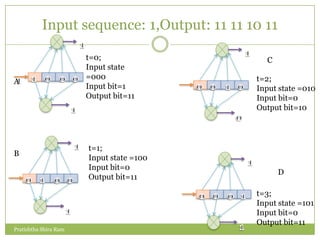
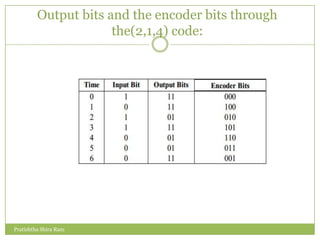
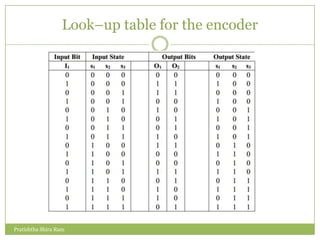
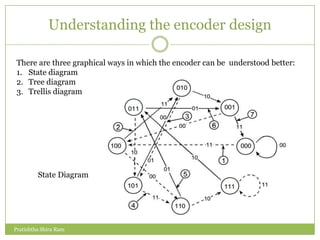
The document discusses convolution codes. It defines convolution codes as having three parameters (n, k, m) where n is the number of output bits, k is the number of input bits, and m is the number of memory registers. Convolutional codes add redundancy to protect data sent over noisy channels and are characterized by their constraint length L, which represents the number of bits in the encoder memory affecting output. The document provides an example of a (2,1,4) convolutional code and illustrates its operation through input sequences, state diagrams, tree diagrams, and trellis diagrams. It also describes methods for decoding convolution codes including sequential decoding using the Fano algorithm and maximum likelihood decoding using the Viterbi algorithm.

1. Convolution Codes
ADVANCED COMMUNICATION SYSTEMS
PRATISHTHA SHIRA RAM
SEMESTER 8
DEPT. OF ECE
Pratishtha Shira Ram

2. Codes
Codes
Source Channel
Codes Codes
Linear Convolution
Block codes codes
Pratishtha Shira Ram

3. Codes (contd.)
1 Source Codes
• The aim of source coding is to take the
source data and make it smaller.
2 Channel Codes
• The aim of channel coding theory is to
find codes which transmit
quickly, contain many valid code words
and can correct or at least detect many
errors.
Pratishtha Shira Ram

4. Channel Codes
Channel codes are used to add redundancy to the codes.
Redundancy adds extra information about the data into the signal.
This extra information ensures that the data is received correctly at the
information sink.
Hence, channel codes increase the BER of the signal.
The aim of channel coding
The channel code is used to theory is to find codes which
protect data sent over it for transmit quickly, contain
storage or retrieval even in the many valid code words and
presence of noise (errors). can correct or at least detect
many errors.
Pratishtha Shira Ram

5. Convolution Codes
Convolutional codes are characterized by
thee parameters:
(n, k, m)
Where,
n= Number of output bits
k= Number of input bits
m= Number of memory registers
Code Rate = k/n
=Number of input bits
/Number of output bits
Constraint length “L”= k(m-1)
L represents the no. of bits in the encoder
memory that affects the generation of n
output bits
Pratishtha Shira Ram

6. An example: (2,1,4) Coder
n= Number of output bits 2
k= Number of input bits 1
m= Number of memory registers 4
Constraint length L=3
The no. of bits in the
shaded registers are called
states of code, and are
defined by
No. of states = 2L
Pratishtha Shira Ram

7. (2,1,4) Coder
The constraint length = 3.
The shaded registers hold these bits, while
the un-shaded register holds the incoming
bit.
This means, 3 bits, or 8 different
combinations of the bits can be held in the
registers.
These 8 combinations determine what
output will be received as the the 2 output
bits v1 and v2.
Pratishtha Shira Ram

8. Input sequence: 1,Output: 11 11 10 11
t=0; C
Input state
=000 t=2;
A
Input bit=1 Input state =010
Output bit=11 Input bit=0
Output bit=10
t=1;
B
Input state =100
Input bit=0
D
Output bit=11
t=3;
Input state =101
Input bit=0
Output bit=11
Pratishtha Shira Ram

9. The convolution
Providing input of 1 to the coder provides what is called the ”impulse response”
of that coder.
Here, providing 1 as input (and then „flushing‟ it out from the registers using
zeros) gave the output sequence : 11 11 10 11.
Similarly, response for input bit 0 would be : 00 00 00 00.
The output sequence can be computed simply by convolving the input sequence
u with the impulse response g.
Or,
v=u*g
By the principle of linear superposition, a coded sequence can be generated
from the impulse response.
Pratishtha Shira Ram

10. Example
To find the coded sequence for the input 1011, we just have to add the shifted
versions of the individual responses:
Input bit Its Impulse Response
1 11 11 10 11
0 00 00 00 00
1 11 11 10 11
1 11 11 10 11
1011 11 11 01 11 01 01 11
This result can be verified by the encoder model too.
Pratishtha Shira Ram

11. Output bits and the encoder bits through
the(2,1,4) code:
Pratishtha Shira Ram

12. Look–up table for the encoder
Pratishtha Shira Ram

13. Understanding the encoder design
There are three graphical ways in which the encoder can be understood better:
1. State diagram
2. Tree diagram
3. Trellis diagram
State Diagram
Pratishtha Shira Ram

14. Tree Diagram
Pratishtha Shira Ram

15. Trellis Diagram
Pratishtha Shira Ram

16. Trellis Diagram –Encoded Sequence
Pratishtha Shira Ram

17. Deconvolution of codes
There are 2 basic methods of deconvolution
1. Sequential decoding: Fano algorithm
- It allows both forward and backward movement through the Trellis diagram
flow.
-If instead of 11 11 01 11 01 01 11, the code 01 11 01 11 01 01 11 is
received, the algorithm will take a start and tally with the outputs it finds on the
way. If an output does not tally, it retraces its position back to the previous
ambiguous decision.
2. Maximum –Likelihood decoding: Viterbi algorithm
-The viterbi decoder examines the entire received sequence of a given length.
-The decoder then computes a metric for the path and then makes a decision
based on it.
-The path with the higher metric is kept, and the one with the lower one is
discarded.
- Generally the Hamming distance is used as the metric here.
Pratishtha Shira Ram

18. Sequential decoding: Fano algorithm
Pratishtha Shira Ram

19. Maximum –Likelihood decoding:
Viterbi algorithm [Step 1]
Pratishtha Shira Ram

20. Maximum –Likelihood decoding:
Viterbi algorithm [Step 2]
Pratishtha Shira Ram

21. Maximum –Likelihood decoding:
Viterbi algorithm [Step 3]
Pratishtha Shira Ram

22. Maximum –Likelihood decoding:
Viterbi algorithm [Step 4]
Pratishtha Shira Ram

23. Thank you!
Pratishtha Shira Ram